Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T09:44:15.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois groups associated with CM-fields, skew-symmetric matrices and orthogonal matrices

Published online by Cambridge University Press:  18 May 2009

S. D. Cohen  and
R. W. K. Odoni
S. D. Cohen
Affiliation:
Department of MathematicsUniversity of Glasgow GlasgowG12 8QW
R. W. K. Odoni
Affiliation:
Department of MathematicsUniversity of Exeter ExeterEx4 4QJ
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main aims of this paper are to provide a device for constructing large families of complex-multiplication (CM) fields, and to examine the Galois groups of some related field extensions. We recall that an algebraic number field K (i.e. 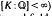) is called a CM-field if it is totally complex but is quadratic over some totally real field (see Section 1). CM fields are important in algebraic geomety, since the ring of endomorphisms of a simple abelian variety defined over an algebraic number field is either ℤ or a ℤ-order in a CM field. Moreover, CM fields figure prominently in classfield theory, since Shimura [15] has shown that “almost all” classfields over CM fields K can be generated by means of division points on abelian varieties admitting ℤ-orders in K as their endomorphism rings. Shimura's work can be regarded as a natural generalization of the classical method (due to Kronecker and H. Weber) of generating classfields of imaginary quadratic fields via division points on CM-elliptic curves.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 1 , January 1990 , pp. 35 - 46
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Bender, E. A., Characteristic polynomials of symmetric matrices, Pacific J. Math. 25 (1968), 433–441.CrossRefGoogle Scholar
2.Burnside, W., Theory of Groups of Finite Order (2nd edition) (Dover Publs. Inc., 1955).Google Scholar
3.Cohen, S. D., The Distribution of the Galois groups of integral polynomials, Illinois J. Math. 23 (1979), 135–152.CrossRefGoogle Scholar
4.Cohen, S. D., The Galois group of a polynomial with two indeterminate coefficients, Pacific J. Math. 90 (1980), 63–76; 97 (1981), 482–486.CrossRefGoogle Scholar
5.Cohen, S. D. and Stothers, W. W., The Galois group of f(x r), Glasgow Math. J. 25 (1984), 75–91.CrossRefGoogle Scholar
6.Fried, M., Fields of definition of function fields and Hurwitz Families; Group as Galois groups, Comm. Algebra 5 (1977), 17–82.CrossRefGoogle Scholar
7.Fried, M., Galois groups and complex multiplication, Trans. Amer. Math. Soc. 235 (1978), 141–163.CrossRefGoogle Scholar
8.Jacobson, N., Basic Algebra (in 2 volumes) (1st edition) (W. H. Freeman and Co., 1974, 1980).Google Scholar
9.Krakowski, F., Eigenwerte und Minimalpolynome symmetrischer Matrizen in kommutativen Korpern, Comm. Math. Helv. 32 (1958), 224–240.CrossRefGoogle Scholar
10.Lang, S., Complex Multiplication, (Grundlehren der mathematischen Wissenschaften 255, Springer-Verlag, 1983).CrossRefGoogle Scholar
11.Lang, S., Fundamentals of Diophantine Geometry, (Springer-Verlag, 1983).CrossRefGoogle Scholar
12.Odoni, R. W. K., The Galois theory of iterates and composites of polynomials, Proc. London Math. Soc. (3), 51 (1985), 385–414.CrossRefGoogle Scholar
13.Osada, H., The Galois groups of the polynomials x n + ax 1 + b, J. Number Theory 25 (1987), 230–238.CrossRefGoogle Scholar
14.Osada, H., The Galois group of the polynomials x n + ax 5 + b, II, Tôhoku Math J. 39 (1987), 437–445.CrossRefGoogle Scholar
15.Shimura, G., Introduction to the arithmetic theory of automorphic functions, (Princeton, Univ. Press, 1971).Google Scholar