Hostname: page-component-7bb8b95d7b-cx56b Total loading time: 0 Render date: 2024-09-20T19:18:05.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois representations of superelliptic curves

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  24 November 2022

Ariel Pacetti Open the ORCID record for Ariel Pacetti [Opens in a new window]  and
Angel Villanueva
Ariel Pacetti*
Affiliation:
Department of Mathematics, Center for Research and Development in Mathematics and Applications (CIDMA), University of Aveiro, 3810-193 Aveiro, Portugal
Angel Villanueva
Affiliation:
FAMAF-CIEM, Universidad Nacional de Córdoba, C.P: 5000 Córdoba, Argentina
*
*Corresponding author. E-mail: apacetti@ua.pt
Get access Rights & Permissions [Opens in a new window]

Abstract

A superelliptic curve over a discrete valuation ring 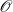$\mathscr{O}$ of residual characteristic p is a curve given by an equation 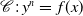$\mathscr{C}\;:\; y^n=\,f(x)$, with 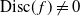$\textrm{Disc}(\,f)\neq 0$. The purpose of this article is to describe the Galois representation attached to such a curve under the hypothesis that f(x) has all its roots in the fraction field of 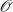$\mathscr{O}$ and that 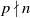$p \nmid n$. Our results are inspired on the algorithm given in Bouw and WewersGlasg (Math. J. 59(1) (2017), 77–108.) but our description is given in terms of a cluster picture as defined in Dokchitser et al. (Algebraic curves and their applications, Contemporary Mathematics, vol. 724 (American Mathematical Society, Providence, RI, 2019), 73–135.).

Keywords

Superelliptic CurvesGalois representations

MSC classification

Primary: 11G20: Curves over finite and local fields
Secondary: 11F80: Galois representations
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 2 , May 2023 , pp. 356 - 382
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Best, A. J., Alexander Betts, L., Bisatt, M., van Bommel, R., Dokchitser, V., Faraggi, O., Kunzweiler, S., Maistret, C., Morgan, A., Muselli, S. and Nowell, S., A user’s guide to the local arithmetic of hyperelliptic curves (2020). arXiv:2007.01749.Google Scholar
Bouw, I. I., Koutsianas, A., Sijsling, J. and Wewers, S., Conductor and discriminant of Picard curves, J. Lond. Math. Soc. (2) 102(1) (2020), 368–404.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 21 (Springer-Verlag, Berlin, 1990).CrossRefGoogle Scholar
Bouw, I. I. and Wewers, S., Computing L-functions and semistable reduction of superelliptic curves, Glasg. Math. J. 59(1) (2017), 77–108.CrossRefGoogle Scholar
Coates, J., Fukaya, T., Kato, K. and Sujatha, R., Root numbers, Selmer groups, and non-commutative Iwasawa theory, J. Algebraic Geom. 19(1) (2010), 19–97.CrossRefGoogle Scholar
Dokchitser, T., Models of curves over discrete valuation rings, Duke Math. J. 170(11) (2021), 2519–2574.CrossRefGoogle Scholar
Dokchitser, T. and Dokchitser, V., Local galois representations and frobenius traces (2022), arxiv:2201.04094.Google Scholar
Dokchitser, T., Dokchitser, V., Maistret, C. and Morgan, A., Semistable types of hyperelliptic curves, in Algebraic curves and their applications, Contemporary Mathematics, vol. 724 (American Mathematical Society, Providence, RI, 2019), 73–135.CrossRefGoogle Scholar
Dokchitser, T., Dokchitser, V. and Morgan, A., Tate module and bad reduction, Proc. Am. Math. Soc. 149(4) (2021), 1361–1372.CrossRefGoogle Scholar
Grothendieck, A., Groupes de monodromie en Géometrie Algégrique SGA 7I), Lecture Notes in Mathematics, vol. 288 (Springer-Verlag, 1972).Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer-Verlag, New York-Heidelberg, 1977).10.1007/978-1-4757-3849-0CrossRefGoogle Scholar
Kani, E., Relations between the genera and between the Hasse-Witt invariants of Galois coverings of curves, Canad. Math. Bull. 28(3) (1985), 321–327.CrossRefGoogle Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, vol. 6 (Oxford University Press, Oxford, 2002). Translated from the French by Reinie Erné, Oxford Science Publications.Google Scholar
Silverman, J. H., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 151 (Springer-Verlag, New York, 1994).CrossRefGoogle Scholar
Sutherland, A. V., Counting points on superelliptic curves in average polynomial time, in ANTS XIV—proceedings of the fourteenth algorithmic number theory symposium, Open Book Series, vol. 4 (Mathematical Sciences Publishers, Berkeley, CA, 2020), 403–422.CrossRefGoogle Scholar