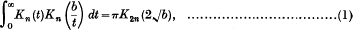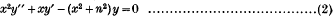Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ragab, Fouad M.
1953.
An Integral involving a Modified Bessel Function of the Second Kind and an E-function.
Proceedings of the Glasgow Mathematical Association,
Vol. 1,
Issue. 3,
p.
119.