Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guralnick, Robert M.
1984.
Generation of the lower central series II.
Glasgow Mathematical Journal,
Vol. 25,
Issue. 2,
p.
193.
Kaushik, Rahul
and
Yadav, Manoj K.
2021.
Commutators and commutator subgroups of finite p-groups.
Journal of Algebra,
Vol. 568,
Issue. ,
p.
314.

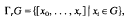
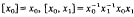 , and for
, and for