Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T07:08:59.127Z Has data issue: false hasContentIssue false
  • English
  • Français

GOLDIE RANK OF PRIMITIVE QUOTIENTS VIA LATTICE POINT ENUMERATION

Published online by Cambridge University Press:  01 October 2013

JOANNA MEINEL  and
CATHARINA STROPPEL
JOANNA MEINEL
Affiliation:
Department of Mathematics, Endenicher Allee 60, 53115 Bonn E-mail: stroppel@math.uni-bonn.de; joanna.meinel@uni-bonn.de
CATHARINA STROPPEL
Affiliation:
Department of Mathematics, Endenicher Allee 60, 53115 Bonn E-mail: stroppel@math.uni-bonn.de; joanna.meinel@uni-bonn.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be an algebraically closed field of characteristic zero. I. M. Musson and M. Van den Bergh (Mem. Amer. Math. Soc., vol. 136, 1998, p. 650) classify primitive ideals for rings of torus invariant differential operators. This classification applies in particular to subquotients of localized extended Weyl algebras 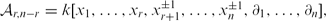$\mathcal{A}_{r,n-r}=k[x_1,\ldots,x_r,x_{r+1}^{\pm1}, \ldots, x_{n}^{\pm1},\partial_1,\ldots,\partial_n],$ where it can be made explicit in terms of convex geometry. We recall these results and then turn to the corresponding primitive quotients and study their Goldie ranks. We prove that the primitive quotients fall into finitely many families whose Goldie ranks are given by a common quasi-polynomial and then realize these quasi-polynomials as Ehrhart quasi-polynomials arising from convex geometry.

Keywords

17B1016S3252B20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue A: New developments in Noncommutative Algebra and its applications. A conference in honour of Kenny Brown's and Toby Stafford's 60th birthdays. , October 2013 , pp. 149 - 168
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Barvinok, A. and Pommersheim, J. E., An algorithmic theory of lattice points in polyhedra, New Perspectives in Algebraic Combinatorics, vol. 38 (Cambridge University Press, Cambridge, UK, 1999), 91–147.Google Scholar
2.Beck, M. and Robins, S., Computing the continuous discretely: Integer-point enumeration in polyhedra, Undergraduate Texts in Mathematics (Springer, New York, 2007).Google Scholar
3.Braden, T., Licata, A., Proudfoot, N. and Webster, B., Hypertoric category ${\cal O}$, Adv. Math. 231 (3–4) (2012), 1487–1545.Google Scholar
4.Brundan, J., Mœglin's theorem and Goldie rank polynomials in Cartan type A, Compos. Math. 147 (6) (2011), 1741–1771.CrossRefGoogle Scholar
5.Coutinho, S. C., A primer of algebraic D-modules, London Mathematical Society Student Texts, vol. 33 (Cambridge University Press, Cambridge, UK, 1995).Google Scholar
6.Duflo, M., Sur la classification des idéaux primitifs dans l'algèbre enveloppante d'une algèbre de Lie semi-simple, Ann. Math. (2) 105 (1) (1977), 107–120.CrossRefGoogle Scholar
7.Ehrhart, E., Sur les polyèdres rationnels homothétiques à n dimensions, C. R. Acad. Sci. Paris 254 (1962), 616–618.Google Scholar
8.Jantzen, J.-C., Einhüllende Algebren halbeinfacher Lie-Algebren, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 3 (Springer, Berlin, 1983).Google Scholar
9.Joseph, A., Goldie rank in the enveloping algebra of a semisimple Lie algebra. I, II, J. Algebra 65 (2) (1980), 269–283; 284–306.Google Scholar
10.Joseph, A., Primitive ideals in enveloping algebras, Proceedings of the International Congress of Mathematicians, Warsaw, vol. 1, 2 (Warsaw: PWN), 1984, pp. 403–414.Google Scholar
11.Lam, T. Y., A first course in noncommutative rings, Graduate Texts in Mathematics, vol. 131 (Springer, New York, 1991).Google Scholar
12.Lam, T. Y., Lectures on modules and rings, Graduate Texts in Mathematics, vol. 189 (Springer, New York, 1999).Google Scholar
13.Linke, E., Rational Ehrhart quasi-polynomials, J. Comb. Theory Series A 118 (2011), 1966–1978.Google Scholar
14.Meinel, J., Die Beschreibung primitiver Ideale durch Hyperebenen und Gitterpunkte, Diploma thesis (University of Bonn, 2011).Google Scholar
15.Musson, I. M. and Van den Bergh, M., Invariants under tori of rings of differential operators and related topics, Mem. Amer. Math. Soc. 136 (1998), no. 650.Google Scholar
16.Premet, A., Enveloping algebras of Slodowy slices and Goldie rank, Transform. Groups 16 (2011), 857–888.Google Scholar
17.Ziegler, G. M., Lectures on polytopes, Graduate Texts in Mathematics, vol. 152 (Springer, New York, 1995).Google Scholar