Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T07:02:39.030Z Has data issue: false hasContentIssue false
  • English
  • Français

GORENSTEIN MODULES AND GORENSTEIN MODEL STRUCTURES

Part of: Homological algebra

Published online by Cambridge University Press:  27 February 2017

AIMIN XU
AIMIN XU*
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu 273165, China e-mail: xuaimin88888@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a complete hereditary cotorsion pair 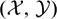$(\mathcal{X}, \mathcal{Y})$, we introduce the concept of 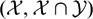$(\mathcal{X}, \mathcal{X} \cap \mathcal{Y})$-Gorenstein projective modules and study its stability properties. As applications, we first get two model structures related to Gorenstein flat modules over a right coherent ring. Secondly, for any non-negative integer n, we construct a cofibrantly generated model structure on Mod(R) in which the class of fibrant objects are the modules of Gorenstein injective dimension ≤ n over a left Noetherian ring R. Similarly, if R is a left coherent ring in which all flat left R-modules have finite projective dimension, then there is a cofibrantly generated model structure on Mod(R) such that the cofibrant objects are the modules of Gorenstein projective dimension ≤ n. These structures have their analogous in the category of chain complexes.

MSC classification

Primary: 18G25: Relative homological algebra, projective classes
Secondary: 18G10: Resolutions; derived functors
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 685 - 703
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Asadollahi, J. and Salarian, Sh., Cohomology theories based on flats, J. Algebra 353 (2012), 93–120.Google Scholar
2. Beligiannis, A. and Reiten, I., Homological and homotopical aspects of torsion theories, Mem. Amer. Math. Soc. 188, 2007.Google Scholar
3. Bennis, D., Weak Gorenstein global dimension, Int. Electron. J. Algebra. 8 (2010), 140–152.Google Scholar
4. Bennis, D. and Mahdou, N., Global Gorenstein dimensions, Proc. Amer. Math. Soc. 138 (2) (2010), 461–465.Google Scholar
5. Bravo, D. and Gillespie, J., Absolutely clean, level, and Gorenstein AC-injective complexes, Comm. Algebra 44 (5) (2016), 2213–2233.Google Scholar
6. Bravo, D., Gillespie, J. and Hovey, M., The stable module category of a general ring, arXiv:1405.5768v1, 2014.Google Scholar
7. Christensen, L. W., Frankild, A. and Holm, H., On Gorenstein projective, injective and flat dimensions-A functorial description with applications, J. Algebra 302 (2006), 231–279.CrossRefGoogle Scholar
8. Cortés Izurdiaga, M. and Guil Asensio, P. A., A Quillen model structure approach to the finitistic dimension conjectures, Math. Scand. 285 (7) (2012), 821–833.Google Scholar
9. Ding, N. and Chen, J., Coherent rings with finite self-FP-injective dimension, Comm. Algebra 24 (1996), 2963–2980.CrossRefGoogle Scholar
10. Ding, N. and Chen, J., The flat dimensions of injective modules, Manuscripta Math. 78 (2) (1993), 165–177.Google Scholar
11. Enochs, E. E., Estrada, S. and García Rozas, J. R., Gorenstein categories and Tate cohomology on projective schemes, Math. Nachr. 281 (4) (2008), 525–540.Google Scholar
12. Enochs, E. E. and Jenda, O. M. G., Relative homological algebra (Walter de Gruyter, Berlin, New York, 2000).Google Scholar
13. Enochs, E. E., Jenda, O. M. G. and Lopez-Ramos, J. A., The existence of Gorenstein flat covers, Math. Scand. 94 (1) (2004), 46–62.CrossRefGoogle Scholar
14. García Rozas, J. R., Covers and envelopes in the category of complexes of modules (BocaRaton, London, 1999).Google Scholar
15. Gillespie, J., How to construct a Hovey triple from two cotorsion pairs, preprint; arXiv:1406.2619, 2014.Google Scholar
16. Gillespie, J., Model structures on modules over Ding-Chen rings, Homology, Homotopy Appl. 12 (1) (2010), 61–73.Google Scholar
17. Gillespie, J., The flat model structure on Ch(R), Tran. Amer. Math. Soc. 356 (8) (2004), 3369–3390.CrossRefGoogle Scholar
18. Gillespie, J., The flat stable module category of a coherent ring, arXiv:1412.4085v1, 2014.Google Scholar
19. Gillespie, J. and Hovey, M., Gorenstein model structures and generalized derived categories, Proc. Edinburgh Math. Soc. 53 (2010), 675–696.Google Scholar
20. Göbel, R. and Trlifaj, J., Approximations and endomorphism algebras of modules, GEM 41 (Walter de Gruyter, Berlin, New York, 2006).CrossRefGoogle Scholar
21. Hashimoto, M., Auslander-Buchweitz Approximations of Equivariant Modules, London Mathematical Society Lecture Note Series, vol. 282 (Cambridge University Press, Cambridge, 2000).Google Scholar
22. Holm, H., Gorenstein homological dimensions, J. Pure Appl. Algebra 189 (1–3) (2004), 167–193.Google Scholar
23. Hovey, M., Cotorsion pairs, model category structures, and representation theory, Math. Z. 241 (2002), 553–592.Google Scholar
24. Hovey, M., Cotorsion pairs and model categories, in Interactions between homotopy theory and algebra, Contemporary Mathematics, vol. 436 (Angeleri Hügel, L., Happel, D. and Krause, H., Editors) (American Mathematics Society, Providences, RI, 2007), 277–296.Google Scholar
25. Marco, A. and Pérez, B., Gorenstein homological dimensions and Abelian model structures, arxiv:1212.1517v3, 2014.Google Scholar
26. Pan, Q. X. and Cai, F. Q., $(\mathcal{X}, \mathcal{Y})$ -Gorenstein projective and injective modules, Turk. J. Math. 39 (2015), 81–90.Google Scholar
27. Rotman, J. J., An introduction to homological algebra (Academic Press, New York, 1979).Google Scholar
28. Salce, L., Cotorsion theories for abelian groups, Symposia Math. 23 (1979), 11–32.Google Scholar
29. Sather-Wagstaff, S., Sharif, T. and White, D., Stability of Gorenstein categories, J. London Math. Soc. 77 (2008), 481–502.Google Scholar
30. Sather-Wagstaff, S., Sharif, T. and White, D., AB-contexts and stability for Gorenstein flat modules with respect to semidualizing modules, Algebr. Represent. Theory 14 (2011), 403–428.CrossRefGoogle Scholar
31. Trlifaj, J., Infinite dimensional tilting modules and cotorsion pairs, in Handbook of tilting theory, London Math. Soc. Lecture Note Ser., vol. 332 (Avramov, L. L., Christensen, J. D., Dwyer, W. G., Mandell, M. A. and Shipley, B. E., Editors) (Cambridge University Press, Cambridge, UK, 2007) 279–321.Google Scholar
32. Yang, C. H. and Liang, L., Gorenstein injective and projective complexes with respect to a semidualizing module, Comm. Algebra 40 (2012), 3352–3364.Google Scholar
33. Yang, X. Y. and Liu, Z. K., Gorenstein projective, injective, and flat complexes, Comm. Algebra 39 (2011), 1705–1721.Google Scholar
34. Yang, G. and Liu, Z. K., Stability of Gorenstein flat categories, Glasgow Math. J. 54 (1) (2012), 177–191.Google Scholar
35. Xu, J. Z., Flat covers of modules, Lecture Notes in Mathematics, vol. 1634 (Springer-Verlag, Berlin, 1996).Google Scholar
36. Zhu, X. S., The homological theory of quasi-resolving subcategories, J. Algebra 414 (2014), 6–40.Google Scholar