Hereditary semisimple classes

Extract

It is well-known (see e.g. [1, p. 5]) that a class ℳ of (not necessarily associative) rings is the semisimple class for some radical class, relative to some universal class 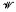if and only if it has the following properties:

(a)if ℳ, then every non-zero ideal I of Rhas a non-zero homomorphic image I/J∈ℳ.

(b) If R∈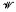 but R∉ℳ, then R has a non-zero ideal I∈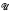, where 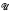ℳ = {K ∈ 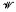| every non-zero K/H∉ℳ}. In fact 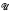ℳ is the radical class whose semisimple class is ℳ. On the other hand, if ℘ is a radical class, then ℐ℘ = {K∈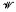/ if I is a non-zero ideal of K, then I∉℘} is its semisimple class. If a class ℳ is hereditary (that is, when R∈ℳ, then all its ideals are in ℳ), it clearly satisfies (a), but there do exist non-hereditary semisimple classes (see [2]). The condition (satisfied in all associative or alternative classes) is that 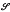℘ is hereditary for a radical class ℘ if and only if ℘(I) ⊆ ℘(R) for all ideals I of all rings R∈ 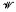[3, Lemma 2, p. 595].