Published online by Cambridge University Press: 27 October 2021
Let 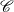 $\mathscr{C}$
be a
$\mathscr{C}$
be a 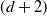 $(d+2)$
-angulated category with d-suspension functor
$(d+2)$
-angulated category with d-suspension functor 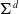 $\Sigma^d$
. Our main results show that every Serre functor on
$\Sigma^d$
. Our main results show that every Serre functor on 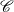 $\mathscr{C}$
is a
$\mathscr{C}$
is a 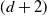 $(d+2)$
-angulated functor. We also show that
$(d+2)$
-angulated functor. We also show that 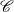 $\mathscr{C}$
has a Serre functor
$\mathscr{C}$
has a Serre functor 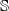 $\mathbb{S}$
if and only if
$\mathbb{S}$
if and only if 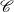 $\mathscr{C}$
has Auslander–Reiten
$\mathscr{C}$
has Auslander–Reiten 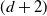 $(d+2)$
-angles. Moreover,
$(d+2)$
-angles. Moreover, 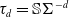 $\tau_d=\mathbb{S}\Sigma^{-d}$
where
$\tau_d=\mathbb{S}\Sigma^{-d}$
where 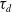 $\tau_d$
is d-Auslander–Reiten translation. These results generalize work by Bondal–Kapranov and Reiten–Van den Bergh. As an application, we prove that for a strongly functorially finite subcategory
$\tau_d$
is d-Auslander–Reiten translation. These results generalize work by Bondal–Kapranov and Reiten–Van den Bergh. As an application, we prove that for a strongly functorially finite subcategory  $\mathscr{X}$
of
$\mathscr{X}$
of 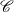 $\mathscr{C}$
, the quotient category
$\mathscr{C}$
, the quotient category 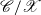 $\mathscr{C}/\mathscr{X}$
is a
$\mathscr{C}/\mathscr{X}$
is a 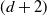 $(d+2)$
-angulated category if and only if
$(d+2)$
-angulated category if and only if 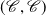 $(\mathscr{C},\mathscr{C})$
is an
$(\mathscr{C},\mathscr{C})$
is an 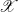 $\mathscr{X}$
-mutation pair, and if and only if
$\mathscr{X}$
-mutation pair, and if and only if 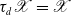 $\tau_d\mathscr{X} =\mathscr{X}$
.
$\tau_d\mathscr{X} =\mathscr{X}$
.
This work was supported by the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 19B239) and the National Natural Science Foundation of China (Grant No. 11901190).