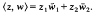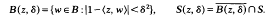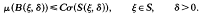Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mochizuki, Nozomu
1986.
Fejér-Riesz inequalities for lower-dimensional subspaces.
Tohoku Mathematical Journal,
Vol. 38,
Issue. 3,
Mochizuki, Nozomu
1988.
Inequalities of Fejér-Riesz and Hardy-Littlewood.
Tohoku Mathematical Journal,
Vol. 40,
Issue. 1,
Choe, Boo Rim
1992.
The essential norms of composition operators.
Glasgow Mathematical Journal,
Vol. 34,
Issue. 2,
p.
143.
Aleksandrov, A. B.
1994.
Several Complex Variables II.
Vol. 8,
Issue. ,
p.
107.
KIM, KYUNGSUP
2005.
A FAST FACTORIZATION ALGORITHM FOR A CONFLUENT CAUCHY MATRIX.
Journal of the Korean Mathematical Society,
Vol. 42,
Issue. 1,
p.
1.
UEKI, SEI-ICHIRO
2005.
COMPOSITION OPERATORS ON THE PRIVALOV SPACES OF THE UNIT BALL OF ℂn.
Journal of the Korean Mathematical Society,
Vol. 42,
Issue. 1,
p.
111.
Ueki, Sei-Ichiro
Luo, Luo
and
Clark, Stephen
2008.
Compact Weighted Composition Operators and Multiplication Operators between Hardy Spaces.
Abstract and Applied Analysis,
Vol. 2008,
Issue. 1,
Stević, Stevo
Ueki, Sei-Ichiro
and
Berezansky, Leonid
2009.
Weighted Composition Operators and Integral‐Type Operators between Weighted Hardy Spaces on the Unit Ball.
Discrete Dynamics in Nature and Society,
Vol. 2009,
Issue. 1,
Sehba, Benoît Florent
and
Engler, Hans
2011.
p‐Carleson Measures for a Class of Hardy‐Orlicz Spaces.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2011,
Issue. 1,
Charpentier, Stéphane
2011.
Composition Operators on Hardy–Orlicz Spaces on the Ball.
Integral Equations and Operator Theory,
Vol. 70,
Issue. 3,
p.
429.
Charpentier, Stéphane
2012.
Essential norm of composition operators on the Hardy space H 1 and the weighted Bergman spaces $${A_{\alpha}^{p}}$$ on the ball.
Archiv der Mathematik,
Vol. 98,
Issue. 4,
p.
327.
Charpentier, Stéphane
and
Sehba, Benoît
2012.
Carleson Measure Theorems for Large Hardy-Orlicz and Bergman-Orlicz Spaces.
Journal of Function Spaces and Applications,
Vol. 2012,
Issue. ,
p.
1.
Choe, Boo Rim
Koo, Hyungwoon
and
Smith, Wayne
2015.
Composition as an integral operator.
Advances in Mathematics,
Vol. 273,
Issue. ,
p.
149.
SEHBA, BENOÎT F.
2018.
-CARLESON MEASURES AND MULTIPLIERS BETWEEN BERGMAN–ORLICZ SPACES OF THE UNIT BALL OF .
Journal of the Australian Mathematical Society,
Vol. 104,
Issue. 1,
p.
63.
Dje, Jean Marcel Tanoh
and
Sehba, Benoît Florent
2021.
Carleson embeddings for Hardy-Orlicz and Bergman-Orlicz spaces of the upper-half plane.
Functiones et Approximatio Commentarii Mathematici,
Vol. 64,
Issue. 2,
Zhou, Lifang
Zhao, Dong
and
Tang, Xiaomin
2024.
Carleson measures and Berezin-type operators on Fock spaces.
Banach Journal of Mathematical Analysis,
Vol. 18,
Issue. 2,

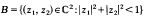 denote the unit ball in ℂ
denote the unit ball in ℂ