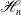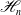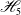1. Introduction and main results
In [Reference Bellamy, Craw, Rayan, Schedler and Weiss5], Bellamy et al introduced a particular family of real hyperplane arrangements in
![]() ${\mathbb R}^n$
stemming from hyperpolygon spaces realized as certain quiver varieties which we call hyperpolygonal arrangements
${\mathbb R}^n$
stemming from hyperpolygon spaces realized as certain quiver varieties which we call hyperpolygonal arrangements
![]() ${\mathscr H}_n$
, see Definition 1.1. In this note, we study these hyperpolygonal arrangements and investigate their properties in a systematic manner. It turns out that the arrangements
${\mathscr H}_n$
, see Definition 1.1. In this note, we study these hyperpolygonal arrangements and investigate their properties in a systematic manner. It turns out that the arrangements
![]() ${\mathscr H}_n$
differentiate essentially between all local properties of arrangements, see Theorem 1.2. In addition, we show that hyperpolygonal arrangements are projectively unique, see Theorem 1.5, and combinatorially formal, see Theorem 1.6.
${\mathscr H}_n$
differentiate essentially between all local properties of arrangements, see Theorem 1.2. In addition, we show that hyperpolygonal arrangements are projectively unique, see Theorem 1.5, and combinatorially formal, see Theorem 1.6.
We briefly indicate how the arrangements
![]() ${\mathscr H}_n$
arise in [Reference Bellamy, Craw, Rayan, Schedler and Weiss5] and show their connection to birational geometry, see [Reference Bellamy, Craw, Rayan, Schedler and Weiss5] for details and references. The arrangement
${\mathscr H}_n$
arise in [Reference Bellamy, Craw, Rayan, Schedler and Weiss5] and show their connection to birational geometry, see [Reference Bellamy, Craw, Rayan, Schedler and Weiss5] for details and references. The arrangement
![]() ${\mathscr H}_n$
characterizes stability conditions on the parameter
${\mathscr H}_n$
characterizes stability conditions on the parameter
![]() $\theta$
of the hyperpolygon space
$\theta$
of the hyperpolygon space
![]() $X_n(\theta )$
. Namely,
$X_n(\theta )$
. Namely,
![]() $X_n(\theta )$
is smooth if and only if
$X_n(\theta )$
is smooth if and only if
![]() $\theta$
does not lie on any hyperplane in
$\theta$
does not lie on any hyperplane in
![]() ${\mathscr H}_n$
. As explained in [Reference Bellamy, Craw, Rayan, Schedler and Weiss5], the varieties
${\mathscr H}_n$
. As explained in [Reference Bellamy, Craw, Rayan, Schedler and Weiss5], the varieties
![]() $X_n(0)$
are conical symplectic varieties and the map
$X_n(0)$
are conical symplectic varieties and the map
![]() $X_n(\theta ) \to X_n(0)$
is a crepant projective resolution (hence a symplectic projective resolution), if
$X_n(\theta ) \to X_n(0)$
is a crepant projective resolution (hence a symplectic projective resolution), if
![]() $\theta$
does not lie in
$\theta$
does not lie in
![]() ${\mathscr H}_n$
. Furthermore, two such resolutions
${\mathscr H}_n$
. Furthermore, two such resolutions
![]() $X_n(\theta _1) \to X_n(0)$
and
$X_n(\theta _1) \to X_n(0)$
and
![]() $X_n(\theta _2) \to X_n(0)$
are isomorphic if
$X_n(\theta _2) \to X_n(0)$
are isomorphic if
![]() $\theta _1$
and
$\theta _1$
and
![]() $\theta _2$
lie in the same region of the complement of
$\theta _2$
lie in the same region of the complement of
![]() ${\mathscr H}_n$
in
${\mathscr H}_n$
in
![]() ${\mathbb R}^n$
. This construction works for all conical symplectic varieties by Namikawa [Reference Namikawa33]: For a conical symplectic variety
${\mathbb R}^n$
. This construction works for all conical symplectic varieties by Namikawa [Reference Namikawa33]: For a conical symplectic variety
![]() $Y$
, there is a certain “parameter space” containing a hyperplane arrangement that characterizes the isomorphism classes of crepant projective resolutions (or, in general, the
$Y$
, there is a certain “parameter space” containing a hyperplane arrangement that characterizes the isomorphism classes of crepant projective resolutions (or, in general, the
![]() $\mathbb Q$
-factorial terminalizations) of
$\mathbb Q$
-factorial terminalizations) of
![]() $Y$
. Very little is known about the hyperplane arrangements arising in this way, although they are essential in understanding the birational geometry of
$Y$
. Very little is known about the hyperplane arrangements arising in this way, although they are essential in understanding the birational geometry of
![]() $Y$
, see also [Reference Bellamy4], [Reference Bellamy, Schedler and Thiel7]. Special cases of conical symplectic varieties are symplectic quotient singularities
$Y$
, see also [Reference Bellamy4], [Reference Bellamy, Schedler and Thiel7]. Special cases of conical symplectic varieties are symplectic quotient singularities
![]() $V/G$
, where
$V/G$
, where
![]() $V$
is a symplectic vector space over
$V$
is a symplectic vector space over
![]() $\mathbb C$
and
$\mathbb C$
and
![]() $G\leq \operatorname {Sp}(V)$
is a finite group maintaining the symplectic form. By [Reference Bellamy, Craw, Rayan, Schedler and Weiss5], the hyperpolygon space
$G\leq \operatorname {Sp}(V)$
is a finite group maintaining the symplectic form. By [Reference Bellamy, Craw, Rayan, Schedler and Weiss5], the hyperpolygon space
![]() $X_n(0)$
is not a quotient singularity for
$X_n(0)$
is not a quotient singularity for
![]() $n \gt 5$
. In contrast,
$n \gt 5$
. In contrast,
![]() $X_4(0)$
is the Kleinian singularity of type
$X_4(0)$
is the Kleinian singularity of type
![]() $D_4$
, that is, the quotient of
$D_4$
, that is, the quotient of
![]() ${\mathbb C}^2$
by the quaternion group
${\mathbb C}^2$
by the quaternion group
![]() $Q_8$
. Further,
$Q_8$
. Further,
![]() $X_5(0)$
is the quotient of
$X_5(0)$
is the quotient of
![]() ${\mathbb C}^4$
by a symplectic reflection group of order 32. This quotient was extensively studied in [Reference Bellamy and Schedler6] and [Reference Donten-Bury and Wiśniewski15].
${\mathbb C}^4$
by a symplectic reflection group of order 32. This quotient was extensively studied in [Reference Bellamy and Schedler6] and [Reference Donten-Bury and Wiśniewski15].
In this note, we study the hyperpolygonal arrangements
![]() ${\mathscr H}_n$
in a systematic manner. We note that
${\mathscr H}_n$
in a systematic manner. We note that
![]() ${\mathscr H}_5$
is the famous counterexample of Edelman and Reiner [Reference Edelman and Reiner17] of Orlik’s conjecture that the restriction of a free arrangement is again free.
${\mathscr H}_5$
is the famous counterexample of Edelman and Reiner [Reference Edelman and Reiner17] of Orlik’s conjecture that the restriction of a free arrangement is again free.
We first recall the definition from [Reference Bellamy, Craw, Rayan, Schedler and Weiss5]. Fix
![]() $n \in {\mathbb N}$
. Let
$n \in {\mathbb N}$
. Let
![]() $V = {\mathbb R}^n$
. Let
$V = {\mathbb R}^n$
. Let
![]() $x_1, \ldots, x_n$
be the dual basis in
$x_1, \ldots, x_n$
be the dual basis in
![]() $V^*$
of the standard
$V^*$
of the standard
![]() $\mathbb R$
-basis of
$\mathbb R$
-basis of
![]() $V$
. For
$V$
. For
![]() $I \subseteq [n] = \{1, \ldots, n\}$
, define the hyperplane
$I \subseteq [n] = \{1, \ldots, n\}$
, define the hyperplane
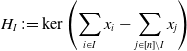 \begin{equation*}H_I\, :\!= \ker \left (\sum _{i \in I}x_i - \sum _{j \in [n]\setminus I}x_j\right ) \end{equation*}
\begin{equation*}H_I\, :\!= \ker \left (\sum _{i \in I}x_i - \sum _{j \in [n]\setminus I}x_j\right ) \end{equation*}
in
![]() $V$
.
$V$
.
Definition 1.1. With the notation as above, the hyperpolygonal arrangement
![]() ${\mathscr H}_n$
in
${\mathscr H}_n$
in
![]() $V$
is defined as
$V$
is defined as
For the various notions used in our main theorem, we refer the reader to Section 2.
Theorem 1.2. Fix
![]() $n \in {\mathbb N}$
. Then we have
$n \in {\mathbb N}$
. Then we have
-
(i)
 ${\mathscr H}_n$
is supersolvable if and only if
${\mathscr H}_n$
is supersolvable if and only if
 $n\le 2$
;
$n\le 2$
; -
(ii)
 ${\mathscr H}_n$
is inductively factored if and only if
${\mathscr H}_n$
is inductively factored if and only if
 $n\le 3$
;
$n\le 3$
; -
(iii)
 ${\mathscr H}_n$
is inductively free if and only if
${\mathscr H}_n$
is inductively free if and only if
 $n\le 4$
;
$n\le 4$
; -
(iv)
 ${\mathscr H}_n$
is free if and only if
${\mathscr H}_n$
is free if and only if
 $n\le 5$
;
$n\le 5$
; -
(v)
 ${\mathscr H}_n$
is simplicial if and only if
${\mathscr H}_n$
is simplicial if and only if
 $n\le 4$
;
$n\le 4$
; -
(vi)
 ${\mathscr H}_n$
is not
${\mathscr H}_n$
is not
 $K(\pi,1)$
if
$K(\pi,1)$
if
 $n\ge 6$
.
$n\ge 6$
.
It follows from Theorem 1.2(v) and Remark 2.19(i) that
![]() ${\mathscr H}_n$
is
${\mathscr H}_n$
is
![]() $K(\pi,1)$
for
$K(\pi,1)$
for
![]() $n \le 4$
and
$n \le 4$
and
![]() ${\mathscr H}_n$
fails to be
${\mathscr H}_n$
fails to be
![]() $K(\pi,1)$
for
$K(\pi,1)$
for
![]() $n \ge 6$
by part (vi). It is not known whether
$n \ge 6$
by part (vi). It is not known whether
![]() ${\mathscr H}_5$
is
${\mathscr H}_5$
is
![]() $K(\pi,1)$
.
$K(\pi,1)$
.
In general,
![]() $K(\pi,1)$
arrangements need not be free, for example see [Reference Orlik and Terao34, Figure 5.4]. However, for hyperpolygonal arrangements, this does seem to be the case. While
$K(\pi,1)$
arrangements need not be free, for example see [Reference Orlik and Terao34, Figure 5.4]. However, for hyperpolygonal arrangements, this does seem to be the case. While
![]() ${\mathscr H}_5$
is free, it is not known whether
${\mathscr H}_5$
is free, it is not known whether
![]() ${\mathscr H}_5$
is
${\mathscr H}_5$
is
![]() $K(\pi,1)$
. We can thus formulate
$K(\pi,1)$
. We can thus formulate
Corollary 1.3. With the possible exception when
![]() $n=5$
,
$n=5$
,
![]() ${\mathscr H}_n$
is
${\mathscr H}_n$
is
![]() $K(\pi,1)$
if and only if
$K(\pi,1)$
if and only if
![]() ${\mathscr H}_n$
is free.
${\mathscr H}_n$
is free.
Thus with the possible exception of
![]() ${\mathscr H}_5$
, the hyperpolygonal arrangements
${\mathscr H}_5$
, the hyperpolygonal arrangements
![]() ${\mathscr H}_n$
satisfy Saito’s Conjecture that for a complexified arrangement freeness implies
${\mathscr H}_n$
satisfy Saito’s Conjecture that for a complexified arrangement freeness implies
![]() $K(\pi,1)$
. Of course, the latter is known to be false in general [Reference Edelman and Reiner18].
$K(\pi,1)$
. Of course, the latter is known to be false in general [Reference Edelman and Reiner18].
Theorem 1.2(ii) and (v) imply the following which is in support of a conjecture due to Falk and Randell namely that every (complex) factored arrangement is
![]() $K(\pi,1)$
, [Reference Falk and Randell22, Probl. 3.12].
$K(\pi,1)$
, [Reference Falk and Randell22, Probl. 3.12].
Corollary 1.4. If
![]() ${\mathscr H}_n$
is factored, then
${\mathscr H}_n$
is factored, then
![]() ${\mathscr H}_n$
is
${\mathscr H}_n$
is
![]() $K(\pi,1)$
.
$K(\pi,1)$
.
A property for arrangements is said to be combinatorial if it only depends on the intersection lattice of the underlying arrangement. In this context, our next theorem shows that the class of hyperpolygonal arrangements is very special in the sense that essentially every property we may formulate for members of this class is combinatorial. This is formally captured by the notion of projective uniqueness due to Ziegler [Reference Ziegler49], see Definition 4.1.
Theorem 1.5. For any
![]() $n \in {\mathbb N}$
,
$n \in {\mathbb N}$
,
![]() ${\mathscr H}_n$
is projectively unique.
${\mathscr H}_n$
is projectively unique.
Theorem 1.5 implies that for the class of all real arrangements whose underlying matroid admits a realization over
![]() $\mathbb R$
as a hyperpolygonal arrangement freeness is combinatorial. In particular, Terao’s conjecture over
$\mathbb R$
as a hyperpolygonal arrangement freeness is combinatorial. In particular, Terao’s conjecture over
![]() $\mathbb R$
is valid within this class, cf. [Reference Ziegler49, Prop. 2.3]. Likewise, asphericity is combinatorial within this class. Whether both these properties are combinatorial in general are longstanding and wide open problems, see [Reference Orlik and Terao34, Conj. 4.138] and [Reference Falk and Randell22, Prob. 3.8].
$\mathbb R$
is valid within this class, cf. [Reference Ziegler49, Prop. 2.3]. Likewise, asphericity is combinatorial within this class. Whether both these properties are combinatorial in general are longstanding and wide open problems, see [Reference Orlik and Terao34, Conj. 4.138] and [Reference Falk and Randell22, Prob. 3.8].
A hyperplane arrangement is called formal provided all linear dependencies among the defining forms of the hyperplanes are generated by ones corresponding to intersections of codimension two. The significance of this notion stems from the fact that complex arrangements with aspherical complements are formal, [Reference Falk and Randell21, Thm. 4.2]. In addition, free arrangements are known to be formal, [Reference Yuzvinsky47, Cor. 2.5], and factored arrangements are formal, [Reference Möller, Mücksch and Röhrle30, Thm. 1.1]. Thus all the properties studied in Theorem 1.2 entail formality. In our next result, we show that indeed all hyperpolygonal arrangements are combinatorially formal, see Definition 5.1.
Theorem 1.6. For any
![]() $n \in {\mathbb N}$
,
$n \in {\mathbb N}$
,
![]() ${\mathscr H}_n$
is combinatorially formal.
${\mathscr H}_n$
is combinatorially formal.
Theorem 1.6 is proved in §5, based on results from [Reference Möller, Mücksch and Röhrle30].
We end in §6 with a brief discussion of the rank-generating functions of the poset of regions of the free hyperpolygonal arrangements
![]() ${\mathscr H}_n$
.
${\mathscr H}_n$
.
For general information about arrangements, we refer the reader to [Reference Orlik and Terao34].
2. Preliminaries
2.1. Hyperplane arrangements
Let
![]() $\mathbb K$
be a field and let
$\mathbb K$
be a field and let
![]() $V = {\mathbb K}^{\ell}$
be an
$V = {\mathbb K}^{\ell}$
be an
![]() ${\ell}$
-dimensional
${\ell}$
-dimensional
![]() $\mathbb K$
-vector space. A hyperplane arrangement is a pair
$\mathbb K$
-vector space. A hyperplane arrangement is a pair
![]() $({\mathscr A}, V)$
, where
$({\mathscr A}, V)$
, where
![]() $\mathscr A{\kern1.5pt}$
is a finite collection of hyperplanes in
$\mathscr A{\kern1.5pt}$
is a finite collection of hyperplanes in
![]() $V$
. Usually, we simply write
$V$
. Usually, we simply write
![]() $\mathscr A{\kern1.5pt}$
in place of
$\mathscr A{\kern1.5pt}$
in place of
![]() $({\mathscr A}, V)$
. By
$({\mathscr A}, V)$
. By
![]() ${\Phi_\ell}$
we denote the empty arrangement in
${\Phi_\ell}$
we denote the empty arrangement in
![]() $V$
.
$V$
.
The lattice
![]() $L({\mathscr A}{\kern1.5pt})$
of
$L({\mathscr A}{\kern1.5pt})$
of
![]() $\mathscr A{\kern1.5pt}$
is the set of subspaces of
$\mathscr A{\kern1.5pt}$
is the set of subspaces of
![]() $V$
of the form
$V$
of the form
![]() $H_1\cap \ldots \cap H_i$
where
$H_1\cap \ldots \cap H_i$
where
![]() $\{ H_1, \ldots, H_i\}$
is a subset of
$\{ H_1, \ldots, H_i\}$
is a subset of
![]() $\mathscr A$
. For
$\mathscr A$
. For
![]() $X \in L({\mathscr A}{\kern1.5pt})$
, we have two associated arrangements, firstly
$X \in L({\mathscr A}{\kern1.5pt})$
, we have two associated arrangements, firstly
![]() ${\mathscr A}_X :\!=\{H \in {\mathscr A} \mid X \subseteq H\} \subseteq {\mathscr A}$
, the localization of
${\mathscr A}_X :\!=\{H \in {\mathscr A} \mid X \subseteq H\} \subseteq {\mathscr A}$
, the localization of
![]() $\mathscr A{\kern1.5pt}$
at
$\mathscr A{\kern1.5pt}$
at
![]() $X$
, and secondly, the restriction of
$X$
, and secondly, the restriction of
![]() $\mathscr A{\kern1.5pt}$
to
$\mathscr A{\kern1.5pt}$
to
![]() $X$
,
$X$
,
![]() $({\mathscr A}^{{\kern1.5pt}X},X)$
, where
$({\mathscr A}^{{\kern1.5pt}X},X)$
, where
![]() ${\mathscr A}^{{\kern1.5pt}X} :\!= \{ X \cap H \mid H \in {\mathscr A} \setminus {\mathscr A}_X\}$
. The lattice
${\mathscr A}^{{\kern1.5pt}X} :\!= \{ X \cap H \mid H \in {\mathscr A} \setminus {\mathscr A}_X\}$
. The lattice
![]() $L({\mathscr A}{\kern1.5pt})$
is a partially ordered set by reverse inclusion:
$L({\mathscr A}{\kern1.5pt})$
is a partially ordered set by reverse inclusion:
![]() $X \le Y$
provided
$X \le Y$
provided
![]() $Y \subseteq X$
for
$Y \subseteq X$
for
![]() $X,Y \in L({\mathscr A}{\kern1.5pt})$
.
$X,Y \in L({\mathscr A}{\kern1.5pt})$
.
A property for arrangements is said to be local if it is passed to every localization of the ambient arrangement. For instance, freeness, asphericity, and factoredness are all local (cf. [Reference Orlik and Terao34, Thm. 4.37], [Reference Paris35, Lem. 1.1], and the proof of [Reference Terao46, Cor. 2.11], respectively). In contrast, this fails for formal arrangements of rank at least 4 (cf. the example following [Reference Yuzvinsky47, Def. 2.3]).
Throughout, we only consider arrangements
![]() $\mathscr A{\kern1.5pt}$
such that
$\mathscr A{\kern1.5pt}$
such that
![]() $0 \in H$
for each
$0 \in H$
for each
![]() $H$
in
$H$
in
![]() $\mathscr A$
. These are called central. In that case the center
$\mathscr A$
. These are called central. In that case the center
![]() $T({\mathscr A}{\kern1.5pt}) :\!= \cap _{H \in {\mathscr A}} H$
of
$T({\mathscr A}{\kern1.5pt}) :\!= \cap _{H \in {\mathscr A}} H$
of
![]() $\mathscr A{\kern1.5pt}$
is the unique maximal element in
$\mathscr A{\kern1.5pt}$
is the unique maximal element in
![]() $L({\mathscr A}{\kern1.5pt})$
with respect to the partial order. A rank function on
$L({\mathscr A}{\kern1.5pt})$
with respect to the partial order. A rank function on
![]() $L({\mathscr A}{\kern1.5pt})$
is given by
$L({\mathscr A}{\kern1.5pt})$
is given by
![]() $r(X) :\!= \operatorname {codim}_V(X)$
. The rank of
$r(X) :\!= \operatorname {codim}_V(X)$
. The rank of
![]() $\mathscr A{\kern1.5pt}$
is defined as
$\mathscr A{\kern1.5pt}$
is defined as
![]() $r({\mathscr A}{\kern1.5pt}) :\!= r(T({\mathscr A}{\kern1.5pt}))$
.
$r({\mathscr A}{\kern1.5pt}) :\!= r(T({\mathscr A}{\kern1.5pt}))$
.
The Poincaré polynomial
![]() $\pi ({\mathscr A},t) \in {\mathbb Z}[t]$
of
$\pi ({\mathscr A},t) \in {\mathbb Z}[t]$
of
![]() $\mathscr A{\kern1.5pt}$
is defined by
$\mathscr A{\kern1.5pt}$
is defined by
and the characteristic polynomial
![]() $\chi ({\mathscr A},t) \in {\mathbb Z}[t]$
of
$\chi ({\mathscr A},t) \in {\mathbb Z}[t]$
of
![]() $\mathscr A{\kern1.5pt}$
is defined by
$\mathscr A{\kern1.5pt}$
is defined by
where
![]() $\mu$
is the Möbius function of
$\mu$
is the Möbius function of
![]() $L({\mathscr A}{\kern1.5pt})$
, see [Reference Orlik and Terao34, Def. 2.48, Def. 2.52].
$L({\mathscr A}{\kern1.5pt})$
, see [Reference Orlik and Terao34, Def. 2.48, Def. 2.52].
We recall the concept of a generic arrangement from [Reference Orlik and Terao34, Def. 5.22].
Definition 2.1. An
![]() $\ell$
-arrangement
$\ell$
-arrangement
![]() $\mathscr A{\kern1.5pt}$
with
$\mathscr A{\kern1.5pt}$
with
![]() ${r}({\mathscr A}{\kern1.5pt})=r$
is called generic if every subarrangement
${r}({\mathscr A}{\kern1.5pt})=r$
is called generic if every subarrangement
![]() $\mathscr B$
of
$\mathscr B$
of
![]() $\mathscr A{\kern1.5pt}$
of cardinality
$\mathscr A{\kern1.5pt}$
of cardinality
![]() $\ell$
is linearly independent and
$\ell$
is linearly independent and
![]() ${|\mathscr A{\kern1.5pt}| \gt r}$
, [Reference Orlik and Terao34, Def. 5.22].
${|\mathscr A{\kern1.5pt}| \gt r}$
, [Reference Orlik and Terao34, Def. 5.22].
2.2. Supersolvable arrangements
Let
![]() $\mathscr A{\kern1.5pt}$
be an arrangement. Following [Reference Orlik and Terao34, §2], we say that
$\mathscr A{\kern1.5pt}$
be an arrangement. Following [Reference Orlik and Terao34, §2], we say that
![]() $X \in L({\mathscr A}{\kern1.5pt})$
is modular provided
$X \in L({\mathscr A}{\kern1.5pt})$
is modular provided
![]() $X + Y \in L({\mathscr A}{\kern1.5pt})$
for every
$X + Y \in L({\mathscr A}{\kern1.5pt})$
for every
![]() $Y \in L({\mathscr A}{\kern1.5pt})$
, cf. [Reference Orlik and Terao34, Def. 2.32, Cor. 2.26]. The following notion is due to Stanley [Reference Stanley42].
$Y \in L({\mathscr A}{\kern1.5pt})$
, cf. [Reference Orlik and Terao34, Def. 2.32, Cor. 2.26]. The following notion is due to Stanley [Reference Stanley42].
Definition 2.2. Let
![]() $\mathscr A{\kern1.5pt}$
be a central (and essential)
$\mathscr A{\kern1.5pt}$
be a central (and essential)
![]() $\ell$
-arrangement. We say that
$\ell$
-arrangement. We say that
![]() $\mathscr A{\kern1.5pt}$
is supersolvable provided there is a maximal chain
$\mathscr A{\kern1.5pt}$
is supersolvable provided there is a maximal chain
of modular elements
![]() $X_i$
in
$X_i$
in
![]() $L({\mathscr A}{\kern1.5pt})$
.
$L({\mathscr A}{\kern1.5pt})$
.
Remark 2.3.
-
(i) By [Reference Orlik and Terao34 , Ex. 2.28],
 $V$
,
$V$
,
 $\{0\}$
and the members in
$\{0\}$
and the members in
 $\mathscr A{\kern1.5pt}$
are always modular in
$\mathscr A{\kern1.5pt}$
are always modular in
 $L({\mathscr A}{\kern1.5pt})$
. It follows that all
$L({\mathscr A}{\kern1.5pt})$
. It follows that all
 $0$
-,
$0$
-,
 $1$
-, and
$1$
-, and
 $2$
-arrangements are supersolvable.
$2$
-arrangements are supersolvable. -
(ii) Supersolvability is a local property [Reference Stanley42 , Prop. 3.2].
2.3. Free arrangements
Free arrangements play a crucial role in the theory of arrangements; see [Reference Orlik and Terao34, §4] for the definition and basic properties. If
![]() $\mathscr A{\kern1.5pt}$
is free, then we can associate with
$\mathscr A{\kern1.5pt}$
is free, then we can associate with
![]() $\mathscr A{\kern1.5pt}$
the multiset of its exponents, denoted
$\mathscr A{\kern1.5pt}$
the multiset of its exponents, denoted
![]() $\exp {\mathscr A}$
.
$\exp {\mathscr A}$
.
Remark 2.4.
-
(i) Generic arrangements are not free, for example see [Reference Rose and Terao39, §4.4].
-
(ii) Freeness is a local property [Reference Orlik and Terao34, Thm. 4.37].
Terao’s Factorization Theorem [Reference Terao44] shows that the Poincaré polynomial of a free arrangement
![]() $\mathscr A{\kern1.5pt}$
factors into linear terms given by the exponents of
$\mathscr A{\kern1.5pt}$
factors into linear terms given by the exponents of
![]() $\mathscr A{\kern1.5pt}$
(cf. [Reference Orlik and Terao34, Thm. 4.137]):
$\mathscr A{\kern1.5pt}$
(cf. [Reference Orlik and Terao34, Thm. 4.137]):
Theorem 2.5. Suppose that
![]() $\mathscr A{\kern1.5pt}$
is free with
$\mathscr A{\kern1.5pt}$
is free with
![]() $\exp {\mathscr A} = \{ b_1, \ldots, b_\ell \}$
. Then
$\exp {\mathscr A} = \{ b_1, \ldots, b_\ell \}$
. Then
Terao’s celebrated Addition-Deletion Theorem [Reference Terao43] plays a fundamental role in the study of free arrangements, [Reference Orlik and Terao34, Thm. 4.51].
Theorem 2.6. Suppose that
![]() ${\mathscr A} \ne \Phi _\ell$
. Let
${\mathscr A} \ne \Phi _\ell$
. Let
![]() ${H_0 \in \mathscr A}$
. Let
${H_0 \in \mathscr A}$
. Let
![]() ${(\mathscr A, \mathscr A{\kern1.5pt}' = \mathscr A \setminus \{H_0\}, \mathscr A{\kern1.5pt}'' = \mathscr A^{{\kern1.5pt}H_0})}$
be a triple of arrangements. Then any two of the following statements imply the third:
${(\mathscr A, \mathscr A{\kern1.5pt}' = \mathscr A \setminus \{H_0\}, \mathscr A{\kern1.5pt}'' = \mathscr A^{{\kern1.5pt}H_0})}$
be a triple of arrangements. Then any two of the following statements imply the third:
-
(i)
 $\mathscr A{\kern1.5pt}$
is free with
$\mathscr A{\kern1.5pt}$
is free with
 $\exp {\mathscr A} = \{ b_1, \ldots, b_{\ell -1}, b_\ell \}$
;
$\exp {\mathscr A} = \{ b_1, \ldots, b_{\ell -1}, b_\ell \}$
; -
(ii)
 ${\mathscr A}{\kern1.5pt}'$
is free with
${\mathscr A}{\kern1.5pt}'$
is free with
 $\exp {\mathscr A}{\kern1.5pt}' = \{ b_1, \ldots, b_{\ell -1}, b_\ell -1\}$
;
$\exp {\mathscr A}{\kern1.5pt}' = \{ b_1, \ldots, b_{\ell -1}, b_\ell -1\}$
; -
(iii)
 ${\mathscr A}{\kern1.5pt}''$
is free with
${\mathscr A}{\kern1.5pt}''$
is free with
 $\exp {\mathscr A}{\kern1.5pt}'' = \{ b_1, \ldots, b_{\ell -1}\}$
.
$\exp {\mathscr A}{\kern1.5pt}'' = \{ b_1, \ldots, b_{\ell -1}\}$
.
Theorem 2.6 motivates the notion of an inductively free arrangement, [Reference Orlik and Terao34, Def. 4.53].
Definition 2.7. The class
![]() $\mathcal{IF}$
of inductively free arrangements is the smallest class of arrangements subject to
$\mathcal{IF}$
of inductively free arrangements is the smallest class of arrangements subject to
-
(i)
 $\Phi _\ell \in {\mathcal{IF}}$
for each
$\Phi _\ell \in {\mathcal{IF}}$
for each
 $\ell \ge 0$
;
$\ell \ge 0$
; -
(ii) if there exists a hyperplane
 $H_0 \in {\mathscr A}$
such that both
$H_0 \in {\mathscr A}$
such that both
 ${\mathscr A}{\kern1.5pt}'$
and
${\mathscr A}{\kern1.5pt}'$
and
 ${\mathscr A}{\kern1.5pt}''$
belong to
${\mathscr A}{\kern1.5pt}''$
belong to
 $\mathcal{IF}$
, and
$\mathcal{IF}$
, and
 $\exp {\mathscr A}{\kern1.5pt} '' \subseteq \exp {\mathscr A}{\kern1.5pt}'$
, then
$\exp {\mathscr A}{\kern1.5pt} '' \subseteq \exp {\mathscr A}{\kern1.5pt}'$
, then
 $\mathscr A{\kern1.5pt}$
also belongs to
$\mathscr A{\kern1.5pt}$
also belongs to
 $\mathcal{IF}$
.
$\mathcal{IF}$
.
Remark 2.8.
-
(i) Inductively free arrangements are free. However, the latter class properly contains the former, cf. [Reference Orlik and Terao34 , Ex. 4.59].
-
(ii) Inductive freeness is also a local property, thanks to [Reference Hoge, Röhrle and Schauenburg26 , Thm 1.1].
-
(iii) Supersolvable arrangements are inductively free, [Reference Orlik and Terao34 , Thm. 4.58].
2.4. Nice arrangements
The notion of a nice or factored arrangement goes back to Terao [Reference Terao46]. It generalizes the concept of a supersolvable arrangement. We recall the relevant notions and results from [Reference Terao46] (cf. [Reference Orlik and Terao34, §2.3]).
Definition 2.9. Let
![]() $\pi = (\pi _1, \ldots, \pi _s)$
be a partition of
$\pi = (\pi _1, \ldots, \pi _s)$
be a partition of
![]() $\mathscr A$
. Then
$\mathscr A$
. Then
![]() $\pi$
is called independent, provided for any choice
$\pi$
is called independent, provided for any choice
![]() $H_i \in \pi _i$
for
$H_i \in \pi _i$
for
![]() $1 \le i \le s$
, the resulting
$1 \le i \le s$
, the resulting
![]() $s$
hyperplanes are linearly independent, that is we have
$s$
hyperplanes are linearly independent, that is we have
![]() $r(H_1 \cap \ldots \cap H_s) = s$
.
$r(H_1 \cap \ldots \cap H_s) = s$
.
Definition 2.10. Let
![]() $\pi = (\pi _1, \ldots, \pi _s)$
be a partition of
$\pi = (\pi _1, \ldots, \pi _s)$
be a partition of
![]() $\mathscr A{\kern1.5pt}$
and let
$\mathscr A{\kern1.5pt}$
and let
![]() $X \in L({\mathscr A}{\kern1.5pt})$
. The induced partition
$X \in L({\mathscr A}{\kern1.5pt})$
. The induced partition
![]() $\pi _X$
of
$\pi _X$
of
![]() ${\mathscr A}_X$
is given by the non-empty blocks of the form
${\mathscr A}_X$
is given by the non-empty blocks of the form
![]() $\pi _i \cap {\mathscr A}_X$
.
$\pi _i \cap {\mathscr A}_X$
.
Definition 2.11. The partition
![]() $\pi$
of
$\pi$
of
![]() $\mathscr A{\kern1.5pt}$
is nice for
$\mathscr A{\kern1.5pt}$
is nice for
![]() $\mathscr A{\kern1.5pt}$
or a factorization of
$\mathscr A{\kern1.5pt}$
or a factorization of
![]() $\mathscr A{\kern1.5pt}$
provided
$\mathscr A{\kern1.5pt}$
provided
-
(i)
 $\pi$
is independent, and
$\pi$
is independent, and -
(ii) for each
 $X \in L({\mathscr A}{\kern1.5pt}) \setminus \{V\}$
, the induced partition
$X \in L({\mathscr A}{\kern1.5pt}) \setminus \{V\}$
, the induced partition
 $\pi _X$
admits a block which is a singleton.
$\pi _X$
admits a block which is a singleton.
If
![]() $\mathscr A{\kern1.5pt}$
admits a factorization, then we also say that
$\mathscr A{\kern1.5pt}$
admits a factorization, then we also say that
![]() $\mathscr A{\kern1.5pt}$
is factored or nice.
$\mathscr A{\kern1.5pt}$
is factored or nice.
Remark 2.12. The class of nice arrangements is closed under taking localizations; cf. the proof of [Reference Terao46 , Cor. 2.11].
In [Reference Terao46, Thm. 2.8], Terao proved that a partition
![]() $\pi$
of
$\pi$
of
![]() $\mathscr A{\kern1.5pt}$
gives rise to a tensor factorization of the Orlik-Solomon algebra of
$\mathscr A{\kern1.5pt}$
gives rise to a tensor factorization of the Orlik-Solomon algebra of
![]() $\mathscr A{\kern1.5pt}$
if and only if
$\mathscr A{\kern1.5pt}$
if and only if
![]() $\pi$
is nice for
$\pi$
is nice for
![]() $\mathscr A$
, see [Reference Orlik and Terao34, Thm. 3.87]. We record a consequence of this fact for our purposes.
$\mathscr A$
, see [Reference Orlik and Terao34, Thm. 3.87]. We record a consequence of this fact for our purposes.
Corollary 2.13. Let
![]() $\pi = (\pi _1, \ldots, \pi _s)$
be a factorization of
$\pi = (\pi _1, \ldots, \pi _s)$
be a factorization of
![]() $\mathscr A$
. Then the following hold:
$\mathscr A$
. Then the following hold:
-
(i)
 $s = r = r({\mathscr A}{\kern1.5pt})$
and
$s = r = r({\mathscr A}{\kern1.5pt})$
and \begin{equation*} \pi ({\mathscr A},t) = \prod _{i=1}^r (1 + |\pi _i|t); \end{equation*}
\begin{equation*} \pi ({\mathscr A},t) = \prod _{i=1}^r (1 + |\pi _i|t); \end{equation*}
-
(ii) the multiset
 $\{|\pi _1|, \ldots, |\pi _r|\}$
only depends on
$\{|\pi _1|, \ldots, |\pi _r|\}$
only depends on
 $\mathscr A$
;
$\mathscr A$
; -
(iii) for any
 $X \in L({\mathscr A}{\kern1.5pt})$
, we have
$X \in L({\mathscr A}{\kern1.5pt})$
, we have \begin{equation*} r(X) = |\{ i \mid \pi _i \cap {\mathscr A}_X \ne \varnothing \}|. \end{equation*}
\begin{equation*} r(X) = |\{ i \mid \pi _i \cap {\mathscr A}_X \ne \varnothing \}|. \end{equation*}
Remark 2.14. It follows from Corollary 2.13 that the question whether
![]() $\mathscr A{\kern1.5pt}$
is factored is a purely combinatorial property and only depends on the lattice
$\mathscr A{\kern1.5pt}$
is factored is a purely combinatorial property and only depends on the lattice
![]() $L({\mathscr A}{\kern1.5pt})$
.
$L({\mathscr A}{\kern1.5pt})$
.
Moreover, the following is immediate from Corollary 2.13 and Theorem 2.5.
Lemma 2.15. Let
![]() $({\mathscr A},\pi )$
be a factored arrangement which is also free. Then
$({\mathscr A},\pi )$
be a factored arrangement which is also free. Then
![]() $\exp {{\mathscr A}} = \{|\pi _1|,\ldots,|\pi _\ell |\}$
.
$\exp {{\mathscr A}} = \{|\pi _1|,\ldots,|\pi _\ell |\}$
.
2.5. Inductively factored arrangements
Following Jambu and Paris [Reference Jambu and Paris27] and Hoge and Röhrle [Reference Hoge and Röhrle24], we introduce further notation. Suppose that
![]() $\mathscr A{\kern1.5pt}$
is non-empty and let
$\mathscr A{\kern1.5pt}$
is non-empty and let
![]() $\pi = (\pi _1, \ldots, \pi _s)$
be a partition of
$\pi = (\pi _1, \ldots, \pi _s)$
be a partition of
![]() $\mathscr A$
. Let
$\mathscr A$
. Let
![]() $H_0 \in \pi _1$
and let
$H_0 \in \pi _1$
and let
![]() $({\mathscr A}, {\mathscr A}{\kern1.5pt}', {\mathscr A}{\kern1.5pt}'')$
be the triple associated with
$({\mathscr A}, {\mathscr A}{\kern1.5pt}', {\mathscr A}{\kern1.5pt}'')$
be the triple associated with
![]() $H_0$
. We have the induced partition
$H_0$
. We have the induced partition
![]() $\pi '$
of
$\pi '$
of
![]() ${\mathscr A}{\kern1.5pt}'$
consisting of the non-empty parts
${\mathscr A}{\kern1.5pt}'$
consisting of the non-empty parts
![]() $\pi _i' :\!= \pi _i \cap {\mathscr A}{\kern1.5pt}'$
. Further, we have the restriction map
$\pi _i' :\!= \pi _i \cap {\mathscr A}{\kern1.5pt}'$
. Further, we have the restriction map
![]() ${\varrho } = {\varrho }_{\pi,H_0} :{\kern1pt} {\mathscr A} \setminus \pi _1 \to {\mathscr A}{\kern1.5pt}''$
given by
${\varrho } = {\varrho }_{\pi,H_0} :{\kern1pt} {\mathscr A} \setminus \pi _1 \to {\mathscr A}{\kern1.5pt}''$
given by
![]() $H \mapsto H \cap H_0$
, depending on
$H \mapsto H \cap H_0$
, depending on
![]() $\pi$
and
$\pi$
and
![]() $H_0$
. Let
$H_0$
. Let
![]() $\pi _i'' :\!= {\varrho }(\pi _i)$
for
$\pi _i'' :\!= {\varrho }(\pi _i)$
for
![]() $i = 2, \ldots, s$
. Clearly, imposing that
$i = 2, \ldots, s$
. Clearly, imposing that
![]() $\pi '' = (\pi ''_2, \ldots, \pi ''_s)$
is again a partition of
$\pi '' = (\pi ''_2, \ldots, \pi ''_s)$
is again a partition of
![]() ${\mathscr A}{\kern1.5pt}''$
entails that
${\mathscr A}{\kern1.5pt}''$
entails that
![]() $\varrho$
is onto.
$\varrho$
is onto.
Here is the analogue for nice arrangements of Terao’s Addition-Deletion Theorem (cf. Theorem 2.6) for free arrangements from [Reference Hoge and Röhrle24].
Theorem 2.16. Suppose
![]() $\pi = (\pi _1, \ldots, \pi _s)$
is a partition of
$\pi = (\pi _1, \ldots, \pi _s)$
is a partition of
![]() ${\mathscr A} \ne \Phi _\ell$
. Let
${\mathscr A} \ne \Phi _\ell$
. Let
![]() $({\mathscr A}, {\mathscr A}{\kern1.5pt}', {\mathscr A}{\kern1.5pt}'')$
be the triple associated with
$({\mathscr A}, {\mathscr A}{\kern1.5pt}', {\mathscr A}{\kern1.5pt}'')$
be the triple associated with
![]() $H_0 \in \pi _1$
. Then any two of the following statements imply the third:
$H_0 \in \pi _1$
. Then any two of the following statements imply the third:
-
(i)
 $\pi$
is nice for
$\pi$
is nice for
 $\mathscr A$
;
$\mathscr A$
; -
(ii)
 $\pi '$
is nice for
$\pi '$
is nice for
 ${\mathscr A}{\kern1.5pt}'$
;
${\mathscr A}{\kern1.5pt}'$
; -
(iii)
 ${\varrho }:{\kern1pt} {\mathscr A} \setminus \pi _1 \to {\mathscr A}{\kern1.5pt}''$
is bijective and
${\varrho }:{\kern1pt} {\mathscr A} \setminus \pi _1 \to {\mathscr A}{\kern1.5pt}''$
is bijective and
 $\pi ''$
is nice for
$\pi ''$
is nice for
 ${\mathscr A}{\kern1.5pt}''$
.
${\mathscr A}{\kern1.5pt}''$
.
The Addition-Deletion Theorem 2.16 for nice arrangements motivates the following stronger notion of factorization, cf. [Reference Jambu and Paris27].
Definition 2.17 [Reference Hoge and Röhrle24, Def. 3.8]. The class
![]() $\mathcal{IF\!AC}$
of inductively factored arrangements is the smallest class of pairs
$\mathcal{IF\!AC}$
of inductively factored arrangements is the smallest class of pairs
![]() $({\mathscr A}, \pi )$
of arrangements
$({\mathscr A}, \pi )$
of arrangements
![]() $\mathscr A{\kern1.5pt}$
along with a partition
$\mathscr A{\kern1.5pt}$
along with a partition
![]() $\pi$
subject to
$\pi$
subject to
-
(i)
 $(\Phi _\ell, (\varnothing )) \in {\mathcal{IF\!AC}}$
for each
$(\Phi _\ell, (\varnothing )) \in {\mathcal{IF\!AC}}$
for each
 $\ell \ge 0$
;
$\ell \ge 0$
; -
(ii) if there exists a partition
 $\pi$
of
$\pi$
of
 $\mathscr A{\kern1.5pt}$
and a hyperplane
$\mathscr A{\kern1.5pt}$
and a hyperplane
 $H_0 \in \pi _1$
such that for the triple
$H_0 \in \pi _1$
such that for the triple
 $({\mathscr A}, {\mathscr A}{\kern1.5pt}', {\mathscr A}{\kern1.5pt}'')$
associated with
$({\mathscr A}, {\mathscr A}{\kern1.5pt}', {\mathscr A}{\kern1.5pt}'')$
associated with
 $H_0$
the restriction map
$H_0$
the restriction map
 ${\varrho } = {\varrho }_{\pi, H_0} :{\kern1pt} {\mathscr A} \setminus \pi _1 \to {\mathscr A}{\kern1.5pt}''$
is bijective and for the induced partitions
${\varrho } = {\varrho }_{\pi, H_0} :{\kern1pt} {\mathscr A} \setminus \pi _1 \to {\mathscr A}{\kern1.5pt}''$
is bijective and for the induced partitions
 $\pi '$
of
$\pi '$
of
 ${\mathscr A}{\kern1.5pt}'$
and
${\mathscr A}{\kern1.5pt}'$
and
 $\pi ''$
of
$\pi ''$
of
 ${\mathscr A}{\kern1.5pt}''$
both
${\mathscr A}{\kern1.5pt}''$
both
 $({\mathscr A}{\kern1.5pt}', \pi ')$
and
$({\mathscr A}{\kern1.5pt}', \pi ')$
and
 $({\mathscr A}{\kern1.5pt}'', \pi '')$
belong to
$({\mathscr A}{\kern1.5pt}'', \pi '')$
belong to
 $\mathcal{IF\!AC}$
, then
$\mathcal{IF\!AC}$
, then
 $({\mathscr A}, \pi )$
also belongs to
$({\mathscr A}, \pi )$
also belongs to
 $\mathcal{IF\!AC}$
.
$\mathcal{IF\!AC}$
.
If
![]() $({\mathscr A}, \pi )$
is in
$({\mathscr A}, \pi )$
is in
![]() $\mathcal{IF\!AC}$
, then we say that
$\mathcal{IF\!AC}$
, then we say that
![]() $\mathscr A{\kern1.5pt}$
is inductively factored with respect to
$\mathscr A{\kern1.5pt}$
is inductively factored with respect to
![]() $\pi$
, or else that
$\pi$
, or else that
![]() $\pi$
is an inductive factorization of
$\pi$
is an inductive factorization of
![]() $\mathscr A$
. Usually, we say
$\mathscr A$
. Usually, we say
![]() $\mathscr A{\kern1.5pt}$
is inductively factored without reference to a specific inductive factorization of
$\mathscr A{\kern1.5pt}$
is inductively factored without reference to a specific inductive factorization of
![]() $\mathscr A$
.
$\mathscr A$
.
Remark 2.18.
-
(i) If
 $\mathscr A{\kern1.5pt}$
is inductively factored, then
$\mathscr A{\kern1.5pt}$
is inductively factored, then
 $\mathscr A{\kern1.5pt}$
is inductively free, by [Reference Hoge and Röhrle24
, Prop. 3.14].
$\mathscr A{\kern1.5pt}$
is inductively free, by [Reference Hoge and Röhrle24
, Prop. 3.14]. -
(ii) Thanks to [Reference Möller and Röhrle31 , Thm. 1.1], inductive factoredness is preserved under localizations.
-
(iii) If
 $\mathscr A{\kern1.5pt}$
is supersolvable, then it is inductively factored, see [Reference Jambu and Paris27] or [Reference Hoge and Röhrle24
, Prop. 3.11].
$\mathscr A{\kern1.5pt}$
is supersolvable, then it is inductively factored, see [Reference Jambu and Paris27] or [Reference Hoge and Röhrle24
, Prop. 3.11].
2.6. Simplicial arrangements
A real arrangement
![]() $\mathscr A{\kern1.5pt}$
is simplicial provided each chamber of the complement of
$\mathscr A{\kern1.5pt}$
is simplicial provided each chamber of the complement of
![]() $\mathscr A{\kern1.5pt}$
is an open simplicial cone in the ambient space. Simpliciality is a combinatorial property. For, thanks to [Reference Cuntz and Geis10, Cor. 2.4], a central essential real
$\mathscr A{\kern1.5pt}$
is an open simplicial cone in the ambient space. Simpliciality is a combinatorial property. For, thanks to [Reference Cuntz and Geis10, Cor. 2.4], a central essential real
![]() $\ell$
-arrangement
$\ell$
-arrangement
![]() $\mathscr A{\kern1.5pt}$
is simplicial if and only if
$\mathscr A{\kern1.5pt}$
is simplicial if and only if
Remark 2.19. Simpliciality is preserved under localizations, see [Reference Cuntz and Mücksch13 , Lem. 2.17(1)].
2.7.
 $K(\pi,1)$
-arrangements
$K(\pi,1)$
-arrangements
A complex
![]() $\ell$
-arrangement
$\ell$
-arrangement
![]() $\mathscr A{\kern1.5pt}$
is called aspherical, or a
$\mathscr A{\kern1.5pt}$
is called aspherical, or a
![]() $K(\pi,1)$
-arrangement (or that
$K(\pi,1)$
-arrangement (or that
![]() $\mathscr A{\kern1.5pt}$
is
$\mathscr A{\kern1.5pt}$
is
![]() $K(\pi,1)$
for short), provided the complement
$K(\pi,1)$
for short), provided the complement
![]() $M({\mathscr A}{\kern1.5pt})$
of the union of the hyperplanes in
$M({\mathscr A}{\kern1.5pt})$
of the union of the hyperplanes in
![]() $\mathscr A{\kern1.5pt}$
in
$\mathscr A{\kern1.5pt}$
in
![]() ${\mathbb C}^\ell$
is aspherical, that is, is a
${\mathbb C}^\ell$
is aspherical, that is, is a
![]() $K(\pi,1)$
-space. That is, the universal covering space of
$K(\pi,1)$
-space. That is, the universal covering space of
![]() $M({\mathscr A}{\kern1.5pt})$
is contractible and the fundamental group
$M({\mathscr A}{\kern1.5pt})$
is contractible and the fundamental group
![]() $\pi _1(M({\mathscr A}{\kern1.5pt}))$
of
$\pi _1(M({\mathscr A}{\kern1.5pt}))$
of
![]() $M({\mathscr A}{\kern1.5pt})$
is isomorphic to the group
$M({\mathscr A}{\kern1.5pt})$
is isomorphic to the group
![]() $\pi$
. This is an important topological property, for the cohomology ring
$\pi$
. This is an important topological property, for the cohomology ring
![]() $H^*(X, {\mathbb Z})$
of a
$H^*(X, {\mathbb Z})$
of a
![]() $K(\pi,1)$
-space
$K(\pi,1)$
-space
![]() $X$
coincides with the group cohomology
$X$
coincides with the group cohomology
![]() $H^*(\pi, {\mathbb Z})$
of
$H^*(\pi, {\mathbb Z})$
of
![]() $\pi$
. The crucial point here is that the intersections of codimension
$\pi$
. The crucial point here is that the intersections of codimension
![]() $2$
determine the fundamental group
$2$
determine the fundamental group
![]() $\pi _1(M({\mathscr A}{\kern1.5pt}))$
of
$\pi _1(M({\mathscr A}{\kern1.5pt}))$
of
![]() $M({\mathscr A}{\kern1.5pt})$
.
$M({\mathscr A}{\kern1.5pt})$
.
Remark 2.20.
-
(i) By Deligne’s seminal work [Reference Deligne14], complexified simplicial arrangements are
 $K(\pi, 1)$
. Likewise for complex supersolvable arrangements, cf. [Reference Falk and Randell20] and [Reference Terao45] (cf. [Reference Orlik and Terao34
, Prop. 5.12, Thm. 5.113]).
$K(\pi, 1)$
. Likewise for complex supersolvable arrangements, cf. [Reference Falk and Randell20] and [Reference Terao45] (cf. [Reference Orlik and Terao34
, Prop. 5.12, Thm. 5.113]). -
(ii) Thanks to an observation by Oka, asphericity is preserved under localizations, for example see [Reference Paris35 , Lem. 1.1].
-
(iii) By work of Hattori, generic arrangements are not
 $K(\pi, 1)$
, [Reference Orlik and Terao34
, Cor. 5.23].
$K(\pi, 1)$
, [Reference Orlik and Terao34
, Cor. 5.23].
3. Proof of Theorem 1.2
We begin by identifying the small rank hyperpolygonal arrangements
![]() ${\mathscr H}_n$
with known ones. Clearly,
${\mathscr H}_n$
with known ones. Clearly,
![]() ${\mathscr H}_2$
is just the reflection arrangement of the Weyl group of type
${\mathscr H}_2$
is just the reflection arrangement of the Weyl group of type
![]() $B_2$
.
$B_2$
.
It follows from the next lemma that
![]() ${\mathscr H}_3$
is linearly isomorphic to the connected subgraph arrangement
${\mathscr H}_3$
is linearly isomorphic to the connected subgraph arrangement
![]() ${\mathscr A}_G$
, where
${\mathscr A}_G$
, where
![]() $G = C_3$
is the cycle graph on three vertices. See [Reference Cuntz and Kühne12] for the class of connected subgraph arrangements.
$G = C_3$
is the cycle graph on three vertices. See [Reference Cuntz and Kühne12] for the class of connected subgraph arrangements.
Lemma 3.1. The arrangements
![]() ${\mathscr H}_3$
and
${\mathscr H}_3$
and
![]() ${\mathscr A}_{C_3}$
are linearly isomorphic.
${\mathscr A}_{C_3}$
are linearly isomorphic.
Proof. One checks that (up to scalar multiples) the map on linear forms
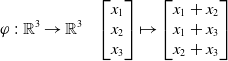 \begin{equation*}\varphi\ :\ {\mathbb R}^3 \rightarrow {\mathbb R}^3 \ \ \ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \mapsto \begin{bmatrix} x_1+x_2 \\ x_1+x_3 \\ x_2+x_3 \end{bmatrix}\end{equation*}
\begin{equation*}\varphi\ :\ {\mathbb R}^3 \rightarrow {\mathbb R}^3 \ \ \ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \mapsto \begin{bmatrix} x_1+x_2 \\ x_1+x_3 \\ x_2+x_3 \end{bmatrix}\end{equation*}
gives a linear isomorphism between
![]() ${\mathscr H}_3$
and
${\mathscr H}_3$
and
![]() ${\mathscr A}_{C_3}$
.
${\mathscr A}_{C_3}$
.
We also note that
![]() ${\mathscr H}_3$
is linearly isomorphic to the cone over the Shi arrangement of type
${\mathscr H}_3$
is linearly isomorphic to the cone over the Shi arrangement of type
![]() $A_2$
, by means of Lemma 3.1 and [Reference Cuntz and Kühne12, Prop. 3.1].
$A_2$
, by means of Lemma 3.1 and [Reference Cuntz and Kühne12, Prop. 3.1].
Our next lemma shows that
![]() ${\mathscr H}_4$
is linearly isomorphic to the reflection arrangement
${\mathscr H}_4$
is linearly isomorphic to the reflection arrangement
![]() ${\mathscr A}(D_4)$
of the Weyl group of type
${\mathscr A}(D_4)$
of the Weyl group of type
![]() $D_4$
.
$D_4$
.
Lemma 3.2. The arrangements
![]() ${\mathscr H}_4$
and
${\mathscr H}_4$
and
![]() ${\mathscr A}(D_4)$
are linearly isomorphic.
${\mathscr A}(D_4)$
are linearly isomorphic.
Proof. One checks that (up to scalar multiples) the map on linear forms
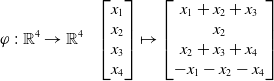 \begin{equation*}\varphi\ :\ {\mathbb R}^4 \rightarrow {\mathbb R}^4 \ \ \ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} \mapsto \begin{bmatrix} x_1+x_2+x_3 \\ x_2 \\ x_2+x_3+x_4 \\ -x_1-x_2-x_4 \end{bmatrix}\end{equation*}
\begin{equation*}\varphi\ :\ {\mathbb R}^4 \rightarrow {\mathbb R}^4 \ \ \ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} \mapsto \begin{bmatrix} x_1+x_2+x_3 \\ x_2 \\ x_2+x_3+x_4 \\ -x_1-x_2-x_4 \end{bmatrix}\end{equation*}
gives a linear isomorphism between
![]() ${\mathscr H}_4$
and
${\mathscr H}_4$
and
![]() ${\mathscr A}(D_4)$
.
${\mathscr A}(D_4)$
.
Our next lemma gives that the reverse implications in the statements in Theorem 1.2 hold for
![]() $n\ge 6$
.
$n\ge 6$
.
Lemma 3.3. Let
![]() $n \ge 6$
. Then there exists a generic rank
$n \ge 6$
. Then there exists a generic rank
![]() $3$
localization of
$3$
localization of
![]() ${\mathscr H}_n$
. As a consequence, for
${\mathscr H}_n$
. As a consequence, for
![]() $n \ge 6$
,
$n \ge 6$
,
![]() ${\mathscr H}_n$
is not free (and so is not supersolvable, not inductively free, and not inductively factored), it is also not
${\mathscr H}_n$
is not free (and so is not supersolvable, not inductively free, and not inductively factored), it is also not
![]() $K(\pi,1)$
(and so is also not simplicial).
$K(\pi,1)$
(and so is also not simplicial).
Proof. For
![]() $n = 6$
, let
$n = 6$
, let
![]() $I_1 :\!= \{1\}, I_2 :\!= \{1, 2,3\}, I_3 :\!= \{1, 4,5\}$
,
$I_1 :\!= \{1\}, I_2 :\!= \{1, 2,3\}, I_3 :\!= \{1, 4,5\}$
,
![]() $I_4 :\!= \{1, 2,3, 4,5\}$
, and define
$I_4 :\!= \{1, 2,3, 4,5\}$
, and define
![]() $X = \cap _{i = 1}^4 H_{I_i} \in L({\mathscr H}_6)$
. Then, as the localization
$X = \cap _{i = 1}^4 H_{I_i} \in L({\mathscr H}_6)$
. Then, as the localization
![]() $({\mathscr H}_6)_X$
consists of precisely the four hyperplanes
$({\mathscr H}_6)_X$
consists of precisely the four hyperplanes
![]() $H_{I_1}, \ldots, H_{I_4}$
of
$H_{I_1}, \ldots, H_{I_4}$
of
![]() ${\mathscr H}_6$
, we infer that
${\mathscr H}_6$
, we infer that
![]() $({\mathscr H}_6)_X$
is generic of rank
$({\mathscr H}_6)_X$
is generic of rank
![]() $3$
, see [Reference Rose and Terao39, Ex. 4.5.6].
$3$
, see [Reference Rose and Terao39, Ex. 4.5.6].
Generalizing this example for
![]() $n \gt 6$
, for
$n \gt 6$
, for
![]() $X = \cap _{i = 1}^4 H_{I_i} \in L({\mathscr H}_n)$
, the very same argument shows that also the localization
$X = \cap _{i = 1}^4 H_{I_i} \in L({\mathscr H}_n)$
, the very same argument shows that also the localization
![]() $({\mathscr H}_n)_X$
in
$({\mathscr H}_n)_X$
in
![]() ${\mathscr H}_n$
is still generic of rank
${\mathscr H}_n$
is still generic of rank
![]() $3$
.
$3$
.
It follows from Remark 2.4(i) that
![]() $({\mathscr H}_n)_X$
is not free and from Remark 2.20(iii) that
$({\mathscr H}_n)_X$
is not free and from Remark 2.20(iii) that
![]() $({\mathscr H}_n)_X$
is not
$({\mathscr H}_n)_X$
is not
![]() $K(\pi,1)$
. Consequently,
$K(\pi,1)$
. Consequently,
![]() $({\mathscr H}_n)_X$
is not supersolvable, not inductively free, not inductively factored, and not simplicial. And as all of the latter are local properties, thanks to Remarks 2.3(ii), 2.4(ii), 2.8(ii), 2.18(ii), 2.19, and 2.20(ii), the lemma follows.
$({\mathscr H}_n)_X$
is not supersolvable, not inductively free, not inductively factored, and not simplicial. And as all of the latter are local properties, thanks to Remarks 2.3(ii), 2.4(ii), 2.8(ii), 2.18(ii), 2.19, and 2.20(ii), the lemma follows.
Thus, it remains to show the forward implications in the statements in Theorem 1.2 and the remaining reverse implications for
![]() $n \le 5$
.
$n \le 5$
.
Part (i). Thanks to Remark 2.3 (i),
![]() ${\mathscr H}_2$
is supersolvable. It follows from Lemma 3.1 and [Reference Cuntz and Kühne12, Cor. 8.11] that
${\mathscr H}_2$
is supersolvable. It follows from Lemma 3.1 and [Reference Cuntz and Kühne12, Cor. 8.11] that
![]() ${\mathscr H}_3$
is not supersolvable. By [Reference Hoge and Röhrle25, Lem. 3.2],
${\mathscr H}_3$
is not supersolvable. By [Reference Hoge and Röhrle25, Lem. 3.2],
![]() ${\mathscr A}(D_4)$
is not factored (thus not inductively factored), thus, thanks to Lemma 3.2, neither is
${\mathscr A}(D_4)$
is not factored (thus not inductively factored), thus, thanks to Lemma 3.2, neither is
![]() ${\mathscr H}_4$
, so the latter is not supersolvable, by Remark 2.18 (iii). Thanks to [Reference Edelman and Reiner17],
${\mathscr H}_4$
, so the latter is not supersolvable, by Remark 2.18 (iii). Thanks to [Reference Edelman and Reiner17],
![]() ${\mathscr H}_5$
is not inductively free, thus by Remark 2.8 (iii) it is not supersolvable. Thus Theorem 1.2 (i) now follows from Lemma 3.3.
${\mathscr H}_5$
is not inductively free, thus by Remark 2.8 (iii) it is not supersolvable. Thus Theorem 1.2 (i) now follows from Lemma 3.3.
Part (ii). It follows from [Reference Giordani, Möller, Mücksch and Röhrle23, Thm. 1.7] that
![]() ${\mathscr A}_{C_3}$
is inductively factored, thus so is
${\mathscr A}_{C_3}$
is inductively factored, thus so is
![]() ${\mathscr H}_3$
, by Lemma 3.1. We have already observed above that
${\mathscr H}_3$
, by Lemma 3.1. We have already observed above that
![]() ${\mathscr H}_4$
is not inductively factored. Since
${\mathscr H}_4$
is not inductively factored. Since
![]() ${\mathscr H}_5$
is not inductively free, it is also not inductively factored, by Remark 2.18 (i). Consequently, Theorem 1.2 (ii) follows again from Lemma 3.3.
${\mathscr H}_5$
is not inductively free, it is also not inductively factored, by Remark 2.18 (i). Consequently, Theorem 1.2 (ii) follows again from Lemma 3.3.
Part (iii). For
![]() $n \le 4$
, the arrangements
$n \le 4$
, the arrangements
![]() ${\mathscr H}_n$
are inductively free: For
${\mathscr H}_n$
are inductively free: For
![]() $n \le 3$
, this follows from Theorem 1.2 (ii) and Remark 2.18 (i). For
$n \le 3$
, this follows from Theorem 1.2 (ii) and Remark 2.18 (i). For
![]() ${\mathscr H}_4$
this follows from Lemma 3.2 and [Reference Jambu and Terao28, Ex. 2.6]. Edelman and Reiner [Reference Edelman and Reiner17] have observed that
${\mathscr H}_4$
this follows from Lemma 3.2 and [Reference Jambu and Terao28, Ex. 2.6]. Edelman and Reiner [Reference Edelman and Reiner17] have observed that
![]() ${\mathscr H}_5$
is free but not inductively free. Consequently, Theorem 1.2 (iii) follows from Lemma 3.3.
${\mathscr H}_5$
is free but not inductively free. Consequently, Theorem 1.2 (iii) follows from Lemma 3.3.
Part (iv). By Theorem 1.2 (iii) and [Reference Edelman and Reiner17],
![]() ${\mathscr H}_n$
is free for
${\mathscr H}_n$
is free for
![]() $n \le 5$
. Whence Theorem 1.2 (iv) is once again a consequence of Lemma 3.3.
$n \le 5$
. Whence Theorem 1.2 (iv) is once again a consequence of Lemma 3.3.
Part (v). With the aid of the formula (2.1), it is straightforward to check that
![]() ${\mathscr H}_n$
is simplicial for
${\mathscr H}_n$
is simplicial for
![]() $n \le 4$
and that
$n \le 4$
and that
![]() ${\mathscr H}_5$
is no longer simplicial. So Theorem 1.2 (v) follows from Lemma 3.3.
${\mathscr H}_5$
is no longer simplicial. So Theorem 1.2 (v) follows from Lemma 3.3.
Finally, Theorem 1.2 (vi) is immediate from Lemma 3.3.
In closing this section, we show that
![]() ${\mathscr H}_5$
is still recursively free, a concept originally due to Ziegler [Reference Ziegler48]; see [Reference Orlik and Terao34, Def. 4.60].
${\mathscr H}_5$
is still recursively free, a concept originally due to Ziegler [Reference Ziegler48]; see [Reference Orlik and Terao34, Def. 4.60].
Remark 3.4. While
![]() ${\mathscr H}_5$
is not inductively free, one can show that it is still recursively free. We sketch the argument. First one checks that
${\mathscr H}_5$
is not inductively free, one can show that it is still recursively free. We sketch the argument. First one checks that
![]() ${\mathscr A} = {\mathscr H}_5 \cup \{\ker (x_2 - x_4)\}$
is inductively free with
${\mathscr A} = {\mathscr H}_5 \cup \{\ker (x_2 - x_4)\}$
is inductively free with
![]() $\exp ({\mathscr A}{\kern1.5pt}) = \{1,5,5,5,6\}$
. Next one checks that
$\exp ({\mathscr A}{\kern1.5pt}) = \{1,5,5,5,6\}$
. Next one checks that
![]() ${\mathscr B}{\kern2pt} :\!= {\mathscr A}^{{\kern1.5pt}\ker (x_2 - x_4)}$
is itself again recursively free with
${\mathscr B}{\kern2pt} :\!= {\mathscr A}^{{\kern1.5pt}\ker (x_2 - x_4)}$
is itself again recursively free with
![]() $\exp ({\mathscr B}) = \{1,5,5,5\}$
. Owing to [Reference Orlik and Terao34
, Def. 4.60],
$\exp ({\mathscr B}) = \{1,5,5,5\}$
. Owing to [Reference Orlik and Terao34
, Def. 4.60],
![]() ${\mathscr H}_5$
is recursively free. To see in turn that
${\mathscr H}_5$
is recursively free. To see in turn that
![]() $\mathscr B$
is recursively free, one first checks that
$\mathscr B$
is recursively free, one first checks that
![]() ${\mathscr C}{\kern2pt} :\!= {\mathscr B} \cup \{\ker (x_1 - x_3)\}$
is inductively free with
${\mathscr C}{\kern2pt} :\!= {\mathscr B} \cup \{\ker (x_1 - x_3)\}$
is inductively free with
![]() $\exp ({\mathscr C}) = \{1,5,5,6\}$
. Then one checks that
$\exp ({\mathscr C}) = \{1,5,5,6\}$
. Then one checks that
![]() ${\mathscr D}{\kern2pt} :\!= {\mathscr C}^{{\kern1.5pt}\ker (x_1 - x_3)}$
is free with
${\mathscr D}{\kern2pt} :\!= {\mathscr C}^{{\kern1.5pt}\ker (x_1 - x_3)}$
is free with
![]() $\exp {\mathscr D} = \{1,5,5\}$
. Thanks to [Reference Abe, Cuntz, Kawanoue and Nozawa2
, Thm. 1.1],
$\exp {\mathscr D} = \{1,5,5\}$
. Thanks to [Reference Abe, Cuntz, Kawanoue and Nozawa2
, Thm. 1.1],
![]() $\mathscr D$
is recursively free. Thus, again by [Reference Orlik and Terao34
, Def. 4.60],
$\mathscr D$
is recursively free. Thus, again by [Reference Orlik and Terao34
, Def. 4.60],
![]() $\mathscr B$
is recursively free.
$\mathscr B$
is recursively free.
It thus follows from the paragraph above about
![]() ${\mathscr H}_5$
and Theorem 1.2 (iv) that
${\mathscr H}_5$
and Theorem 1.2 (iv) that
![]() ${\mathscr H}_n$
is free if and only if
${\mathscr H}_n$
is free if and only if
![]() ${\mathscr H}_n$
is recursively free. In general, these two notions differ, see [Reference Cuntz and Hoge11].
${\mathscr H}_n$
is recursively free. In general, these two notions differ, see [Reference Cuntz and Hoge11].
4. Projective uniqueness: proof of Theorem 1.5
Definition 4.1. Let
![]() $\mathscr A$
,
$\mathscr A$
,
![]() $\mathscr B$
be two arrangements in a finite-dimensional
$\mathscr B$
be two arrangements in a finite-dimensional
![]() $\mathbb R$
-vector space
$\mathbb R$
-vector space
![]() $V$
.
$V$
.
-
(i)
 $\mathscr A{\kern1.5pt}$
and
$\mathscr A{\kern1.5pt}$
and
 $\mathscr B$
are linearly isomorphic if there is a
$\mathscr B$
are linearly isomorphic if there is a
 $\varphi \in \operatorname {GL}(V)$
such that
$\varphi \in \operatorname {GL}(V)$
such that
 ${\mathscr B} = \{\varphi (H) \mid H \in {\mathscr A}\}$
; denoted by
${\mathscr B} = \{\varphi (H) \mid H \in {\mathscr A}\}$
; denoted by
 ${\mathscr A} \cong {\mathscr B}$
.
${\mathscr A} \cong {\mathscr B}$
. -
(ii)
 $\mathscr A{\kern1.5pt}$
and
$\mathscr A{\kern1.5pt}$
and
 $\mathscr B$
are
$\mathscr B$
are
 ${L}$
-equivalent if
${L}$
-equivalent if
 $L({\mathscr A}{\kern1.5pt})$
and
$L({\mathscr A}{\kern1.5pt})$
and
 $L({\mathscr B})$
are isomorphic as posets; denoted by
$L({\mathscr B})$
are isomorphic as posets; denoted by
 ${\mathscr A} \cong _L {\mathscr B}$
.
${\mathscr A} \cong _L {\mathscr B}$
. -
(iii)
 $\mathscr A{\kern1.5pt}$
is projectively unique if for any arrangement
$\mathscr A{\kern1.5pt}$
is projectively unique if for any arrangement
 $\mathscr C$
in
$\mathscr C$
in
 $V$
we have:
$V$
we have:
 ${\mathscr C} \cong _L {\mathscr A}$
implies
${\mathscr C} \cong _L {\mathscr A}$
implies
 ${\mathscr C} \cong {\mathscr A}$
.
${\mathscr C} \cong {\mathscr A}$
.
We recall some results from [Reference Giordani, Möller, Mücksch and Röhrle23]. Let
![]() $\mathscr A{\kern1.5pt}$
be an
$\mathscr A{\kern1.5pt}$
be an
![]() $\mathbb R$
-arrangement. We specify what we mean by a subarrangement of
$\mathbb R$
-arrangement. We specify what we mean by a subarrangement of
![]() $\mathscr A{\kern1.5pt}$
being generated by a subarrangement of
$\mathscr A{\kern1.5pt}$
being generated by a subarrangement of
![]() $\mathscr A$
.
$\mathscr A$
.
Definition 4.2. Let
![]() $\varnothing \ne S \subseteq {\mathscr A}$
. Set
$\varnothing \ne S \subseteq {\mathscr A}$
. Set
![]() $\operatorname {Gen}_0({\mathscr A},S){\kern2pt} :\!= S$
and inductively
$\operatorname {Gen}_0({\mathscr A},S){\kern2pt} :\!= S$
and inductively
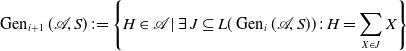 \begin{equation*}\operatorname {Gen}_{i+1}({\mathscr A},S){\kern2pt} :\!= \left \{H \in {\mathscr A} \mid \exists \ J \subseteq L(\operatorname {Gen}_i({\mathscr A},S)) \,:\, H = \sum _{X \in J} X \right \}\end{equation*}
\begin{equation*}\operatorname {Gen}_{i+1}({\mathscr A},S){\kern2pt} :\!= \left \{H \in {\mathscr A} \mid \exists \ J \subseteq L(\operatorname {Gen}_i({\mathscr A},S)) \,:\, H = \sum _{X \in J} X \right \}\end{equation*}
for
![]() $i \ge 0$
. Then we say that
$i \ge 0$
. Then we say that
is the subarrangement of
![]() $\mathscr A{\kern1.5pt}$
generated by
$\mathscr A{\kern1.5pt}$
generated by
![]() $S$
. If
$S$
. If
![]() $\langle S \rangle _{\mathscr A} = {\mathscr A}$
, then we say that
$\langle S \rangle _{\mathscr A} = {\mathscr A}$
, then we say that
![]() $S$
generates
$S$
generates
![]() $\mathscr A$
.
$\mathscr A$
.
Lemma 4.3 [Reference Giordani, Möller, Mücksch and Röhrle23, Lem. 3.5]. Let
![]() $\mathscr A{\kern1.5pt}$
and
$\mathscr A{\kern1.5pt}$
and
![]() $\mathscr B$
be two arrangements in
$\mathscr B$
be two arrangements in
![]() $V$
. Suppose
$V$
. Suppose
![]() $\varnothing \ne S \subseteq {\mathscr A}$
,
$\varnothing \ne S \subseteq {\mathscr A}$
,
![]() $\varnothing \ne T \subseteq {\mathscr B}$
such that
$\varnothing \ne T \subseteq {\mathscr B}$
such that
![]() $\langle S \rangle _{\mathscr A} = {\mathscr A}$
and
$\langle S \rangle _{\mathscr A} = {\mathscr A}$
and
![]() $\langle T \rangle _{\mathscr B} = {\mathscr B}$
, that is
$\langle T \rangle _{\mathscr B} = {\mathscr B}$
, that is
![]() $S$
generates
$S$
generates
![]() $\mathscr A{\kern1.5pt}$
and
$\mathscr A{\kern1.5pt}$
and
![]() $T$
generates
$T$
generates
![]() $\mathscr B$
. If
$\mathscr B$
. If
![]() $\mathscr A{\kern1.5pt}$
and
$\mathscr A{\kern1.5pt}$
and
![]() $\mathscr B$
are
$\mathscr B$
are
![]() $L$
-equivalent via a poset isomorphism
$L$
-equivalent via a poset isomorphism
![]() $\psi :L({\mathscr A}{\kern1.5pt})\to L({\mathscr B})$
and
$\psi :L({\mathscr A}{\kern1.5pt})\to L({\mathscr B})$
and
![]() $\varphi \in \operatorname {GL}(V)$
such that
$\varphi \in \operatorname {GL}(V)$
such that
![]() $\psi (S) = \varphi (S) = T$
and
$\psi (S) = \varphi (S) = T$
and
![]() $\psi (H) = \varphi (H)$
for all
$\psi (H) = \varphi (H)$
for all
![]() $H \in S$
, then
$H \in S$
, then
![]() $\varphi$
extends to a linear isomorphism between the whole arrangements, that is
$\varphi$
extends to a linear isomorphism between the whole arrangements, that is
![]() $\varphi ({\mathscr A}{\kern1.5pt}) = {\mathscr B}$
.
$\varphi ({\mathscr A}{\kern1.5pt}) = {\mathscr B}$
.
The following is a consequence of Lemma 4.3.
Proposition 4.4 [Reference Giordani, Möller, Mücksch and Röhrle23, Prop. 3.6]. Let
![]() $\mathscr A{\kern1.5pt}$
be an essential and irreducible arrangement in
$\mathscr A{\kern1.5pt}$
be an essential and irreducible arrangement in
![]() $V \cong {\mathbb R}^\ell$
. Suppose there is a subset
$V \cong {\mathbb R}^\ell$
. Suppose there is a subset
![]() $S$
of
$S$
of
![]() $\mathscr A{\kern1.5pt}$
such that
$\mathscr A{\kern1.5pt}$
such that
![]() $\langle S \rangle _{\mathscr A} = {\mathscr A}$
and
$\langle S \rangle _{\mathscr A} = {\mathscr A}$
and
![]() $|S| = \ell +1$
. Then
$|S| = \ell +1$
. Then
![]() $\mathscr A{\kern1.5pt}$
is projectively unique.
$\mathscr A{\kern1.5pt}$
is projectively unique.
Finally, the following result gives Theorem 1.5.
Proposition 4.5. Let
![]() $ n \ge 1$
and let
$ n \ge 1$
and let
Then
![]() $\langle S \rangle _{{\mathscr H}_n} = {\mathscr H}_n$
. In particular,
$\langle S \rangle _{{\mathscr H}_n} = {\mathscr H}_n$
. In particular,
![]() ${\mathscr H}_n$
is projectively unique over
${\mathscr H}_n$
is projectively unique over
![]() $\mathbb R$
.
$\mathbb R$
.
Proof. Let
![]() $\varnothing \ne I \subseteq [n]$
. Without loss, we may assume that
$\varnothing \ne I \subseteq [n]$
. Without loss, we may assume that
![]() $n \notin I$
. For
$n \notin I$
. For
![]() $i \in [n-1]$
, set
$i \in [n-1]$
, set
![]() $H_i :\!= \ker x_i$
, and for
$H_i :\!= \ker x_i$
, and for
![]() $\alpha :\!= x_1 + \ldots + x_n$
and
$\alpha :\!= x_1 + \ldots + x_n$
and
![]() $\beta :\!= x_1 + \ldots + x_{n-1} - x_n$
, set
$\beta :\!= x_1 + \ldots + x_{n-1} - x_n$
, set
![]() $H_\alpha :\!= \ker \alpha$
and
$H_\alpha :\!= \ker \alpha$
and
![]() $H_\beta :\!= \ker \beta$
. Then
$H_\beta :\!= \ker \beta$
. Then
![]() $H_I = \ker \left (\sum _{i \in I}x_i - \sum _{j \in [n]\setminus I}x_j\right ) = \ker \gamma$
, where
$H_I = \ker \left (\sum _{i \in I}x_i - \sum _{j \in [n]\setminus I}x_j\right ) = \ker \gamma$
, where
It follows from (4.6) that
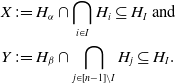 \begin{align*} X & {\kern2pt}:\!= H_\alpha \cap \bigcap _{i \in I} H_i \subseteq H_I \text{ and } \\ Y &{\kern2pt} :\!= H_\beta \cap \bigcap _{j \in [n-1]\setminus I} H_j \subseteq H_I. \end{align*}
\begin{align*} X & {\kern2pt}:\!= H_\alpha \cap \bigcap _{i \in I} H_i \subseteq H_I \text{ and } \\ Y &{\kern2pt} :\!= H_\beta \cap \bigcap _{j \in [n-1]\setminus I} H_j \subseteq H_I. \end{align*}
Since
![]() $\dim X = n - |I| - 1$
,
$\dim X = n - |I| - 1$
,
![]() $\dim Y = |I|$
, and
$\dim Y = |I|$
, and
![]() $\dim (X \cap Y) = 0$
, we have
$\dim (X \cap Y) = 0$
, we have
![]() $H_I = X + Y$
. Since both
$H_I = X + Y$
. Since both
![]() $X$
and
$X$
and
![]() $Y$
belong to the lattice of intersections of the subarrangement
$Y$
belong to the lattice of intersections of the subarrangement
![]() $S$
of
$S$
of
![]() ${\mathscr H}_n$
, we infer
${\mathscr H}_n$
, we infer
![]() $H_I = X + Y \in \langle S \rangle _{{\mathscr H}_n}$
. Consequently, the result follows thanks to Proposition 4.4.
$H_I = X + Y \in \langle S \rangle _{{\mathscr H}_n}$
. Consequently, the result follows thanks to Proposition 4.4.
5. Combinatorial Formality: proof of Theorem 1.6
A property for arrangements is said to be combinatorial if it only depends on the intersection lattice of the underlying arrangement. Yuzvinsky [Reference Yuzvinsky47, Ex. 2.2] demonstrated that formality is not combinatorial, answering a question raised by Falk and Randell [Reference Falk and Randell21] in the negative. Yuzvinsky’s insight motivates the following notion from [Reference Möller, Mücksch and Röhrle30].
Definition 5.1. Suppose
![]() $\mathscr A{\kern1.5pt}$
is a formal arrangement. We say
$\mathscr A{\kern1.5pt}$
is a formal arrangement. We say
![]() $\mathscr A{\kern1.5pt}$
is combinatorially formal if every arrangement with an intersection lattice isomorphic to the one of
$\mathscr A{\kern1.5pt}$
is combinatorially formal if every arrangement with an intersection lattice isomorphic to the one of
![]() $\mathscr A{\kern1.5pt}$
is also formal.
$\mathscr A{\kern1.5pt}$
is also formal.
The following definitions, which are originally due to Falk for matroids [Reference Falk19], were adapted for arrangements in [Reference Möller, Mücksch and Röhrle30, §2.4]. Let
![]() ${\mathscr B} \subset {\mathscr A}$
be a subset of hyperplanes. We say
${\mathscr B} \subset {\mathscr A}$
be a subset of hyperplanes. We say
![]() $\mathscr B$
is closed if
$\mathscr B$
is closed if
![]() ${\mathscr B} ={\mathscr A}_Y$
for
${\mathscr B} ={\mathscr A}_Y$
for
![]() $Y=\bigcap \limits _{H\in {\mathscr B}} H$
. We call
$Y=\bigcap \limits _{H\in {\mathscr B}} H$
. We call
![]() ${\mathscr B}$
line-closed if for every pair
${\mathscr B}$
line-closed if for every pair
![]() $H,H'\in {\mathscr B}$
of hyperplanes, we have
$H,H'\in {\mathscr B}$
of hyperplanes, we have
![]() ${\mathscr A}_{H\cap H'}\subset {\mathscr B}$
. The line-closure
${\mathscr A}_{H\cap H'}\subset {\mathscr B}$
. The line-closure
![]() ${\operatorname {lc}}({\mathscr B})$
of
${\operatorname {lc}}({\mathscr B})$
of
![]() ${\mathscr B}$
is defined as the intersection of all line-closed subsets of
${\mathscr B}$
is defined as the intersection of all line-closed subsets of
![]() $\mathscr A{\kern1.5pt}$
containing
$\mathscr A{\kern1.5pt}$
containing
![]() $\mathscr B$
. The arrangement
$\mathscr B$
. The arrangement
![]() $\mathscr A{\kern1.5pt}$
is called line-closed if every line-closed subset of
$\mathscr A{\kern1.5pt}$
is called line-closed if every line-closed subset of
![]() $\mathscr A{\kern1.5pt}$
is closed. With these notions, we have the following criterion for combinatorial formality, see [Reference Falk19, Cor. 3.8], [Reference Möller, Mücksch and Röhrle30, Prop. 3.2]:
$\mathscr A{\kern1.5pt}$
is closed. With these notions, we have the following criterion for combinatorial formality, see [Reference Falk19, Cor. 3.8], [Reference Möller, Mücksch and Röhrle30, Prop. 3.2]:
Proposition 5.2. Let
![]() $\mathscr A{\kern1.5pt}$
be an arrangement of rank
$\mathscr A{\kern1.5pt}$
be an arrangement of rank
![]() $r$
. Suppose
$r$
. Suppose
![]() ${\mathscr B} \subseteq {\mathscr A}$
consists of
${\mathscr B} \subseteq {\mathscr A}$
consists of
![]() $r$
hyperplanes such that
$r$
hyperplanes such that
![]() $r({\mathscr B})=r$
and
$r({\mathscr B})=r$
and
![]() ${\operatorname {lc}}({\mathscr B})={\mathscr A}$
. Then
${\operatorname {lc}}({\mathscr B})={\mathscr A}$
. Then
![]() $\mathscr A{\kern1.5pt}$
is combinatorially formal.
$\mathscr A{\kern1.5pt}$
is combinatorially formal.
A subset
![]() ${\mathscr B} \subseteq {\mathscr A}$
as in Proposition 5.2 is called an lc-basis of
${\mathscr B} \subseteq {\mathscr A}$
as in Proposition 5.2 is called an lc-basis of
![]() $\mathscr A$
.
$\mathscr A$
.
Proof of Theorem 1.6. Let
![]() ${\mathscr B} = \{\ker x_1, \ldots, \ker x_{n-1}, \ker (x_1 + \ldots + x_n)\} \subseteq {\mathscr H}_n$
. Then it is easy to see that successively all
${\mathscr B} = \{\ker x_1, \ldots, \ker x_{n-1}, \ker (x_1 + \ldots + x_n)\} \subseteq {\mathscr H}_n$
. Then it is easy to see that successively all
![]() $H_I$
for
$H_I$
for
![]() $\varnothing \ne I \subseteq [n]$
belong to the line-closure
$\varnothing \ne I \subseteq [n]$
belong to the line-closure
![]() ${\operatorname {lc}}({\mathscr B})$
of
${\operatorname {lc}}({\mathscr B})$
of
![]() $\mathscr B$
, as follows. For
$\mathscr B$
, as follows. For
![]() $i \in [n]$
, set
$i \in [n]$
, set
![]() $H_i :\!= \ker x_i$
, and for
$H_i :\!= \ker x_i$
, and for
![]() $\alpha :\!= x_1 + \ldots + x_n$
set
$\alpha :\!= x_1 + \ldots + x_n$
set
![]() $H_\alpha :\!= \ker \alpha$
. Then for
$H_\alpha :\!= \ker \alpha$
. Then for
![]() $I = [n]\setminus \{i\}$
, we have
$I = [n]\setminus \{i\}$
, we have
![]() $H_I = \ker \left (\alpha -2 x_i\right ) \supset H_\alpha \cap H_i$
. Thus for each
$H_I = \ker \left (\alpha -2 x_i\right ) \supset H_\alpha \cap H_i$
. Thus for each
![]() $I$
of cardinality
$I$
of cardinality
![]() $n-1$
,
$n-1$
,
![]() $H_I$
belongs to
$H_I$
belongs to
![]() ${\operatorname {lc}}({\mathscr B})$
. Now iterate the argument above for
${\operatorname {lc}}({\mathscr B})$
. Now iterate the argument above for
![]() $I$
of successively smaller cardinality. Consequently,
$I$
of successively smaller cardinality. Consequently,
![]() ${\operatorname {lc}}({\mathscr B}) = {\mathscr H}_n$
. Since
${\operatorname {lc}}({\mathscr B}) = {\mathscr H}_n$
. Since
![]() $\operatorname {rk}({\mathscr H}_n) = n = |{\mathscr B}| = \operatorname {rk}({\mathscr B})$
, it follows from Proposition 5.2 that
$\operatorname {rk}({\mathscr H}_n) = n = |{\mathscr B}| = \operatorname {rk}({\mathscr B})$
, it follows from Proposition 5.2 that
![]() ${\mathscr H}_n$
is combinatorially formal.
${\mathscr H}_n$
is combinatorially formal.
There is a stronger notion of formality for an arrangement
![]() $\mathscr A$
, that of
$\mathscr A$
, that of
![]() $k$
-formality for
$k$
-formality for
![]() $1 \le k \le \operatorname {rk}({\mathscr A}{\kern1.5pt})$
due to Brandt and Terao [Reference Brandt and Terao9]. In view of Theorem 1.6 and in view of the fact that all free arrangements are not just formal but are
$1 \le k \le \operatorname {rk}({\mathscr A}{\kern1.5pt})$
due to Brandt and Terao [Reference Brandt and Terao9]. In view of Theorem 1.6 and in view of the fact that all free arrangements are not just formal but are
![]() $k$
-formal for all
$k$
-formal for all
![]() $k$
, by [Reference Brandt and Terao9, Thm. 4.15], one might ask for this stronger notion of
$k$
, by [Reference Brandt and Terao9, Thm. 4.15], one might ask for this stronger notion of
![]() $k$
-formality among hyperpolygonal arrangements. Computational evidence for further non-free hyperpolygonal arrangements suggests the following.
$k$
-formality among hyperpolygonal arrangements. Computational evidence for further non-free hyperpolygonal arrangements suggests the following.
Conjecture 5.3. For any
![]() $n \in {\mathbb N}$
,
$n \in {\mathbb N}$
,
![]() ${\mathscr H}_n$
is
${\mathscr H}_n$
is
![]() $k$
-formal for any
$k$
-formal for any
![]() $k$
.
$k$
.
6. Rank-generating functions of the poset of regions
Let
![]() $\mathscr A{\kern1.5pt}$
be a hyperplane arrangement in the real vector space
$\mathscr A{\kern1.5pt}$
be a hyperplane arrangement in the real vector space
![]() $V={\mathbb R}^\ell$
. A region of
$V={\mathbb R}^\ell$
. A region of
![]() $\mathscr A{\kern1.5pt}$
is a connected component of the complement
$\mathscr A{\kern1.5pt}$
is a connected component of the complement
![]() $M({\mathscr A}{\kern2pt}) :\!= V \setminus \cup _{H \in {\mathscr A}}H$
of
$M({\mathscr A}{\kern2pt}) :\!= V \setminus \cup _{H \in {\mathscr A}}H$
of
![]() $\mathscr A$
. Let
$\mathscr A$
. Let
![]() ${\mathscr R}{\kern2pt} :\!= {\mathscr R}({\mathscr A}{\kern1.5pt})$
be the set of regions of
${\mathscr R}{\kern2pt} :\!= {\mathscr R}({\mathscr A}{\kern1.5pt})$
be the set of regions of
![]() $\mathscr A$
. For
$\mathscr A$
. For
![]() $R, R' \in {\mathscr R}$
, we let
$R, R' \in {\mathscr R}$
, we let
![]() ${\mathcal S}(R,R')$
denote the set of hyperplanes in
${\mathcal S}(R,R')$
denote the set of hyperplanes in
![]() $\mathscr A{\kern1.5pt}$
separating
$\mathscr A{\kern1.5pt}$
separating
![]() $R$
and
$R$
and
![]() $R'$
. Then with respect to a choice of a fixed base region
$R'$
. Then with respect to a choice of a fixed base region
![]() $B$
in
$B$
in
![]() $\mathscr R$
, we can partially order
$\mathscr R$
, we can partially order
![]() $\mathscr R$
as follows:
$\mathscr R$
as follows:
Endowed with this partial order, we call
![]() $\mathscr R$
the poset of regions of
$\mathscr R$
the poset of regions of
![]() $\mathscr A{\kern1.5pt}$
(with respect to
$\mathscr A{\kern1.5pt}$
(with respect to
![]() $B$
) and denote it by
$B$
) and denote it by
![]() $P({\mathscr A}, B)$
. This is a ranked poset of finite rank, where
$P({\mathscr A}, B)$
. This is a ranked poset of finite rank, where
![]() $\operatorname {rk}(R) :\!= |{\mathcal S}(B,R)|$
, for
$\operatorname {rk}(R) :\!= |{\mathcal S}(B,R)|$
, for
![]() $R$
a region of
$R$
a region of
![]() $\mathscr A$
, [Reference Edelman16, Prop. 1.1]. The rank-generating function of
$\mathscr A$
, [Reference Edelman16, Prop. 1.1]. The rank-generating function of
![]() $P({\mathscr A}, B)$
is defined to be the following polynomial in
$P({\mathscr A}, B)$
is defined to be the following polynomial in
![]() ${\mathbb Z}_{\ge 0}[t]$
${\mathbb Z}_{\ge 0}[t]$
This poset along with its rank-generating function was introduced by Edelman [Reference Edelman16].
Thanks to work of Björner, Edelman, and Ziegler [Reference Björner, Edelman and Ziegler8, Thm. 4.4] (see also Paris [Reference Paris37]), respectively Jambu and Paris [Reference Jambu and Paris27, Prop. 3.4, Thm. 6.1], in case of a real arrangement
![]() $\mathscr A{\kern1.5pt}$
which is supersolvable, respectively inductively factored, there always exists a suitable base region
$\mathscr A{\kern1.5pt}$
which is supersolvable, respectively inductively factored, there always exists a suitable base region
![]() $B$
so that
$B$
so that
![]() $\zeta (P({\mathscr A},B);\, t)$
admits a multiplicative decomposition which is determined by the exponents of
$\zeta (P({\mathscr A},B);\, t)$
admits a multiplicative decomposition which is determined by the exponents of
![]() $\mathscr A$
, that is
$\mathscr A$
, that is
where
![]() $\{e_1, \ldots, e_\ell \} = \exp {\mathscr A}$
is the set of exponents of
$\{e_1, \ldots, e_\ell \} = \exp {\mathscr A}$
is the set of exponents of
![]() $\mathscr A$
.
$\mathscr A$
.
Quite remarkably, many classical real arrangements do satisfy the factorization identity (6.1), the most prominent ones being Coxeter arrangements.
Let
![]() $W = (W,S)$
be a Coxeter group with associated reflection arrangement
$W = (W,S)$
be a Coxeter group with associated reflection arrangement
![]() ${\mathscr A} = {\mathscr A}{\kern1.5pt}(W)$
which consists of the reflecting hyperplanes of the reflections in
${\mathscr A} = {\mathscr A}{\kern1.5pt}(W)$
which consists of the reflecting hyperplanes of the reflections in
![]() $W$
in the real space
$W$
in the real space
![]() $V={\mathbb R}^n$
, where
$V={\mathbb R}^n$
, where
![]() $|S| = n$
. The Poincaré polynomial
$|S| = n$
. The Poincaré polynomial
![]() $W(t)$
of the Coxeter group
$W(t)$
of the Coxeter group
![]() $W$
is the polynomial in
$W$
is the polynomial in
![]() ${\mathbb Z}[t]$
defined by
${\mathbb Z}[t]$
defined by
where
![]() $\ell$
is the length function of
$\ell$
is the length function of
![]() $W$
with respect to
$W$
with respect to
![]() $S$
. Then
$S$
. Then
![]() $W(t)$
coincides with the rank-generating function of the poset of regions
$W(t)$
coincides with the rank-generating function of the poset of regions
![]() $\zeta (P({\mathscr A}{\kern2pt},B);\, t)$
of the underlying reflection arrangement
$\zeta (P({\mathscr A}{\kern2pt},B);\, t)$
of the underlying reflection arrangement
![]() ${\mathscr A}{\kern2pt} = {\mathscr A}{\kern1.5pt}(W)$
with respect to
${\mathscr A}{\kern2pt} = {\mathscr A}{\kern1.5pt}(W)$
with respect to
![]() $B$
being the dominant Weyl chamber of
$B$
being the dominant Weyl chamber of
![]() $W$
in
$W$
in
![]() $V$
; see [Reference Björner, Edelman and Ziegler8] or [Reference Jambu and Paris27].
$V$
; see [Reference Björner, Edelman and Ziegler8] or [Reference Jambu and Paris27].
The following factorization of
![]() $W(t)$
is due to Solomon [Reference Solomon40]:
$W(t)$
is due to Solomon [Reference Solomon40]:
where
![]() $\{e_1, \ldots, e_n\}$
is the set of exponents of
$\{e_1, \ldots, e_n\}$
is the set of exponents of
![]() $W$
, that is, the set of exponents of
$W$
, that is, the set of exponents of
![]() ${\mathscr A}{\kern1.5pt}(W)$
; see also [Reference Macdonald29]. So by the comments above, (6.3) coincides with the factorization in (6.1).
${\mathscr A}{\kern1.5pt}(W)$
; see also [Reference Macdonald29]. So by the comments above, (6.3) coincides with the factorization in (6.1).
Let
![]() $W$
be a Coxeter group again with reflection arrangement
$W$
be a Coxeter group again with reflection arrangement
![]() ${\mathscr A} = {\mathscr A}{\kern1.5pt}(W)$
, let
${\mathscr A} = {\mathscr A}{\kern1.5pt}(W)$
, let
![]() $X$
be a member of the intersection lattice
$X$
be a member of the intersection lattice
![]() $L({\mathscr A}{\kern1.5pt})$
, and consider the restricted reflection arrangement
$L({\mathscr A}{\kern1.5pt})$
, and consider the restricted reflection arrangement
![]() ${\mathscr A}^{{\kern1.5pt}X}$
. In general,
${\mathscr A}^{{\kern1.5pt}X}$
. In general,
![]() ${\mathscr A}^{{\kern1.5pt}X}$
is no longer a reflection arrangement. It was shown in [Reference Möller and Röhrle32, Thm. 1.3] that there always exists a suitable base region
${\mathscr A}^{{\kern1.5pt}X}$
is no longer a reflection arrangement. It was shown in [Reference Möller and Röhrle32, Thm. 1.3] that there always exists a suitable base region
![]() $B$
of
$B$
of
![]() ${\mathscr A}^{{\kern1.5pt}X}$
in
${\mathscr A}^{{\kern1.5pt}X}$
in
![]() $X$
so that also
$X$
so that also
![]() $\zeta (P({\mathscr A}^{{\kern1.5pt}X},B);\, t)$
satisfies (6.1) provided
$\zeta (P({\mathscr A}^{{\kern1.5pt}X},B);\, t)$
satisfies (6.1) provided
![]() $W$
is not of type
$W$
is not of type
![]() $E_8$
. In case
$E_8$
. In case
![]() $W$
is of type
$W$
is of type
![]() $E_8$
, then
$E_8$
, then
![]() $\zeta (P({\mathscr A}^{{\kern1.5pt}X},B);\, t)$
satisfies (6.1) provided
$\zeta (P({\mathscr A}^{{\kern1.5pt}X},B);\, t)$
satisfies (6.1) provided
![]() $X$
has rank at most 3 with only two exceptions or
$X$
has rank at most 3 with only two exceptions or
![]() ${\mathscr A}^{{\kern1.5pt}X} \cong (E_8,D_4)$
${\mathscr A}^{{\kern1.5pt}X} \cong (E_8,D_4)$
Moreover, also the rank-generating function of the poset of regions
![]() $\zeta (P({\mathscr A}_{\mathcal I},B);\, t)$
for a so-called ideal arrangement
$\zeta (P({\mathscr A}_{\mathcal I},B);\, t)$
for a so-called ideal arrangement
![]() ${\mathscr A}_{\mathcal I}$
also obeys the factorization identity (6.1). Ideal arrangements
${\mathscr A}_{\mathcal I}$
also obeys the factorization identity (6.1). Ideal arrangements
![]() ${\mathscr A}_{\mathcal I}$
stem from ideals
${\mathscr A}_{\mathcal I}$
stem from ideals
![]() $\mathcal I$
in the poset of positive roots associated with a Weyl group; see [Reference Sommers and Tymoczko41], [Reference Abe, Barakat, Cuntz, Hoge and Terao1], [Reference Röhrle38], and [Reference Abe, Horiguchi, Masuda, Murai and Sato3].
$\mathcal I$
in the poset of positive roots associated with a Weyl group; see [Reference Sommers and Tymoczko41], [Reference Abe, Barakat, Cuntz, Hoge and Terao1], [Reference Röhrle38], and [Reference Abe, Horiguchi, Masuda, Murai and Sato3].
We close with a comment on the rank-generating function of the poset of regions of the free hyperpolygonal arrangements
![]() ${\mathscr H}_n$
.
${\mathscr H}_n$
.
Acknowledgments
We are grateful to T. Hoge and S. Wiesner for helpful discussions on material in this paper. The research of this work was supported in part by the DFG (Grant #RO 1072/25-1 (project number: 539865068) to G. Röhrle).