Inductive and projective limits of normed spaces

Extract

Let {U_i, U_ij} be an inductive system of normed linear spaces U_i and continuous linear maps u_ij; U_j → U_i. (We write j ≺ i if u_ij: U_j → U_i.) An inductive limit of the system with respect to a class 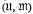of spaces A in 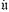and maps f in 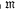is a space U_u in U_u and a system u_i → U_u of maps in 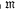such that (i) 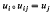whenever j ≺ i, and that (ii) if A is any space in 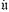and f_i: U_i → A is any system of maps in 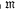for which 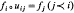then there is a unique map f: U_u → A in 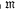such that f_i = f_o u_i for each i. If 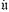is the class of all vector spaces and 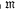is the class of linear maps, we obtain the algebraic inductive limit, which we denote simply by U. The usual choice is to take 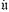to be the class of locally convex spaces and 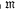the class of continuous linear maps; the inductive limit U_L then always exists [1, § 16 C]. If 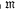is again the continuous linear mappings but 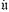contains only normed spaces, the corresponding inductive limit U_N may not always exist. However, if in addition we require that 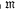contains just contractions (norm-decreasing linear mappings), then an inductive limit U_c will exist if every u_ij is a contraction [2]. We shall give a condition under which these limits coincide (as far as possible), and consider the corresponding condition for projective limits.