Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-15T04:01:07.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for the Schatten P-norm

Published online by Cambridge University Press:  18 May 2009

Fuad Kittaneh
Fuad Kittaneh
Affiliation:
Department of MathematicsUnited Arab Emirates Univ.P.O. Box 15551, Al-Ain, U.A.E.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a separable, infinite dimensional complex Hilbert space, and let B(H) denote the algebra of all bounded linear operators on H. Let K(H) denote the ideal of compact operators on H. For any compact operator A let |A|=(A*A)1,2 and S1(A), s2(A),… be the eigenvalues of |A| in decreasing order and repeatedaccording to multiplicity. If, for some 1<p<∞, 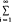si(A)p <∞, we say that A is in the Schatten p-class Cp and ∥A∥p=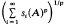1/p is the p-norm of A. Hence, C1 is the trace class, C2 is the Hilbert–Schmidt class, and C∞ is the ideal of compact operators K(H).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 26 , Issue 2 , July 1985 , pp. 141 - 143
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Helton, J. and Howe, R., Traces of commutators of integral operators. Ada Math. 135 (1975), 271–305.Google Scholar
2.Ringrose, J. R., Compact non-self-adjoint operators (Van Nostrand Reinhold Co., 1971).Google Scholar
3.Rosenblum, M., On the operator equation BX–XA = Q. Duke Math. J. 23 (1956), 263–270.CrossRefGoogle Scholar
4.Simon, B., Trace ideals and their applications (Cambridge University Press, 1979).Google Scholar