Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T22:38:34.954Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals involving E-functions

Published online by Cambridge University Press:  18 May 2009

C. B. Rathie
C. B. Rathie
Affiliation:
Maharana Bhupal College, Udaipur
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper three integrals involving E-functions are evaluated in terms of E-functions. The formulae to be established are:

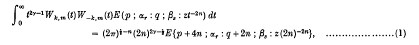
where n is a positive integer, | args z < π, R(γ ± m ÷ ½) > 0, αρ+ν = (2γ + ν)/2n (ν = 1, 2, …, 2n), αρ+2n+i = (γ + m - ½ + i)/n, αρ+3n+i = (γ - m - ½ + i)/n, βα+i = (γ + κ + i)/n, βα+ν+i = (γ - κ + i)/n(i = 1, 2, …, n).

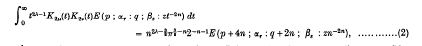
where n is a positive integer, |arg z| < π, R(λ±μ±ν) > 0, αp+i+1 = (λ + μ + ν + i)/n, αp+n+i+1 = (λ - μ + ν + i)/n, αp+2n+i+1 = (λ + μ - ν + i)/n, αp+3n+i+1 = (λ - μ - ν + i)/n (i = 0, 1, 2, …, n - 1), βa+i+1 = (2λ + j)/2n (j = 0, 1, 2, …, 2n - 1).

where n is a positive integer, R(λ) > ½, |arg z| < π, αp+i+1 = (2λ - 1 + i)/2n (i = 0, 1, 2, …, 2n-1), βq+j+1 = (λ + μ j)/n, βq+n+j+1 = (λ - μ + j)/n (j = 0, 1, 2, …, n-1).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 4 , September 1960 , pp. 186 - 187
Copyright
Copyright © Glasgow Mathematical Journal Trust 1960

References

1.MacRobert, T. M., Functions of a complex variable, 4th edition (1954).Google Scholar
2.Titchmarsh, E. C., Some integrals involving Bessel functions, J. London Math. Soc. 2 (1927), p. 98.Google Scholar