Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saxena, R.K.
1966.
On the Reducibility of Appelles Function F4*.
Canadian Mathematical Bulletin,
Vol. 9,
Issue. 2,
p.
215.
Maloo, H. B.
1966.
Integrals involving products of Bessel function and Meijer's G-function.
Monatshefte f�r Mathematik,
Vol. 70,
Issue. 2,
p.
127.
Maloo, H. B.
1966.
Integrals involving products of Bessel function and Meijer's G-function II.
Monatshefte f�r Mathematik,
Vol. 70,
Issue. 4,
p.
349.
Saxena, R. K.
1966.
Integrals involving products of Bessel functions ? II.
Monatshefte f�r Mathematik,
Vol. 70,
Issue. 2,
p.
161.
Pathan, M.A.
1979.
On a transformation of a general hypergeometric series of four variables.
Indagationes Mathematicae (Proceedings),
Vol. 82,
Issue. 1,
p.
171.
Prudnikov, A. P.
Brychkov, Yu. A.
and
Marichev, O. I.
1991.
Evaluation of integrals and the mellin transform.
Journal of Soviet Mathematics,
Vol. 54,
Issue. 6,
p.
1239.

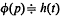 will be used to denote the classical Laplace integral relation
will be used to denote the classical Laplace integral relation
