Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T06:49:59.810Z Has data issue: false hasContentIssue false
  • English
  • Français

IRREDUCIBLE HARISH CHANDRA MODULES OVER THE DERIVATION ALGEBRAS OF RATIONAL QUANTUM TORI

Published online by Cambridge University Press:  25 February 2013

GENQIANG LIU  and
KAIMING ZHAO
GENQIANG LIU
Affiliation:
College of Mathematics and Information Science, Henan University, Kaifeng 475004, China e-mail: liugenqiang@amss.ac.cn
KAIMING ZHAO
Affiliation:
Department of Mathematics, Wilfrid Laurier University, Waterloo, ON N2L 3C5, Canada, and College of Mathematics and Information Science, Hebei Normal (Teachers) University, Shijiazhuang, Hebei 050016, China e-mail: kzhao@wlu.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let d be a positive integer, q=(qij)d×d be a d×d matrix, ℂq be the quantum torus algebra associated with q. We have the semidirect product Lie algebra 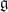$\mathfrak{g}$=Der(ℂq)⋉Z(ℂq), where Z(ℂq) is the centre of the rational quantum torus algebra ℂq. In this paper, we construct a class of irreducible weight 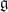$\mathfrak{g}$-modules 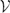$\mathcal{V}$α (V,W) with three parameters: a vector α∈ℂd, an irreducible 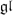$\mathfrak{gl}$d-module V and a graded-irreducible 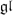$\mathfrak{gl}$N-module W. Then, we show that an irreducible Harish Chandra (uniformaly bounded) 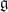$\mathfrak{g}$-module M is isomorphic to 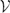$\mathcal{V}$α(V,W) for suitable α, V, W, if the action of Z(ℂq) on M is associative (respectively nonzero).

Keywords

17B1017B2017B6517B6617B68
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 3 , September 2013 , pp. 677 - 693
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Allison, B., Azam, S., Berman, S., Gao, Y. and Pianzola, A., Extended affine Lie algebras and their root systems, Memoirs of the American Mathematical Society 126, vol. 605 (AMS, Providence, RI, 1997).Google Scholar
2.Allison, B., Berman, S., Faulkner, J. and Pianzola, A., Realization of graded-simple algebras as loop algebras, Forum Mathematicum 20(2008), 395–432.CrossRefGoogle Scholar
3.Berman, S., Gao, Y. and Krylyuk, Y. S., Quantum tori and the structure of elliptic quasi-simple Lie algebras, J. Funct. Anal. 135(1996), 339–389.CrossRefGoogle Scholar
4.Billig, Y., A category of modules for the full toroidal Lie algebra, Int. Math. Res. Not. (2006), Art. ID 68395, 46.Google Scholar
5.Billig, Y., Jet modules, Canad. J. Math. 59 (4) (2007), 712–729.CrossRefGoogle Scholar
6.Billig, Y. and Lau, M., Thin coverings of modules, J. Algebra 316(2007), 147–173.Google Scholar
7.Billig, Y., Molev, A. and Zhang, R., Differential equations in vertex algebras and simple modules for the Lie algebra of vector fields on a torus, Adv. Math. 218 (6) (2008), 1972–2004.CrossRefGoogle Scholar
8.Billig, Y. and Zhao, K., Weight modules over exp-polynomial Lie algebras, J. Pure Appl. Algebra, 191 (1–2) (2004), 23–42.CrossRefGoogle Scholar
9.Eswara Rao, S., Irreducible representations of the Lie-algebra of the diffeomorphisms of a d-dimensional torus, J. Algebra 182 (2) (1996), 401–421.Google Scholar
10.Eswara Rao, S., Partial classification of modules for Lie- algebra of diffeomorphisms of d-dimensional torus, J. Math. Phys., 45 (8) (2004), 3322–3333.Google Scholar
11.Eswara Rao, S., Irreducible representations for Toroidal Lie algebras, J. Pure Appl. Algebra 202 (2005), 102–117.Google Scholar
12.Eswara Rao, S. and Jiang, C., Classification of irreducible integrable representations for the full toroidal Lie algebras, J. Pure Appl. Algebra 200(1–2) (2005), 71–85.CrossRefGoogle Scholar
13.Gracia-Bondia, J. M., Vasilly, J. C. and Figueroa, H., Elements of non- commutative geometry (Birkhauser Advanced Texts, Birkhauser Verlag, Basel, Switzerland, 2001).CrossRefGoogle Scholar
14.Guo, X., Liu, G. and Zhao, K., Irreducible Harish Chandra modules over extended Witt algebras, Ark. Mat. doi:10.1007/s11512-012-0173-9.Google Scholar
15.Guo, X. and Zhao, K., Irreducible weight modules over Witt algebras, Proc. Amer. Math. Soc. 139(2011), 2367–2373.CrossRefGoogle Scholar
16.Jacbson, N., Basic algebra, II (W. H. Freeman and Company, San Francisco, CA, 1980).Google Scholar
17.Kac, V. and Raina, A., Bombay lectures on highest weight representations of infinite dimensional Lie algebras (World Sci., Singapore, 1987).Google Scholar
18.Larsson, T. A., Multi-dimensional Virasoro algebra, Phys. Lett. B 231 (1989), 94–96.Google Scholar
19.Larsson, T. A., Central and non-central extensions of multi-graded Lie algebras, J. Phys. A 25 (1992), 1177–1184.CrossRefGoogle Scholar
20.Larsson, T. A., Conformal fields: A class of representations of Vect (N), Int. J. Mod. Phys. A 7 (1992), 6493–6508.CrossRefGoogle Scholar
21.Larsson, T. A., Lowest energy representations of non-centrally extended diffeomorphism algebras, Commun. Math. Phys. 201(1999), 461–470.CrossRefGoogle Scholar
22.Larsson, T. A., Extended diffeomorphism algebras and trajectories in jet space, Commun. Math. Phys. 214(2000), 469–491.Google Scholar
23.Liu, G. and Zhao, K., Irreducible modules over the derivation algebras of rational quantum tori, J. Algebra 340(2011), 28–34.Google Scholar
24.Lu, R. and Zhao, K., Classification of irreducible weight modules over higher rank Virasoro algebras, Adv. Math. 201 (2) (2006), 630–656.CrossRefGoogle Scholar
25.Mathieu, O., Classification of Harish Chandra modules over the Virasoro Lie algebra, Invent. Math. 107 (2) (1992), 225–234.CrossRefGoogle Scholar
26.Mathieu, O., Classification of irreducible weight modules, Ann. Inst. Fourier (Grenoble) 50 (2) (2000), 537–592.Google Scholar
27.Mazorchuk, V., On simple mixed modules over the Virasoro algebra, Mat. Stud. 22 (2) (2004), 121–128.Google Scholar
28.Mazorchuk, V., Lectures on $\mathfrak{sl}_2(\mathbb{C})$-modules (Imperial College Press, 2010).Google Scholar
29.Marzuchuk, V. and Zhao, K., Supports of weight modules over Witt algebras, Proc. R. Soc. Edinburgh A 141 (1) (2011), 155–170.Google Scholar
30.Neeb, K., On the classification of rational quantum tori and the structure of their automorphism groups, Canad. Math. Bull. 51 (2) (2008), 261–282.CrossRefGoogle Scholar
31.Ramos, E., Sah, C. H. and Shrock, R. E., Algebras of diffeomorphisms of the N-torus, J. Math. Phys. 31 (8) (1990), 1805–1816.CrossRefGoogle Scholar
32.Shen, G., Graded modules of graded Lie algebras of Cartan type. I. Mixed products of modules, Sci. Sinica Ser. A 29 (6) (1986), 570–581.Google Scholar
33.Zhao, K., Weight modules over generalized Witt algebras with 1-dimensional weight spaces, Forum Math. 16 (5) (2004), 725–748.Google Scholar
34.Zhao, K., The q-Virasoro-like algebra, J. Algebra (1997), 506–512.Google Scholar