Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T07:10:36.205Z Has data issue: false hasContentIssue false
  • English
  • Français

ISOMORPHIC INDUCED MODULES AND DYNKIN DIAGRAM AUTOMORPHISMS OF SEMISIMPLE LIE ALGEBRAS

Part of: Lie algebras and Lie superalgebras Algebraic combinatorics

Published online by Cambridge University Press:  21 July 2015

JÉRÉMIE GUILHOT  and
CÉDRIC LECOUVEY
JÉRÉMIE GUILHOT
Affiliation:
Laboratoire de Mathématiques et Physique Théorique, (UMR CNRS 7350) Université François-Rabelais, Tours Fédération de Recherche Denis Poisson. e-mail: jeremie.guilhot@lmpt.univ-tours.fr; cedric.lecouvey@lmpt.univ-tours.fr
CÉDRIC LECOUVEY
Affiliation:
Laboratoire de Mathématiques et Physique Théorique, (UMR CNRS 7350) Université François-Rabelais, Tours Fédération de Recherche Denis Poisson. e-mail: jeremie.guilhot@lmpt.univ-tours.fr; cedric.lecouvey@lmpt.univ-tours.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a simple Lie algebra 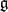$\mathfrak{g}$ and 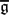$\overline{\mathfrak{g}}$ ⊂ 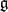$\mathfrak{g}$ a Levi subalgebra. Two irreducible 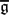$\overline{\mathfrak{g}}$-modules yield isomorphic inductions to 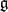$\mathfrak{g}$ when their highest weights coincide up to conjugation by an element of the Weyl group W of 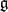$\mathfrak{g}$ which is also a Dynkin diagram automorphism of 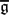$\overline{\mathfrak{g}}$. In this paper, we study the converse problem: given two irreducible 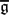$\overline{\mathfrak{g}}$-modules of highest weight μ and ν whose inductions to 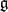$\mathfrak{g}$ are isomorphic, can we conclude that μ and ν are conjugate under the action of an element of W which is also a Dynkin diagram automorphism of 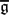$\overline{\mathfrak{g}}$? We conjecture this is true in general. We prove this conjecture in type A and, for the other root systems, in various situations providing μ and ν satisfy additional hypotheses. Our result can be interpreted as an analogue for branching coefficients of the main result of Rajan [6] on tensor product multiplicities.

MSC classification

Primary: 05E05: Symmetric functions and generalizations
Secondary: 05E10: Combinatorial aspects of representation theory 17B20: Simple, semisimple, reductive (super)algebras 17B22: Root systems
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 1 , January 2016 , pp. 187 - 203
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1.Bourbaki, N., Groupes et algèbres de Lie, Chapitres 4,5,6, (Hermann, Paris, 1968).Google Scholar
2.Duan, H., On the inverse Kostka matrix, J. Comb. Theory Ser. A 103 (2) (2003), 363–376.CrossRefGoogle Scholar
3.Goodman, G. and Wallach, N. R., Representations and invariants of the classical groups (Cambridge University Press, Cambridge, 1998).Google Scholar
4.Humphreys, J. E., Reflection groups and Coxeter groups, Cambridge studies in advance mathematics, vol. 29 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
5.Littlewood, D. E., The theory of group characters and matrix representations of groups (Reprint of the second (1950) edition. AMS Chelsea Publishing, Providence, RI, 2006).CrossRefGoogle Scholar
6.Rajan, C. S., Unique decomposition of tensor products of irreducible representations of simple algebraic groups, Ann. Math. 160 (2) (2004), 683–704.CrossRefGoogle Scholar
7.Serre, J. P., Complex semisimple Lie algebras (Reprint of the 1987 edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2001).CrossRefGoogle Scholar
8.Venkatesh, R. and Viswanath, S., Unique factorization of tensor products for Kac–Moody algebras, Adv. in Math. 231 (6) (2012), 3162–3171.CrossRefGoogle Scholar
9.Wildon, M., Character values and decomposition matrices of symmetric groups, J. Algebra 319 (8) (2008), 3382–3397.CrossRefGoogle Scholar