Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chō, Muneo
1988.
Joint spectra of commuting normal operators on Banach spaces.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 3,
p.
339.
Wrobel, Volker
1988.
Joint spectra and joint numerical ranges for pairwise commuting operators in Banach spaces.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 2,
p.
145.
Haupt, Herbert A.
1989.
Drugs in Athletics.
Clinics in Sports Medicine,
Vol. 8,
Issue. 3,
p.
561.
Chō, Muneo
1990.
Semi-normal operators on uniformly smooth Banach spaces.
Glasgow Mathematical Journal,
Vol. 32,
Issue. 3,
p.
273.
LI, CHI-KWONG
and
POON, YIU-TUNG
2009.
SPECTRUM, NUMERICAL RANGE AND DAVIS-WIELANDT SHELL OF A NORMAL OPERATOR.
Glasgow Mathematical Journal,
Vol. 51,
Issue. 1,
p.
91.

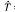 = (T
= (T