Kato’s main conjecture for potentially ordinary primes

Abstract

In this paper, we prove Kato’s main conjecture for 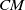$CM$ modular forms for primes of potentially ordinary reduction under certain hypotheses on the modular form.

1. Introduction

Let $p\ge 5$ be a prime and $E$ be an elliptic curve defined over $\mathbb{Q}$ with complex multiplication by the ring of integers of an imaginary quadratic field $K$ . If we consider the $p$ -primary Selmer group of $E$ along the unique $\mathbb{Z}_p$ -extension of $\mathbb{Q}$ , it is a natural question to ask whether the characteristic ideal of the Pontryagin dual of this Selmer group can be related to a $p$ -adic $L$ -function interpolating the $L$ -function associated with $E$ . For primes of good reduction, the answer to this question is positive. The ordinary case was solved by Rubin [11] and the supersingular case by Pollack and Rubin [13]. Lei generalized their works for general modular forms and supersingular primes [8].

A natural next step would be to consider the potentially ordinary case. One of the main problems in considering potentially ordinary primes is that the definition of the $p$ -adic $L$ -function becomes more involved. The construction following Amice-Velu [1] and Vishik [14] as, for example, given in [7, Theorem 16.2] relies on the fact that the $L$ -function associated with our modular form has a nontrivial Euler factor at $p$ . If $p$ is a potentially ordinary prime (i.e., a bad prime), then this Euler factor is trivial. Delbourgo constructed in [3] $p$ -adic $L$ -functions for elliptic curves at potentially ordinary primes by twisting the representation given by the action on $G_{\mathbb{Q}}$ on $E[p^\infty ]$ by a character of finite order. The goal of the present article is to construct a $p$ -adic $L$ -function for modular forms that are potentially ordinary at $p$ and to prove that it describes the characteristic ideal of the Pontryagin dual of the classical Selmer group in the sense of an Iwasawa main conjecture. A main building block will be to mimic Delbourgo’s idea in Section 5 to construct our $p$ -adic $L$ -functions. The second main building block in the present paper is to use the “classical” Iwasawa main conjecture for imaginary quadratic fields proved by Rubin to show that the $p$ -adic $L$ -function construced in Section 5 actually satisfies an Iwasawa main conjecture [11].

As in the elliptic curve case (see [13]), we will only consider imaginary quadratic fields $K$ of class number one. This makes it easier to work with the Euler system of elliptic units and ensures that there is exactly one prime above $p$ in the unique $\mathbb{Z}_p^2$ -extension of $K$ .

We will say that a modular form is defined over a field $L$ if all its Fourier coefficients lie in $L$ . Let $f$ be a newform defined over $\mathbb{Q}$ of level $N$ , weight $k$ , and nebentypus $\psi$ . Let $p\ge 5$ be a prime of potentially ordinary reduction for $f$ , that is, $p$ is a prime of bad reduction over $\mathbb{Q}$ and becomes ordinary over some finite extension (see Section 3 for a precise definition). In fact, we will always assume that we obtain good ordinary reduction over $\mathbb{Q}_p(\mu _p)$ . This assumption will allow us to define a twist $\tilde{f}$ of $f$ that is defined over $\mathbb{Q}$ and that has a nontrivial Euler factor at $p$ .

Let $\phi$ be a Hecke character of $K$ of infinity type $(1-k,0)$ .1 We say that a modular form $f$ has complex multiplication if $L(f,s)=L(\phi,s)$ for some Hecke character over $K$ as described above. We will always assume that $f$ has CM.

Let $\pi$ be a generator for a prime lying above $p$ in $K$ and denote the completion of $K$ at $\pi$ by $K_{\pi }$ . We will write $\mathcal{O}$ and $\mathcal{O}_{\pi }$ for the ring of integers in $K$ and $K_{\pi }$ , respectively. We let $V=V(f)$ be the $p$ -adic $G_{\mathbb{Q}}$ -representation associated with $f$ by Deligne, that is, if $l\neq p$ is a prime coprime to the level of $f$ , then $\textrm{Frob}_l$ acts with trace $a_l$ on $V$ , where $a_l$ is the Fourier coefficient of $f$ at $l$ . In general, this representation is defined over the smallest field over $\mathbb{Q}_p$ containing all the coefficients of $f$ . In our setting, $V$ will always be a two-dimensional representation over $\mathbb{Q}_p$ . In the course of the paper, we will fix a sublattice $T\subset V$ that is Galois stable.

We define $A=V/T(1)$ . To ensure that the ring of endomorphisms of $A$ is canonically isomorphic to $\mathcal{O}_{\pi }$ , we will always assume that the Hecke character $\phi$ takes values in $K$ and that $p$ is either inert or ramified in $K$ .

Let $G_K$ be the absolute Galois group of $K$ and let

\begin{align*} \rho \colon G_K\to (\mathcal{O}_{\pi })^{\times }=\textrm{Aut}(A) \end{align*}

be the natural representation of $G_K$ on $A$ . It can be shown that $\rho$ factors through $\textrm{Gal}(K(\mathfrak{f}p^\infty )/K)$ , where $\mathfrak{f}$ is the conductor of $\phi$ and $K(\mathfrak{m})$ is the ray class field of $K$ to the modulus $\mathfrak{m}$ [7, Section 15]. If $f$ is associated with an elliptic curve $E/\mathbb{Q}$ with potentially ordinary (and bad) reduction at $p$ , then we have $\mathcal{K}=K(E[p^\infty ])=K(p^\infty )$ and $A=E[p^\infty ]$ . In any case, we have a decomposition $\textrm{Gal}(\mathcal{K}/K)\cong \mathbb{Z}_p^2\times \Delta$ for a finite group $\Delta$ . Note that this decomposition is canonical if $\vert \Delta \vert$ is coprime to $p$ .

Let us now give a precise definition of the Selmer groups we would like to consider. For any algebraic extension $F$ of $\mathbb{Q}$ , we define the Selmer group of $A$ over $F$ as follows:

\begin{align*} \textrm{Sel}(F,A)=\ker\!\left (H^1(F,A)\to \prod _v \frac{H^1(F_v,A)}{H^1_f(F_v,A)}\right ), \end{align*}

where the product runs over all primes in $F$ and $H^1_f(F_v,A)$ is defined as in [2, Section 3].

Before we state the main theorem of the article, let us summarize the technical assumptions we need to make on $f$ .

Assumption 1.1. We make the following assumptions on $K,p$ , and $f$ :

• • $f$ is defined over $\mathbb{Q}$ and has $CM$ by the Hecke character $\phi$ of $K$ .

• • $K$ is of class number one and $\phi$ takes values in $K$ .

• • The prime $p$ ramifies or is inert in $K$ .

• • The prime $p$ divides the level of $f$ and $f$ obtains good ordinary reduction over $\mathbb{Q}_p(\mu _p)$ .

• • Let $\mathcal{K}=K(\mathfrak{f}p^\infty )$ , where $\mathfrak{f}$ is the conductor of $\phi$ . Let $\Delta$ be the torsion subgroup of $\textrm{Gal}(\mathcal{K}/K)$ . The order $\vert \Delta \vert$ is coprime to $p$ .

• • None of the eigenvalues of $\varphi$ on $D_{\textrm{cycl}}(V(k))$ 2 is an integral power of $p$ .

• • The representation $\rho$ restricted to $\Delta$ is neither the inverse of the Teichmüller character nor the trivial character.

Note that all above conditions are satisfied for elliptic curves with potentially ordinary reduction at $p$ defined over $\mathbb{Q}$ (that are bad at $p$ ). So we are in particular able to consider elliptic curves such as the one given by $y^2+xy=x^3-x^2-2x-1$ (for this particular curve $p=7$ ). In the elliptic curve case, $p$ is always ramified in $K$ . For example, where $p$ is inert, see Section 3.

The condition that $p$ has to be inert or ramified is actually not really strong as it still allows us to take roughly half of all rational primes. The condition that we obtain good ordinary reduction over $\mathbb{Q}_p(\mu _p)$ basically says the power of $p$ that is allowed in the conductor of the Hecke character $\phi$ is not more than 1 and the condition that the order of $\Delta$ is coprime to $p$ is satisfied if $N(\mathfrak{q})-1$ is not divisible by $p$ for every ideal $\mathfrak{q}$ that divides $\mathfrak{f}$ . This still allows us to choose an infinite number of Hecke characters satisfying all the above conditions. As each Hecke character induces a CM modular form by [9], this shows that the family of $f$ satisfying the conditions is infinite.

1.1. The main theorem

Let $\mathbb{Q}_c$ be the cyclotomic $\mathbb{Z}_p$ -extension of $\mathbb{Q}$ . Let $\tau$ be a topological generator for $\textrm{Gal}(\mathbb{Q}_c/\mathbb{Q})$ and $T=\tau -1$ . Define $\Lambda =\mathbb{Z}_p[\![\textrm{Gal}(\mathbb{Q}_c/\mathbb{Q})]\!]=\mathbb{Z}_p[\![T]\!]$ . Then the Pontryagin dual $\textrm{Sel}(\mathbb{Q}_c,A)^\vee$ is a noetherian torsion $\Lambda$ -module. In the course of the paper, we will define a $p$ -adic $L$ -function $L_p(f)\in \mathbb{Z}_p[\![\textrm{Gal}(\mathbb{Q}(\mu _{p^\infty })/\mathbb{Q})]\!]$ interpolating the values of $L_{(p)}(f,\chi,1)$ , where $L_{(p)}(f,\chi,1)$ is the $L$ -function of $f$ twisted by a Dirichlet character $\chi$ and with the Euler factor at $p$ removed.

Theorem 1.2. Assume that all conditions of Assumption 1.1 hold. Let $L_p(f,\mathbb{Q})$ be the projection of $L_p(f)$ to $\Lambda$ . Then, we have

\begin{align*} \textrm{Char}_\Lambda (\textrm{Sel}(\mathbb{Q}_c,A)^\vee )=(L_p(f,\mathbb{Q})). \end{align*}

A Kato type main conjecture as described above was recently proved for modular motives [5] by Fouquet and Wan under the assumption that the corresponding residual representation $\overline{\rho }\colon G_{\mathbb{Q}} \to GL_2(\mathbb{F}_p)$ is absolutely irreducible. But not all the cases we consider satisfy this condition: Let $E$ be an elliptic curve with potentially ordinary (and bad) reduction at $p\ge 5$ and complex multiplication by $\mathcal{O}$ . As we assume that $E$ is defined over $\mathbb{Q}$ , it is immediate that $K$ has class number one and that $p$ is ramified in $K$ . Then the residual representation is given by the natural action of $G_{\mathbb{Q}}$ on $E[p]$ . Let $\mathfrak{p}$ be the unique prime above $p$ in $K$ . Then $E[\mathfrak{p}]\subsetneq E[p]$ is a Galois-invariant submodule. Hence, the residual representation cannot be absolutely irreducible.

2. Notation

We fix once and for all a normalized newform $f$ of weight $k\ge 2$ , level $N$ , and nebentypus $\psi '$ . We assume that the Fourier coefficients of $f$ lie in $\mathbb{Q}$ . We also fix a rational prime $p\ge 5$ and assume that $f$ has complex multiplication by a Hecke character $\phi$ of infinity type $(1-k,0)$ defined over the imaginary quadratic field $K$ . Let $\mathfrak{f}$ be the conductor of $\phi$ . In addition, we will frequently use the following (standard) notation for different fields:

• • For any integral ideal $\mathfrak{q}$ of $K$ , we denote by $K(\mathfrak{q})$ the ray class field of conductor $\mathfrak{q}$ .

• • $\mathcal{K}=K(\mathfrak{f}p^\infty )$ .

• • $K_{\infty }$ is the unique $\mathbb{Z}_p^2$ -extension of $K$ .

3. Preliminary results and conditions on modular forms

While the notion of potentially good primes is well known for elliptic curves, it might be less common for modular forms. Throughout this article, we will follow the convention of Kato.

Definition 3.1 ([7, Remark 12.7]). Let $f'$ be an arbitrary newform. Let $F_v$ be a finite extension of $\mathbb{Q}_p$ containing all coefficients of $f'$ and let $V_{f'}$ be the $p$ -adic representation associated with $f'$ by Deligne (i.e., for every prime $q\neq p$ that does not divide the level of $f'$ , $\textrm{Frob}_q$ acts with trace $a_q$ on $V_{f'}$ , where $a_q$ is the Fourier coefficient at $q$ ). The prime $p$ is a potentially good prime for $f'$ if there exists a finite extension $K'$ of $\mathbb{Q}_p$ such that $V_{f'}$ is crystalline as $G_{K'}$ -representation. We call $p$ potentially ordinary for $f'$ if there is a one-dimensional $G_{K'}$ -subrepresentation $V'_{f'}$ of $V_{f'}$ that is unramified as $G_{K'}$ -representation.

It is well known that an elliptic curve with complex multiplication is potentially good at every prime. We can prove the analogous result unconditionally for $CM$ forms with complex multiplication. We only state the proof here as the author was not able to find a reference.

Lemma 3.2. Let $f'$ be a $CM$ form and $l$ be any rational prime, then $f'$ has potentially good reduction at $l$ .

Proof. Let $\phi '$ be the Hecke character of $f'$ . Let $L$ be the smallest field containing all values of $\phi '$ . Let $w$ be a place coprime to $l$ in $L$ and $q$ a prime below it. Let $V_w$ be the $L_w$ -representation associated with $f'$ . Then $V_w\cong \textrm{Ind}_{\mathbb{Q}}^K(V_w(\phi '))$ , where $V_w(\phi ')$ is the $L_w$ -representation on which $G_K$ acts via $\phi '$ . This representation is only finitely ramified at each prime above $l$ . In particular, we can find a finite extension $K'/\mathbb{Q}_l$ such that $V_w$ is unramified as $G_{K'}$ -representation. According to [7, Remark 12.7] this implies that $l$ is a potentially good prime for $f'$ .

Remark 3.3. From now on we will always assume that a potentially ordinary prime is a prime dividing the level $N$ of $f'$ .

For an elliptic curve, it is known that if $E$ has potentially ordinary reduction at $p$ and $CM$ by $\mathcal{O}$ , then $p$ has to ramify in $K$ . For $CM$ newforms, this is only true under an additional assumption. The following lemma is also well known, but the author was not able to find a reference.

Lemma 3.4. Let $f'$ be a newform defined over $\mathbb{Q}$ with complex multiplication by $\mathcal{O}$ and trivial nebentypus. Assume that $p$ is a potentially ordinary prime. Then $p$ is ramified in $K$ .

Proof. Let $\psi =1$ be the nebentypus of $f'$ . As $f'$ is defined over $\mathbb{Q}$ , we see that the character $\psi$ can only take values in $\mathbb{Q}$ , so it is at most a quadratic character [9, Corollary 3.1]. Let $\eta$ be the Dirichlet character defined on $\mathbb{Z}$ that takes $a$ to the value $\phi '((a))/\inf (a)$ , where $\textrm{inf}$ denotes the infinity type of the Hecke character $\phi '$ associated with $f'$ .3 By definition, the conductors of $\eta$ and $\phi '$ are divisible by the same prime ideals (as we are only considering newforms we can assume that $\phi '$ is defined modulo its conductor). Furthermore, $\psi =\eta \psi '$ , where $\psi '$ is the nontrivial character of $\textrm{Gal}(K/\mathbb{Q})$ . It follows from the triviality of $\psi$ that the conductor of $\eta$ is only divisible by the primes ramifying in $K$ . Hence, the newform $f'$ has a conductor that is only divisible by these ramified primes and in fact $p$ is ramified in $K$ .

Remark 3.5. If the nebentypus $\psi$ of $f'$ is nontrivial, it has to be a quadratic character. Let $\eta$ be defined as in the proof of Lemma 3.4 . It follows from [ 9, Remark 2, section 3] that $\eta$ is trivial and that $\psi$ is induced by the character of $K$ . As we are only interested in newforms, we can again assume that the ideal $\mathfrak{m}$ Ribet uses in his construction of CM forms is indeed the conductor of the Grössencharacter $\phi$ . It then follows from [ 9, Theorem 3.4, Corollary 3.5 and Remark 3.5] that the discriminant of $K$ divides $N$ . But that does not allow us to conclude anything on the splitting behavior of $p$ in $K/\mathbb{Q}$ . Indeed, it is relatively easy to construct examples where $p$ is split or inert in $K/\mathbb{Q}$ and we will do so below.

In both examples, we will assume that $K\neq \mathbb{Q}(\sqrt{-1}),\mathbb{Q}(\sqrt{-3})$ is an imaginary quadratic field of class number one such that $\mathcal{O}^\times =\{\pm 1\}$ . We will also show that the modular forms we are constructing in these examples satisfy Assumption 1.1 .

• • Let $q$ be an odd prime that is inert in $K$ and let $g$ be a generator of $(\mathcal{O}/q)^\times$ . Let $k\ge 3$ be an odd integer and define the character $\phi '$ as follows. For every $a\in \mathcal{O}$ that is coprime to $p$ we put $\phi '((a))=(\!-\!1)^wa^{k-1}$ , where $w$ is given by the quantity $g^w\equiv a\mod q$ . Note that $g^{(q^2-1)/2}\equiv -1\mod q$ . Hence, the parity of $w$ does not depend on the choice of $a$ , and $\phi '$ is a well-defined Hecke character with values in $K$ . By definition, the conductor of $\phi '$ is $q$ . Let $f'$ be the newform associated with $\phi '$ by [ 9, Theorem 3.3 and Remark 3.5]. It remains to show that $f'$ is defined over $\mathbb{Q}$ . Let $\mathfrak{a}$ be a prime ideal in $K$ . If $\mathfrak{a}\cap \mathbb{Z}$ is inert in $K$ , then $\mathfrak{a}$ is generated by a prime $l\in \mathbb{Z}$ . As $l^{q-1}\equiv 1\mod q$ , we see that $w$ is even in this case and $\phi '(\mathfrak{a})=l^{k-1}\in \mathbb{Q}$ . If $\mathfrak{a}$ is ramified in $K$ , then $K=\mathbb{Q}(\sqrt{-p})$ , where $p$ is the unique prime below $\mathfrak{a}$ in $\mathbb{Q}$ . In this case, we get $\phi '(\mathfrak{a})=\pm p^{(k-1)/2}\in \mathbb{Q}$ . Assume now that $\mathfrak{a}\cap \mathbb{Z}=(\pi )\cap \mathbb{Z}$ is split, then $\pi \overline{\pi }=l$ for some rational prime $l$ . Let $\pi \equiv g^{w_1}\mod q$ and $\overline{\pi }\equiv g^{w_2}\mod q$ . It follows that $w_1$ and $w_2$ have the same parity, and we see that $\phi '(\overline{\mathfrak{a}})=\overline{\phi '(\mathfrak{a})}$ . So $\phi '(\mathfrak{a})+\phi '(\overline{\mathfrak{a}})\in \mathbb{Z}$ . Since $\phi '$ is multiplicative, $f'$ is indeed defined over $\mathbb{Q}$ .

• • Let $q$ be an odd prime that splits in $K/\mathbb{Q}$ . Recall that we denote the ring of integers of $K$ by $\mathcal{O}$ . Then, $(\mathcal{O}/q)^\times$ decomposes into two cyclic groups of order $q-1$ . There is a natural embedding:

  \begin{align*} \iota \colon (\mathbb{Z}/q)^\times \to (\mathcal{O}/q)^\times. \end{align*}
  Note that $C_q:=(\mathcal{O}/q)^\times/\iota ((\mathbb{Z}/q)^\times )$ is a cyclic group of order $q-1$ . We let $\overline{\eta }$ be the unique order $2$ character of $C_q$ . We then define $\eta$ as a character on $(\mathcal{O}/q)^\times$ given by $\eta (x)=\overline{\eta }(\overline{x})$ , where $\overline{x}$ denotes the image of $x$ in $C_q$ . Let again $k\ge 3$ be an odd integer and define $\phi ((a))=\eta (a)a^{k-1}$ for every $a$ that is corpime to $q$ . As before we can show that the modular form $f'$ associated with this, Grössencharacter is already defined over $\mathbb{Q}$ .

4. Description of the Selmer groups

For the rest of the paper, we assume that all conditions of Assumption 1.1 are satisfied. Recall also that we always assume that $p$ divides the level of our modular form $f$ . In particular, $p$ cannot be a good ordinary prime for $f$ . The main goal of this section is to establish a relation between the Selmer groups we are interested in and a quotient of the local units of the cyclotomic $\mathbb{Z}_p$ -extension of $K$ . Let us briefly recall the definition of the local finite conditions as given in [2, (3.7.1) and (3.7.2)].

Definition 4.1. Let $F$ be a number field. Let $K'$ be a finite extension of $\mathbb{Q}_p$ and let $\textbf{V}$ be a finite dimensional $K'$ -vector space with a continuous $G_F$ -action. Let $B_{\textrm{dr}}$ and $B_{\textrm{crys}}$ be the period rings defined by Fontaine (see also the summary in [ 2, section 1]). Let $v$ be a finite place of $F$ and let $F_v^{\textrm{ur}}$ be the maximal unramified extension of $F_v$ . Then, we define the local conditions:

\begin{align*} H^1_f(G_{F_v},\textbf{V})=\begin{cases}\textrm{ker}(H^1(G_{F_v},\textbf{V})\to H^1(G_{F^{\textrm{ur}}_{F_v}},\textbf{V}))\quad &(v,p)=1,\\[5pt] \textrm{ker}(H^1(G_{F_v},\textbf{V})\to H^1(G_{F_v}, \textbf{V}\otimes B_{\textrm{crys}}))\quad &v\mid p. \end{cases} \end{align*}

Let $\textbf{T}$ be a Galois-invariant lattice in $\textbf{V}$ and let $\textbf{A}=\textbf{V}/\textbf{T}$ . Then, there are natural maps:

\begin{align*} \iota _1\colon H^1(G_{F_v},\textbf{T})\to H^1(G_{F_v},\textbf{V}),\quad \iota _2\colon H^1(G_{F_v},\textbf{V})\to H^1(G_{F_v},\textbf{A}). \end{align*}

We define $H_f^1(G_{F_v},\textbf{T})$ as the preimage of $H^1_f(G_{F_v},\textbf{V})$ under $\iota _1$ and $H^1_f(G_{F_v},\textbf{A})$ as the image of $H^1_f(G_{F_v},\textbf{V})$ under $\iota _2$ .

If $v$ is coprime to $p$ , we furthermore define

\begin{align*} H^1_{\textrm{ur}}(G_{F_v},\textbf{A})=\textrm{ker}(H^1(G_{F_v},\textbf{A})\to H^1(G_{F^{\textrm{ur}}_{F_v}},\textbf{A})). \end{align*}

It is well known that $H^1_{\textrm{ur}}(G_{F_v},\textbf{A})=H^1_f(G_{F_v},\textbf{A})$ if $\textbf{V}$ is unramified as $G_{F_v}$ -module (see [ 12, Lemma 3.5]).

Recall that $V$ is the representation associated with $f$ by Deligne. We now go back to the special case $\textbf{V}=V(1)$ , $\textbf{T}=T(1)$ and $\textbf{A}=A=V/T(1)$ . Then, we define

\begin{align*} \textrm{Sel}(F,A)=\ker\!\left (H^1(G_F,A)\to \prod \frac{H^1(G_{F_v},A)}{H^1_f(G_{F_v},A)}\right ), \end{align*}

where the product runs through all places of $F$ . We will often write $H^1_{/f}(G_{F_v},A)$ for the quotient $\frac{H^1(G_{F_v},A)}{H^1_f(G_{F_v},A)}$ . In addition, we will need the modified Selmer group:

\begin{align*} \textrm{Sel}'(F,A)=\ker\!\left (H^1(G_F,A)\to \prod _{v\notin S} \frac{H^1(G_{F_v},A)}{H^1_f(G_{F_v},A)}\right ), \end{align*}

where $S$ is the set of all primes above $p$ . For any infinite algebraic extension $M$ of $K$ , we define

\begin{align*} \textrm{Sel}'(M,A)=\varinjlim _{{K\subset F\subset M}}\textrm{Sel}'(F,A), \quad \textrm{Sel}(M,A)=\varinjlim _{{K\subset F\subset M}}\textrm{Sel}(F,A). \end{align*}

Lemma 4.2. Let $K_c$ be the cyclotomic $\mathbb{Z}_p$ -extension of $K$ . Then there is an isomorphism of groups:

\begin{align*} \textrm{Sel}'(K_c,A)\cong \textrm{Sel}'(\mathcal{K},A)^{\textrm{Gal}(\mathcal{K}/K_c)}. \end{align*}

Proof. Consider the inflation restriction exact sequence:

\begin{align*} H^1(\textrm{Gal}(\mathcal{K}/K_c),A)\to H^1(G_{K_c},A)\to H^1(G_{\mathcal{K}},A)^{\textrm{Gal}(\mathcal{K}/K_c)}\to H^2(\textrm{Gal}(\mathcal{K}/K_c),A). \end{align*}

Note that $\textrm{Gal}(\mathcal{K}/K_c)\cong \mathbb{Z}_p\times \Delta$ and that the order of $\Delta$ is coprime to $p$ by assumption. Thus, to show that $H^i(\textrm{Gal}(\mathcal{K}/K_c),A)$ is trivial for $i=1,2$ , it suffices to consider $H^i(\Gamma, A)$ for the unique subgroup $\Gamma \subset \textrm{Gal}(\mathcal{K}/K_c)$ that is isomorphic to $\mathbb{Z}_p$ . Let $\tau$ be a topological generator of $\Gamma$ . Recall that

\begin{align*} \rho \colon G_{\mathbb{Q}}\to \mathcal{O}_\pi ^\times \end{align*}

is the representation given by the action of $G_{\mathbb{Q}}$ on $A$ . Note that $\rho (\tau )\neq 1$ by definition. In particular, $\rho (\tau )-1\in \mathcal{O}_\pi \setminus \{0\}$ . Let $\delta \colon \Gamma \to A$ be a cocycle. As $A$ is $\mathcal{O}_{\pi }$ -divisible, we can find an element $x\in A$ such that $(\rho (\tau )-1)x=\delta (\tau )$ . As a cocyle on $\Gamma$ is uniquely determined by the image of $\tau$ , we see that $\delta$ is indeed a coboundary and $H^1(\Gamma,A)$ vanishes. As $\Gamma$ has cohomological dimension one, $H^2(\Gamma,A)$ also vanishes. Hence, we obtain an isomorphism:

\begin{align*} \Omega \colon H^1(G_{K_c},A)\to H^1(G_{\mathcal{K}},A)^{\textrm{Gal}(\mathcal{K}/K_c)}, \end{align*}

which induces an injection:

\begin{align*} \Omega '\colon \textrm{Sel}'(K_c)\to \textrm{Sel}'(\mathcal{K},A)^{\textrm{Gal}(\mathcal{K}/K_c)}. \end{align*}

To show that $\Omega '$ is an isomorphism, it suffices that $\Omega ^{-1}(\textrm{Sel}'(\mathcal{K},A)^{\textrm{Gal}(\mathcal{K}/K_c)})$ lies inside $\textrm{Sel}'(K_c,A)$ .

Let $\mathfrak{p}$ be the unique prime above $p$ in $K$ (in the inert case $\mathfrak{p}=(p)$ ). Let $\mathfrak{f'}$ be the product of the prime to $p$ part of $\mathfrak{f}$ and $\mathfrak{p}$ (so we are eliminating higher powers of $\mathfrak{p}$ in $\mathfrak{f}$ ). By definition, $\textrm{Gal}(\mathcal{K}/K(\mathfrak{f}'))\cong \mathbb{Z}_p^2$ . Let $K(\mathfrak{f}')_c$ be the cyclotomic $\mathbb{Z}_p$ -extension of $K(\mathfrak{f}')$ . Note that $\mathcal{K}/K(\mathfrak{f}')_c$ is a $\mathbb{Z}_p$ -extension and therefore unramified outside $p$ . Let $v$ be a place coprime to $p$ in $K(\mathfrak{f}')_c$ and $v'$ a place above $v$ in $\mathcal{K}$ . We denote by $I_v$ the inertia subgroup in $G_{(K(\mathfrak{f}')_c)_v}$ and by $I_{v'}$ the inertia subgroup in $G_{\mathcal{K}_{v'}}$ . Note that the natural restriction $I_{v'}\to I_v$ is an isomorphism as $\mathcal{K}/K(\mathfrak{f}')_c$ is unramified at $v$ . Then, the natural restriction homomorphism:

\begin{align*} H^1(I_{v},A)\to H^1(I_{v'},A) \end{align*}

is injective. It now follows from Definition 4.1 that

\begin{align*} H^1_{/f}(G_{(K(\mathfrak{f}')_c)_v},A)\to H_{/f}^1(G_{\mathcal{K}_{v'}},A) \end{align*}

is injective. By assumption, $\textrm{Gal}(K(\mathfrak{f}')_c/K_c)$ is an abelian group whose order is coprime to $p$ . Let $w$ be a place below $v$ in $K_c$ and let $C=\textrm{Gal}((K(\mathfrak{f}')_c)_v/(K_c)_w)$ . So, $C$ is a finite abelian group of order coprime to $p$ . The inflation restriction exact sequence now implies that

\begin{align*} H^1_{\textrm{ur}}(G_{(K(\mathfrak{f}')_c)_v},V(1))^C=H^1_{\textrm{ur}}(G_{(K_c)_w},V(1)) \end{align*}

and

\begin{align*} H^1(G_{(K(\mathfrak{f}')_c)_v},Z)^C=H^1(G_{(K_c)_w},Z) \end{align*}

for $Z\in \{V(1),T(1),A\}$ . It follows that

(4.1) \begin{equation} H^1_f(G_{(K_c)_w},Z)=H^1_f(G_{(K(\mathfrak{f}')_c)_v},Z)^C \end{equation}

for $Z\in \{T(1),V(1)\}$ . From the fact that $C$ is a group of order coprime to $p$ , we obtain an exact sequence:

\begin{align*} 0\to H^1_f(G_{(K(\mathfrak{f}')_c)_v},T(1))^C\to H^1_f(G_{(K(\mathfrak{f}')_c)_v},V(1))^C\to H^1_f(G_{(K(\mathfrak{f}')_c)_v},A)^C\to 0. \end{align*}

Together with equation (4.1), this implies

\begin{align*} H^1_f(G_{(K_c)_w},A)=H^1_f(G_{(K(\mathfrak{f}')_c)_v},A)^C. \end{align*}

Thus,

\begin{align*} H^1_{/f}(G_{(K_c)_w},A)=H^1((G_{(K(\mathfrak{f}')_c)_v},A)^C/H^1((G_{(K(\mathfrak{f}')_c)_v},A)^C=H^1_{/f}((G_{(K(\mathfrak{f}')_c)_v},A)^C, \end{align*}

where we used again that $\vert C\vert$ is coprime to $p$ for the last equality. Combining this with our computations for $v$ and $v'$ , we obtain an injection:

\begin{align*} H^1_{/f}(G_{(K_c)_w},A)\to H_{/f}^1(G_{\mathcal{K}_{v'}},A). \end{align*}

It now follows from the definition of the modified Selmer group that the preimage of $\textrm{Sel}'(\mathcal{K},A)^{\textrm{Gal}(\mathcal{K}/K_c)}$ under $\Omega$ lies inside $\textrm{Sel}'(K_c,A)$ which is exactly what we need to show.

Let $\mathcal{M}$ be the maximal $p$ -abelian $p$ -ramified extension of $\mathcal{K}$ . Let $X=\textrm{Gal}(\mathcal{M}/\mathcal{K})$ . Note that the completed group ring $\mathbb{Z}_p[\![\textrm{Gal}(\mathcal{K}/K)]\!]$ acts naturally on $X$ .

Lemma 4.3. There is an isomorphism of $\mathbb{Z}_p[\![\textrm{Gal}(\mathcal{M}/K)]\!]$ -modules:

\begin{align*} \textrm{Sel}'(\mathcal{K},A)\cong \textrm{Hom}(X,A), \end{align*}

where $\textrm{Hom}(\cdot,\cdot )$ is the module of continuous homomorphisms.

Proof. By definition, the representation $\rho$ factors through $\textrm{Gal}(\mathcal{K}/\mathbb{Q})$ [7, page 256]. It follows that $\textrm{Sel}'(\mathcal{K},A)\subset \textrm{Hom}(G_{\mathcal{K}},A)$ . Let $v$ be a place of $\mathcal{K}$ not lying above $p$ . Let $\textrm{res}_v$ be the natural restriction:

\begin{align*} \textrm{res}_v\colon \textrm{Hom}(G_{\mathcal{K}},A)\to \textrm{Hom}(G_{\mathcal{K}_v},A). \end{align*}

Let $\delta \in \textrm{Sel}'(\mathcal{K},A)$ , then $\textrm{res}_v(\delta )\in H^1_{f}(G_{{\mathcal{K}}_v},A)$ . In particular, $\textrm{res}_v(\delta )$ is trivial on the inertia group $I_v\subset G_{\mathcal{K}_v}\hookrightarrow G_{\mathcal{K}}$ . This holds for all place $v$ of $\mathcal{K}$ that do not lie above $p$ . Therefore, $\delta$ is trivial on the smallest subgroup $Y$ containing $\cup _{(v,p)=1}I_v$ and can therefore be seen as a homomorphism on $X$ with values in $A$ . We obtain that

\begin{align*} \textrm{Sel}'(\mathcal{K},A)\subset \textrm{Hom}(X,A). \end{align*}

Let conversely $\delta \in \textrm{Hom}(X,A)$ . We want to show that $\delta$ is already an element in $\textrm{Sel}'(\mathcal{K},A)$ . As $X$ is a quotient of $G_{\mathcal{K}}$ , there is a natural injection:

\begin{align*} \iota \colon \textrm{Hom}(X,A)\hookrightarrow \textrm{Hom}(G_{\mathcal{K}},A). \end{align*}

Then $\textrm{res}_v\circ \iota (\delta )\in H^1_f(\mathcal{K}_v,A)$ for all places $v$ of $\mathcal{K}$ coprime to $p$ . It follows that $\iota (\delta )$ is an element of $\textrm{Sel}'(\mathcal{K},A)$ . As $\iota$ is injective, $\delta$ is indeed an element in $\textrm{Sel}'(\mathcal{K},A)$ .

For any $\mathbb{Z}_p[\![\textrm{Gal}(\mathcal{K}/K)]\!]$ -module $M$ , we define $M(\rho ^{-1})$ as the $\mathcal{O}_\pi [\![\textrm{Gal}(\mathcal{K}/K)]\!]$ -module that is isomorphic to $M\otimes \mathcal{O}_{\pi }$ as an abelian group and is equipped with a $\textrm{Gal}(\mathcal{K}/K)$ -action given by:

\begin{align*} \sigma. m=\rho ^{-1}(\sigma )(\sigma m). \end{align*}

We call $M(\rho ^{-1})$ the twist of $M$ by $\rho ^{-1}$ . If $L$ is a field such that $K\subset L\subset \mathcal{K}$ , we define

\begin{align*} M(\rho ^{-1})_L=M(\rho ^{-1})\otimes _{\mathbb{Z}_p[\![\textrm{Gal}(\mathcal{K}/K)]\!]}\mathbb{Z}_p[\![\textrm{Gal}(L/K)]\!]. \end{align*}

Lemma 4.4. There is an isomorphism of $\mathcal{O}_\pi [\![\textrm{Gal}(K_c/K)]\!]$ -modules:

\begin{align*} \textrm{Sel}'(K_c,A)\cong \textrm{Hom}_{\mathcal{O}}(X(\rho ^{-1})_{K_c},K_{\pi }/\mathcal{O}_{\pi }). \end{align*}

Proof. We apply the two proceeding lemmata:

\begin{align*} \textrm{Sel}'(K_c,A)\cong \textrm{Sel}'(\mathcal{K},A)^{\textrm{Gal}(\mathcal{K}/K_c)}\cong \textrm{Hom}(X,A)^{\textrm{Gal}(\mathcal{K}/K_c)}. \end{align*}

The claim follows by twisting the right term by $\rho ^{-1}$ .

In the end, we are not interested in the modified Selmer group $\textrm{Sel}'(K_c,A)$ , but in the classical Selmer group $\textrm{Sel}(K_c,A)$ . Recall that we assumed that there is a unique prime above $p$ in $K$ . Thus, there is a unique prime above $p$ in $K_c$ . By a slight abuse of notation, we write $K_{c,p}$ for the completion of $K_c$ at this unique prime. Even though there might be more than one prime above $p$ in $\mathcal{K}$ , we will fix such a prime $v_{\infty }$ and write $\mathcal{K}_p$ for the completion at this prime. Let $F$ be an arbitrary subfield of $\mathcal{K}$ and $v$ any prime of $F$ above $p$ . Let $U_v(F)$ be the principal local units in $F_v$ . We write $U_p(F)$ in the case that $v$ is the unique prime below $v_{\infty }$ and $U_p$ for the projective limit $\varprojlim _{{K\subset F\subset \mathcal{K}}}U_p(F)$ . We denote the product $\prod _{v\mid p}U_v(F)$ by $U(F)$ and by $U$ the limit $\varprojlim _{{K\subset F\subset \mathcal{K}}}U(F)$ . In the next step, we will relate the classical Selmer group to a quotient of $U$ .

To do so, note that the definition of the classical Selmer group and the modified Selmer group give us a natural exact sequence:

\begin{align*} 0\to \textrm{Sel}(K_c,A)\to \textrm{Sel}'(K_c,A)\to H^1(G_{K_{c,p}},A)/H^1_f(G_{K_{c,p}},A). \end{align*}

In the following lemma, we will analyze the right-most term in more detail.

Lemma 4.5. There is an isomorphism of $\mathcal{O}_\pi [\![\textrm{Gal}(K_c/K)]\!]$ -modules:

\begin{align*} H^1(G_{K_{c,p}},A)\cong \textrm{Hom}_{\mathcal{O}}(U(\rho ^{-1})_{K_c},K_{\pi }/\mathcal{O}_{\pi }). \end{align*}

Proof. Note that the decomposition group at every prime above $p$ in $\mathcal{K}$ has the form $\mathbb{Z}_p^2\times \Delta _p$ for a finite abelian group $\Delta _p$ of order coprime to $p$ . In particular, $\textrm{Gal}(\mathcal{K}_p/(K_c)_p)\cong \mathbb{Z}_p\times \Delta _p$ . Using the same argument as in the global case (see the first paragraph of the proof of Lemma 4.2), we obtain $H^i(\textrm{Gal}(\mathcal{K}_p/K_{c,p}),A)=0$ for $1\le i\le 2$ . Thus, there is an isomorphism $H^1(G_{K_{c,p}},A)\cong H^1(G_{\mathcal{K}_p},A)^{\textrm{Gal}(\mathcal{K}_{p}/K_{c,p})}$ . Since $G_{\mathcal{K}_p}$ acts trivially on $A$ ,

\begin{align*} H^1(G_{\mathcal{K}_p},A)\cong \textrm{Hom}(G_{\mathcal{K}_p},A). \end{align*}

Recall that, by assumption, $\rho$ is nontrivial on $\Delta _p$ . By local class field theory,

\begin{align*} \textrm{Hom}(G_{\mathcal{K}_p},A)^{\Delta _p}=\textrm{Hom}(U_p,A)^{\Delta _p} \end{align*}

(compare this with [10, Proof of Proposition 5.2]). For each of the finitely many primes lying above $p$ in $\mathcal{K}$ , we obtain a copy of $U_{p}$ in $U$ . It can be verified that $\textrm{Hom}(U,A)=\textrm{Hom}(U_{p},A)^{\vert \Delta/\Delta _{p}\vert }$ . The group $\textrm{Gal}(\mathcal{K}/K)$ is abelian, so all primes above $p$ have the same decomposition group. Let $\{g_1,\dots, g_s\}$ be a set of representatives for $\Delta/\Delta _p$ and assume that $g_1=1$ . Recall that we assumed that the class number of $K$ is 1. Thus, $\Delta$ acts transitively on the set of primes above $p$ in $\mathcal{K}$ . There is an isomorphism:

\begin{align*} U=\prod _{i=1}^sg_iU_p. \end{align*}

Thus, we obtain an isomorphism of $\mathbb{Z}_p[\Delta ]$ -modules:

\begin{align*} \textrm{Hom}(U,A)=\prod _{i=1}^s g_i\textrm{Hom}(U_p,A). \end{align*}

It now follows that

\begin{align*} \textrm{Hom}(U,A)^\Delta \cong \textrm{Hom}(U_{p},A)^{\Delta _{p}}. \end{align*}

Twisting $\textrm{Hom}(U,A)$ by $\rho ^{-1}$ and taking $\textrm{Gal}(\mathcal{K}/K_c)$ -invariants finishes the proof.

Let $\mathcal{V}\subset U(\rho ^{-1})_{K_c}$ be the subgroup corresponding to $H^1_f(K_{c,p},A)$ , that is, there is an isomorphism:

\begin{align*} H^1_f(G_{K_{c,p}},A)\cong \textrm{Hom}_{\mathcal{O}}(U(\rho ^{-1})_{K_c}/\mathcal{V},K_{\pi }/\mathcal{O}_{\pi }). \end{align*}

This gives

Lemma 4.6. There is an isomorphism of $\mathcal{O}_\pi [\![\textrm{Gal}(K_c/K)]\!]$ -modules:

\begin{align*} \textrm{Sel}(K_c,A)\cong \textrm{Hom}_{\mathcal{O}}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V}),K_{\pi }/\mathcal{O}_{\pi }), \end{align*}

where $\Phi$ is induced by the natural homomorphism given by class field theory in terms of ideles $\Phi \colon U\to X$ .

Proof. Consider the following commutative diagram

By Lemmas 4.4 and 4.5, the vertical maps are isomorphisms. It follows that

\begin{align*} \textrm{Sel}(K_c,A)&\cong \beta _1^{-1}(H^1_f(G_{K_{c,p}},A))\cong \beta _2^{-1}(\textrm{Hom}_{\mathcal{O}}(U(\rho ^{-1})_{K_c}/\mathcal{V},K_{\pi }/\mathcal{O}_{\pi }))\\[5pt] &\cong \textrm{Hom}_{\mathcal{O}}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V}),K_{\pi }/\mathcal{O}_{\pi }). \end{align*}

5. The Kato zeta-element and the Coleman map

In the previous section, we related the Selmer group we are interested in to the module $\textrm{Hom}_{\mathcal{O}}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V}),K_{\pi }/\mathcal{O}_{\pi })$ . In order to express its characteristic ideal in terms of a $p$ -adic $L$ -function, we will employ Kato’s theory of zeta-elements. To do so, note that every element $v\in V$ such that $v^{\pm }\neq 0$ (here $\pm$ stands for the projection to the $\pm 1$ eigenspaces of the complex conjugation of $V$ ) defines a lattice $T\subset V$ given by $T=\mathcal{O}_{\pi }v$ . We fix such a lattice once and for all.

Before we can state Kato’s main result, we have to introduce some further notation. Let $R$ be a ring that is contained in a finite extension of $\mathbb{Q}_p$ . Assume that $p$ is invertible in $R$ . We write $H^i(R,\cdot )$ for the étale cohomology group $H^i_{\textrm{et}}(\textrm{Spec}(R),\cdot )$ . Let $T$ be a $\mathbb{Z}_p$ -lattice with a continuous $G_{\mathbb{Q}}$ -action, then we define $H^i(R,T)=\varprojlim _{{n\in \mathbb{N}}}H^i(R,T/p^n)$ .

In our setting, $T$ will be the fixed Galois-invariant lattice $T\subset V$ and $R=\mathbb{Z}_p[\mu _{p^n},1/p]$ . To simplify notation, we write $H^1(T)$ for $\varprojlim _{{n\in \mathbb{N}}} H^i(\mathbb{Z}_p[\mu _{p^n},1/p],T)$ and $H^1(V)$ for $H^1(T)\otimes \mathbb{Q}_p$ . Note that $G_K$ acts naturally on $H^1(V)$ .

We have introduced the twist by the representation $\rho ^{-1}$ in the previous section. In what follows, we will frequently use Tate twists which are defined as follows: let $\kappa$ be the $p$ -cyclotomic character and $M$ a $G_{\mathbb{Q}}$ -module, then we denote by $M(l)$ the module $M(\kappa ^l)$ . Let $(\mu _{p^n})_n$ be a norm-coherent sequence of $p$ -power roots of unity. Then the multiplication with $(\mu _{p^n})_n^{\otimes (l)}$ induces an isomorphism $H^1(V)\to H^1(V(l))$ . If $z$ is an element in $H^1(V)$ , we denote its image in $H^1(V(l))$ by $z(l)$ (compare also with [7, page 221]).

Let $1\le r\le k-1$ be an integer. Each of the representations $V(r)$ is de Rham, meaning that $\dim _{\mathbb{Q}_p}((V(r)\otimes B_{\textrm{dr}})^{G_{\mathbb{Q}_p}})=2$ and the Hodge Tate weights are $(r,1-k+r)$ . Each de Rham module comes with a natural filtration $D^i_{\textrm{dr}}(V)$ induced by the filtration of $D_{\textrm{dr}}$ (see [2, Section 3]). Note that for $r$ chosen in the above range, the space $D^0(V(r))$ is one-dimensional and we fix a generator $\omega$ . There is a dual exponential map:

\begin{align*} \exp ^*_{V(r),n}\colon H^1(G_{\mathbb{Q}_p(\mu _{p^n})},V(r))\to D^0(V(r)). \end{align*}

Let $\textrm{per}\colon D^0(V(r))\to V$ be the period maps defined by Kato [7, page 162]. Then the choice of $v$ induces complex numbers $\Omega _\pm$ such that $\textrm{per}(\omega )=\Omega _+v^++\Omega _-v^-$ . From now on, we will denote by $G_n$ the group $\textrm{Gal}(\mathbb{Q}(\mu _{p^n})/\mathbb{Q})$ .

Definition 5.1. Kato assigns to every element $v\in V$ an element $z_v\in H^1(V)$ . We call the element assigned to our fixed choice of $v$ the Kato zeta-element and denote it by $z_{\textrm{kato}}$ .

Lemma 5.2. Let $\chi$ be a character of $G_n$ and let $\pm =\chi (\!-\!1)$ . Let $\theta ^\pm _\chi \colon \mathbb{Q}_p(\zeta _{p^n})\otimes \mathbb{Q}\to V^\pm$ be the map given by:

\begin{align*} x\otimes y\mapsto \sum _{\sigma \in G_n}\chi (\sigma )\sigma (x)\textrm{per}^\pm (y). \end{align*}

We have the following interpolation formula:

\begin{align*} \theta _\chi ^\pm \exp ^*_{V(k-1),n}(z_{\textrm{kato}}(k-1))=(2\pi i)^{k-2}\frac{1}{\Omega _{\pm }} L_{(p)}(f,\chi,1)v^{\pm }. \end{align*}

Proof. Immediate from [7, Lemma 12.5] for $r=k-1$ .

As $p$ is a potentially ordinary prime (and not ordinary) for $f$ , the representation $V$ is not crystalline. Instead of the crystalline part, we will study

\begin{align*} D_{\textrm{cycl}}(V)=\varinjlim _{{\mathbb{Q}_p\subset K'\subset \mathbb{Q}_p^{\textrm{cy}}}}(B\otimes B_{\textrm{crys}})^{G_{K'}}, \end{align*}

where $\mathbb{Q}_p^{\textrm{cy}}=\cup _n\mathbb{Q}_p(\mu _n)$ is the maximal cyclotomic extension of $\mathbb{Q}_p$ . Let $G^{cy}\cong \textrm{Gal}(\mathbb{Q}_p^{nr}/\mathbb{Q}_p)\times \mathbb{Z}_p^{\times }$ be the Galois group $\textrm{Gal}(\mathbb{Q}_p^{\textrm{cy}}/\mathbb{Q}_p)$ . Then $D_{\textrm{cycl}}(V)$ is a $(\varphi,G^{cy})$ -module [4, page 41 ff.]. Note that by definition, $D_{\textrm{cycl}}(V)$ is a two-dimensional vector space over the completion of the maximal unramified extension of $\mathbb{Q}_p$ .

Recall that we assume that $f$ has potentially ordinary reduction at $p$ and ordinary reduction over $\mathbb{Q}_p(\mu _p)$ . Thus, there is a one-dimensional $G_{\mathbb{Q}_p(\mu _p)}$ -subrepresentation $V'\subset V$ that is unramified.

Lemma 5.3. The subspace $V'$ is $G_{\mathbb{Q}_p}$ -stable and $\varphi$ acts as multiplication by an element $\alpha _1\in \mathbb{Z}_p^\times$ on $(B_{\textrm{crys}}\otimes V')^{G_{\mathbb{Q}_p(\mu _p)}}$ .

Proof. Let $V''=V/V'$ . Then $V''$ is ramified as $G_{\mathbb{Q}_p(\mu _p)}$ -representation. Let $I\subset G_{\mathbb{Q}_p(\mu _p)}$ be the inertia subgroup of $G_{\mathbb{Q}_p(\mu _p)}$ . Then, $V'$ is the unique subspace that is fixed by $I$ . As $I$ is a normal subgroup of $G_{\mathbb{Q}_p}$ it follows that $V'$ is stable under $G_{\mathbb{Q}_p}$ .

It remains to show that there is a $p$ -adic unit $\alpha _1$ such that $\varphi$ acts as $\alpha _1$ on $(B_{\textrm{crys}}\otimes V')^{G_{\mathbb{Q}_p(\mu _p)}}$ . As $V'$ is unramified, we see that $(B_{\textrm{crys}}\otimes V')^{G_{\mathbb{Q}_p(\mu _p)}}$ has slope zero. In particular, $\varphi$ has to act via multiplication by some $\alpha _1\in \overline{\mathbb{Q}_p}$ with trivial $p$ -valuation. It remains to show that $\alpha _1\in \mathbb{Q}_p$ . By definition, $\mathbb{Q}_p$ is the maximal unramified extension of $\mathbb{Q}_p$ in $\mathbb{Q}_p(\mu _p)$ . As $V$ is crystalline as $G_{\mathbb{Q}_p(\mu _p)}$ -representation, it follows that $(B_{\textrm{crys}}\otimes V)^{G_{\mathbb{Q}_p(\mu _p)}}$ is a $2$ -dimensional $\mathbb{Q}_p$ -vector space. Let $P(x)\in \mathbb{Q}_p[x]$ be the characteristic polynomial of the action of $\varphi$ on $(B_{\textrm{crys}}\otimes V)^{G_{\mathbb{Q}_p(\mu _p)}}$ . Clearly, $\alpha _1$ is a root of $P(x)$ . Let $\beta _1$ be the other root. As $V''$ is ramified, we see that $\beta _1$ cannot be a unit. Thus, $v_p(\alpha _1\beta _1)=v_p(\beta _1)\neq 0$ . If $\alpha _1\notin \mathbb{Q}_p$ , then $\alpha _1$ and $\beta _1$ are Galois conjugate. In particular, $\alpha _1$ and $\beta _1$ would have the same $p$ -adic valuation yielding a contradiction to the fact that $v_p(\alpha _1)=0$ .

The action of $G_{\mathbb{Q}_p}$ on $V'$ factors through $\textrm{Gal}(\mathbb{Q}_p^{\textrm{ur}}(\mu _p)/\mathbb{Q}_p)\cong \textrm{Gal}(\mathbb{Q}_p^{\textrm{ur}}/\mathbb{Q}_p)\times \textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ . Thus, the restriction to $\textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ is given by a character $\varepsilon$ . We can therefore find a character $\varepsilon$ of $\textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ such that $V'\otimes \varepsilon ^{-1}$ is an unramified representation of $G_{\mathbb{Q}_p}$ .

Let $f=\sum a_nq^n$ and let $\tilde{f}=\sum _n\tilde{a}_nq^n$ be the newform such that $\tilde{f}(\varepsilon )=f$ , where we denote by $\tilde{f}(\epsilon )$ the modular form such that $\tilde{a}_l(f)\varepsilon (l)=a_l(f)$ for $(l,p)=1$ . The modular form $\tilde{f}$ is not necessarily again a $CM$ -form. In fact, if $f$ is the modular form corresponding to a modular elliptic curve, then $\tilde{f}$ is not $CM$ and might not have good reduction at $p$ .

Let $F$ be the smallest extension of $\mathbb{Q}_p$ that contains all the coefficients of $\tilde{f}$ and let $V(\tilde{f})$ be the $2$ -dimensional $F$ -representation associated with $\tilde{f}$ . We have $V\otimes F=V(\tilde{f})\otimes \varepsilon$ as one can easily see from the computation of the traces and norms of the Frobenius automorphisms at the primes not dividing $pN$ . By definition, the representation $V(\tilde{f})$ is always semistable at $p$ .

Lemma 5.4. The representation $V(\tilde{f})$ has an unramified $G_{\mathbb{Q}_p}$ -subrepresentation $V'(\tilde{f})$ , the vector space $D_{\textrm{crys}}(V(\tilde{f}))$ is at least one-dimensional and there is a $p$ -adic unit $\alpha$ such that $\varphi$ acts via multiplication by $\alpha$ on $D_{\textrm{crys}}(V'(\tilde{f}))$ .

Proof. The first claim follows by setting $V'(\tilde{f})=V'\otimes \varepsilon ^{-1}$ . The second claim follows as $V'(\tilde{f})$ is crystalline as a representation over $G_{\mathbb{Q}_p}$ . Now we can conclude the existence of $\alpha$ as in Lemma 5.3.

Corollary 5.5. Let $\alpha$ be as in Lemma 5.4 and let $\alpha _1$ be as in Lemma 5.3 . Then, we have

\begin{align*} \alpha =\alpha _1. \end{align*}

Proof. Let $e'_0$ be an $\alpha _1$ -eigenvector of $\varphi$ in $(B_{\textrm{crys}}\otimes V')^{G_{\mathbb{Q}_p(\mu _p)}}$ . Then the group $\textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ acts via $\varepsilon$ on $e'_0$ . Let $e_0$ be the image of $e'_0$ in $(B_{\textrm{crys}}\otimes V'(\tilde{f}))^{G_{\mathbb{Q}_p(\mu _p)}}$ . Then $e_0$ is again an $\alpha _1$ -eigenvector of $\varphi$ . It is also fixed by $\textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ . So, $e_0$ is an element in $(B_{\textrm{crys}}\otimes V'(\tilde{f}))^{G_{\mathbb{Q}_p}}=D_{\textrm{crys}}(V'(\tilde{f}))$ . Thus, $\alpha =\alpha _1$ .

Recall that we have already fixed a Galois stable lattice $T\subset V$ . We choose the lattice $T(\tilde{f})$ such that $T(\tilde{f})\otimes \varepsilon \cong T$ .

Lemma 5.6. We have $F=\mathbb{Q}_p$ .

Proof. Let $\tilde{f}=\sum \tilde{a}_nq^n$ . Let $l$ be a prime coprime to $p$ . Then, $\tilde{a}_l\varepsilon (l)=a_l$ . As $\varepsilon$ takes values in the $(p-1)$ -th roots of unity and $a_l\in \mathbb{Q}_p$ , we see that $\tilde{a}_l\in \mathbb{Q}_p$ . It remains to consider the coefficient $\tilde{a}_p$ . Let $\psi$ be the nebentypus of $\tilde{f}$ , then $\psi \varepsilon ^2$ is the nebentypus of $f$ . By [7, page 271]:

\begin{align*} 1-\tilde{a}_pu +\psi (p)p^{k-1}u^2=\det (1-\varphi u\textrm{ on } D_{\textrm{crys}}(V(\tilde{f}))). \end{align*}

Note that $(1-\alpha u)$ divides this polynomial in $\mathbb{Q}_p$ . Further, $\psi (l)\varepsilon ^2(l)\in \mathbb{Q}_p$ for all $l$ coprime to $p$ . This implies that $\psi (p)\in \mathbb{Q}_p$ . Let

\begin{align*} 1-\tilde{a}_pu +\psi (p)p^{k-1}u^2=(1-\alpha u)(1-\beta u). \end{align*}

Note that $\beta =0$ if $p$ divides the conductor of $\psi$ . In both cases, we obtain $\beta \in \mathbb{Q}_p$ and it follows that $\tilde{a}_p=\alpha +\beta \in \mathbb{Q}_p$ . Thus, $\tilde{a}_p$ lies in $\mathbb{Q}_p$ .

Let $\widehat{\mathbb{Q}^{\textrm{ur}}_p}$ be the completion of the maximal unramified extension of $\mathbb{Q}_p$ . By definition, $D_{\textrm{cycl}}(V)=\widehat{\mathbb{Q}_p^{\textrm{ur}}}\otimes _{\mathbb{Q}_p} (B_{\textrm{crys}}\otimes V_F)^{G_{\mathbb{Q}_p(\mu _p)}}$ (see also [4, page 42]). For any de Rahm representation $W$ of $G_{\mathbb{Q}_p}$ , we denote by:

\begin{align*} [\cdot,\cdot ]\colon (B_{\textrm{dr}}\otimes W(k-1))^{G_{\mathbb{Q}_p(\mu _{p^n})}}\times D_{\textrm{cycl}}^{\mathbb{Q}_p(\mu _{p^n})}(W^*(1-k))\to \widehat{\mathbb{Q}_p^{\textrm{ur}}}(\mu _{p^n}) \end{align*}

the pairing defined by Delbourgo in [4, Definition 1.3].

Let $G_{\infty }=\textrm{Gal}(\mathbb{Q}_p(\mu _{p^\infty })/\mathbb{Q}_p)$ and $L$ be a finite extension of $\mathbb{Q}_p$ . Let $\Delta '$ be the torsion subgroup of $G_{\infty }$ , and let $\tau$ be a topological generator for the $\mathbb{Z}_p$ -free part. Let $T=\tau -1$ . We define

\begin{align*} \mathcal{H}_L[G_{\infty }]=\left \{ \sum _{\sigma \in \Delta '}\sigma h_{n,\sigma }T^n L[\Delta '][\![T]\!]\mid \lim _{n\to \infty }(\vert h_{n,\sigma }\vert _p/n^r)=0 \text{ for all } \sigma \text{ and some } r\gt 0\right \}. \end{align*}

If $L=\mathbb{Q}_p$ , we omit the subscript $L$ .

Let

\begin{align*} \textrm{EXP}\colon \varprojlim _{n\in \mathbb{N}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k))\otimes D_{\textrm{cycl}}(V^*(1-k))\to \mathcal{H}_{\mathbb{Q}_p(\mu _p)}[G_{\infty }] \end{align*}

be the exponential map defined by Delbourgo in [4, Theorem 1.4]. Note that the target is $\mathcal{H}_{\mathbb{Q}_p(\mu _p)}[G_{\infty }]$ as we assume that none of the eigenvectors of $\varphi$ on $D_{\textrm{cycl}}(V)$ is a power of $p$ .

Lemma 5.7. The image of $\textrm{EXP}$ lies inside $\mathcal{H}[G_{\infty }]$ .

Proof. This follows directly from Delbourgo’s construction: we assume that $f$ obtains good ordinary reduction over $\mathbb{Q}_p(\mu _p)$ . Thus, we can choose $n=0$ in Delbourgo’s construction (see [4, page 42]). Let now $\Psi$ be a character of $G_1=\textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ and define

\begin{align*} \mathcal{M}(T(k),\Psi )=\varprojlim _{{m\in \mathbb{N}}} H^1(G_{\mathbb{Q}_p(\mu _{p^m})},T(k))\otimes ((V^*(1-k)\otimes B_{\textrm{crys}}(\mu _p))^{\textrm{Gal}(\overline{\mathbb{Q}}_p/\mathbb{Q}_p(\mu _p)})^{G_1=\Psi }. \end{align*}

Delbourgo then constructs homomorphisms:

\begin{align*} \mathcal{EXP}_{\infty,\Psi }\colon \mathcal{M}(T(k),\Psi )\otimes \psi \to \mathcal{H}[G_{\infty }]. \end{align*}

Note that Delbourgo defines this map with image in $\mathcal{H}[G_{\infty }][T^{-1}]$ . The image lies again in the smaller ring $\mathcal{H}[G_{\infty }]$ by our assumption on the eigenvalues of $\varphi$ . Delbourgo then twists $\mathcal{EXP}_{\infty,\Psi }$ by a character of $\textrm{Gal}(\mathbb{Q}_p(\mu _p)/\mathbb{Q}_p)$ to obtain $\textrm{EXP}$ . But each such character has values in $\mathbb{Z}_p$ giving the desired claim.

Recall that $\kappa$ is the cyclotomic character on $G_{\infty }$ . Let $e_0$ be an $\alpha$ -eigenvector of $\varphi$ on $D_{\textrm{cycl}}(V^*(1-k))\cong D_{\textrm{cycl}}(V)$ (see Lemma 5.4 for the existence of $e_0$ ). We define the Coleman map:

\begin{align*} \mathcal{L}_{e_0}\colon \varprojlim _{{n\in \mathbb{N}}}H_{/f}^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))\to \mathcal{H}[G_{\infty }] \end{align*}

by $\kappa \circ EXP_{\infty }^*((x(1)) \otimes e_0)$ , where $x(1)$ denotes the image of $x$ under the isomorphism:

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))\to \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k)) \end{align*}

and $\kappa$ stands for the twist on $\mathcal{H}[G_{\infty }]$ given by $\gamma =\kappa (\gamma )\gamma$ . Note that we write $V(\epsilon )$ for the twist of a representation by a character $\epsilon$ and $\kappa \circ$ if we twist a homomorphism with image in $\mathcal{H}_L[G_{\infty }]$ , that is, if we compose such a homomorphism with $\kappa$ .

Delbourgo originally constructs $\mathcal{L}_{e_0}$ as a homomorphism on the projective limit:

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1)). \end{align*}

But it is immediate from the interpolating property and the fact that the module $H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))$ lies in the kernel of the dual exponential map, that $\mathcal{L}_{e_0}$ factors through $H^1_{/f}(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))$ .

Lemma 5.8. Let $z$ be an element in $\varprojlim _{{n\in \mathbb{N}}}H^1_{/f}(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))$ and $\chi$ be a character of conductor $p^n\ge p^2$ . Then,

\begin{align*} \chi \mathcal{L}_{e_0}(z)=\sum _{\tau \in G_n}\chi \varepsilon ^{-1}(\iota \tau )\mu ^{\tau }_{p^n}\alpha ^{-n}[\sum _{\sigma \in G_n}\chi ^{-1}(\sigma )\exp ^*_{V(k-1),n}(z_n)^{\sigma }, e_0]. \end{align*}

Proof. This is immediate from [4, Theorem 1.4], the action of $G_n=\textrm{Gal}(\mathbb{Q}_p(\mu _{p^n})/\mathbb{Q}_p)$ on $e_0$ and the fact that $\alpha _1=\alpha$ .

Recall that $\tilde{f}$ has a nontrivial Euler factor at $p$ . So, we can use the constructions of Perrin-Riou to define a second Coleman map as follows:

Let $\eta \in D_{\textrm{crys}}(V(\tilde{f})^*(1-k))$ be an eigenvector of $\alpha$ (see [7, Theorem 16.6] for its existence). According to [7, Theorem 16.4], there is a Coleman map:

\begin{align*} \mathcal{L}_{\eta }\colon \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k))\to \mathcal{H}[G_{\infty }] \end{align*}

such that

(5.1) \begin{equation} \mathcal{L}_{\eta }(x)(\kappa \chi ^{-1})=G(\chi,\mu _{p^n})^{-1}\sum _{\sigma \in G_n}\chi (\sigma )[(\textrm{exp}^*_{V(\tilde{f})(k-1),n}(x(\!-\!1)_n)^\sigma,((p^{-1}\varphi )^{-n}(\eta )], \end{equation}

where $G(\chi,\mu _{p^n})$ is a Gauss-sum. Here, $\exp ^*_{V(\tilde{f})(k-1),n}$ denotes the dual exponential map with respect to the representation $V(\tilde{f})(k-1)$ (see also page 21) and $x(\!-\!1)_n$ is the image of $x$ under

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k))\to \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k-1)) \end{align*}

\begin{align*} \to H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k-1)), \end{align*}

which is induced by the Tate twist as defined at the beginning of the present section. Note that $\mathcal{L}_\eta$ can be seen as a homomorphism defined on the quotient:

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k))/\varprojlim _{{n\in \mathbb{N}}}H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k-1)) (1). \end{align*}

The equality $V=V(\tilde{f})\otimes \varepsilon$ induces an isomorphism $V(\tilde{f})(k)\otimes \varepsilon =V(k)$ as follows: let $\mathbb{Q}_pe$ be a one-dimensional vector space on which $G_{\mathbb{Q}}$ acts via $\varepsilon ^{-1}$ , that is, $\sigma (e)=\varepsilon ^{-1}(\sigma )e$ . Then $v\mapsto v\otimes e$ defines a linear map $V(\tilde{f})(k)\to V(k)$ . By the choice of the lattice $T(\tilde{f})$ and the definition of Tate twists, we obtain homomorphisms (of $\mathbb{Z}_p$ -modules):

\begin{align*} \beta _1\colon \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))\to \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k)) \end{align*}

and

\begin{align*} \beta _2\colon \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k))\to \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k)). \end{align*}

We write $\beta =\beta _2\circ \beta _1$ . The following lemma relates the Coleman maps $\mathcal{L}_{e_0}$ and $\mathcal{L}_{\eta }$ .

Lemma 5.9. The eigenvector $e_0$ can be chosen such that the following equality holds for every character $\chi$ of conductor at least $p^2$ and every element $z$ in $\varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))$ :

\begin{align*} \chi \varepsilon ^{-1}\kappa \mathcal{L}_{\eta }(\beta (z)) =\chi (\mathcal{L}_{e_0}(z)). \end{align*}

The twist by $\kappa$ occurs on the left-hand side as a twist by $\kappa$ is already part of the definition of $\mathcal{L}_{e_0}$ .

Proof. Note that $\frac{p^n}{G(\chi ^{-1},\mu _{p^n})}=\sum _{\sigma \in G_n}\chi (\iota \sigma )\mu _{p^n}^\sigma$ . There is a series of injective $\mathbb{Z}_p$ -homorphisms:

\begin{align*} D_{\textrm{crys}}(V(\tilde{f})^*(1-k))\otimes \widehat{\mathbb{Q}_p^{ur}}\subset D_{\textrm{cycl}}(V(\tilde{f})^*(1-k))\to D_{\textrm{cycl}}(V^*(1-k)). \end{align*}

The $\alpha$ -eigenspace of $D_{\textrm{crys}}(V(\tilde{f})^*(1-k))$ is one-dimensional. We choose $e_0$ as the image of $\eta$ under these maps. Let $x\in H^1(\mathbb{Q}_p(\mu _{p^n}),V(\tilde{f})(k-1))$ and $x'$ its image in $H^1(\mathbb{Q}_p(\mu _{p^n}),V(k-1))$ . The $G_n$ -equivariance of $[\cdot,\cdot ]$ implies

\begin{align*} [\!\exp ^*_{V(\tilde{f})(k-1),n}x,\eta ]=[\!\exp ^*_{V(k-1),n}x',e_0]. \end{align*}

Note that $(x^\sigma )'=\varepsilon ^{-1}(\sigma )(x')^\sigma$ . Let $x=\beta (z)(\!-\!1)$ and $x'=z$ . Now,

\begin{align*} \chi \varepsilon ^{-1}\kappa \mathcal{L}_{\eta }(\beta (z)) =\chi (\mathcal{L}_{e_0}(z)) \end{align*}

follows from Lemma 5.8 and (5.1).

The following lemmata are a preparation to show that the kernel and cokernel of $\mathcal{L}_{e_0}$ are finite.

Lemma 5.10. Let $T'(\tilde{f})=T(\tilde{f})\cap V'(\tilde{f})$ . The following inclusion holds

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k-1))\subset \varprojlim _{{n\in \mathbb{N}}}H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k-1)). \end{align*}

Proof. Note that $H^0(G_{\mathbb{Q}_p(\mu _{p^n})},V'(\tilde{f})(k-1))=H^0(G_{\mathbb{Q}_p(\mu _{p^n})},V(\tilde{f})(k-1))=\{0\}$ . It follows from [2, Corollary 3.8.4] that

\begin{align*} &\dim _{\mathbb{Q}_p}(H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},V'(\tilde{f})(k-1))\\[5pt] &\quad=\dim _{\mathbb{Q}_p}((B_{\textrm{dr}}\otimes V'(\tilde{f})(k-1))^{G_{\mathbb{Q}_p(\mu _{p^n})}}/(B_{\textrm{dr}}^+\otimes V'(\tilde{f})(k-1))^{G_{\mathbb{Q}_p(\mu _{p^n})}})\\[5pt] &\quad=p^{n-1}(p-1)\\[5pt] &\quad=\dim _{\mathbb{Q}_p}(H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},V(\tilde{f})(k-1)). \end{align*}

We obtain

\begin{align*} H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},V(\tilde{f})(k-1))=H^1(G_{\mathbb{Q}_p(\mu _{p^n})},V'(\tilde{f})(k-1)). \end{align*}

Therefore,

\begin{align*} H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k-1))\subset H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k-1)). \end{align*}

Taking projective limits implies the claim.

Lemma 5.11. Let $V''(\tilde{f})=V(\tilde{f})/V'(\tilde{f})$ . Let $T'(\tilde{f})=T(\tilde{f})\cap V'(\tilde{f})$ and $T''(\tilde{f})=T(\tilde{f})/T'(\tilde{f})$ . The eigenvector $\eta \in D_{\textrm{crys}}(V''(k-1)^*)$ can be chosen such that $\mathcal{L}_{\eta }$ induces an injection:

\begin{align*} \mathcal{L}_{\eta }\colon \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f}^*)(k))/\varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k))\to \mathbb{Z}_p[\![G_{\infty }]\!] \end{align*}

with finite cokernel.

Proof. If $\tilde{f}$ has good ordinary reduction at $p$ , this is [7, Proposition 17.11]. It remains the case that $\tilde{f}$ does not have good ordinary reduction at $p$ . We will first show that $\varprojlim _{{n\in \mathbb{N}}}H^2(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k))$ is finite. By [7, page 233] the Pontryagin dual of $\varprojlim _{{n\in \mathbb{N}}}H^2(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k))$ is isomorphic to

\begin{align*} H^0(G_{\mathbb{Q}_p(\mu _{p^\infty })},\textrm{Hom}_{\mathbb{Z}_p}(T'(\tilde{f}),\mathbb{Q}_p/\mathbb{Z}_p)(1)). \end{align*}

This group can only be infinite if $V'(\tilde{f})$ has a nontrivial subrepresentation that factors through $G_{\infty }$ . As $V'(\tilde{f})$ is unramified this is impossible. Therefore, the module $\varprojlim _{{n\in \mathbb{N}}}H^2(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k))$ is finite. Applying group cohomology to the tautological exact sequence:

\begin{align*} 0\to T'(\tilde{f})(k)\to T(\tilde{f}(K))\to T''(\tilde{f})(k)\to 0, \end{align*}

yields that

\begin{align*} \delta &:\varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k))/\varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T'(\tilde{f})(k))\\[5pt] &\to \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T''(\tilde{f})(k)) \end{align*}

is injective with finite cokernel.

By Lemma 5.10, the homomorphism $\mathcal{L}_{\eta }$ factors through $\delta$ for every possible choice of $\eta$ . So we are left to show that we can choose $\eta$ such that $\mathcal{L}_\eta$ is induced by an injective homomorphism:

\begin{align*} \mathcal{L}'_{\eta }\colon \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T''(\tilde{f})(k))\to \mathbb{Z}_p[\![G_{\infty }]\!] \end{align*}

with finite cokernel. As $V'(\tilde{f})$ is unramified the same holds for $V''(\tilde{f})(k-1)$ . Further, $H^0(G_{\mathbb{Q}_p}, T''(\tilde{f})$ $(k-1))=\{0\}$ . Thus, we can apply [7, Lemma 17.12] to obtain the result.

Lemma 5.12. Let $\eta$ be chosen as in Lemma 5.11 . Then, $\varphi (\eta )=\alpha \eta$ .

Proof. By construction, $\eta \in D_{\textrm{crys}}((V''(\tilde{f})(k-1))^*)$ . Note that $(V(\tilde{f})(k-1))^*$ is isomorphic to $V(\tilde{f})$ . To conclude that $\varphi (\eta )=\alpha \eta$ , it suffices to show that $\varphi$ acts as the multiplication by a $p$ -adic unit on $\eta$ . As $V''(\tilde{f})(k-1)$ is unramified, the same holds for $(V''(\tilde{f})(k-1))^*$ . Thus, the eigenvalue of $\varphi$ on $D_{\textrm{crys}}(V''(\tilde{f})^*(1-k))$ is a $p$ -adic unit proving the lemma.

For the rest of the article, we fix $\eta$ as in the assumptions of Lemma 5.11. Let $v'$ be the generator of $T(\tilde{f})(k-1)$ given by our fixed choice of $v\in T$ . It follows from the choice of $\eta$ in the proof of [7, Lemma 17.12] that we can assume $[v',\eta ]=1$ .

Corollary 5.13. The homomorphism

\begin{align*} \mathcal{L}_{\eta }\colon \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f}^*)(k))/\varprojlim _{{n\in \mathbb{N}}}H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f}^*)(k-1))(1)\to \mathbb{Z}_p[\![G_{\infty }]\!] \end{align*}

is injective with finite cokernel.

Proof. This is a direct consequence of Lemmas 5.11 and 5.10.

Corollary 5.14. Let $e_0$ be the element corresponding to $\eta$ as in Lemma 5.9 . Then $\mathcal{L}_{e_0}$ is injective, the image lies in $\mathbb{Z}_p[\![G_{\infty }]\!]$ and the cokernel is finite.

Proof. By Lemma 5.9,

\begin{align*} \chi (\mathcal{L}_{e_0}(z))=\chi \varepsilon ^{-1}\kappa \mathcal{L}_{\eta }(\beta (z)). \end{align*}

As an element in $\mathcal{H}[G_{\infty }]$ is uniquely defined via its interpolation property,

\begin{align*} \kappa \varepsilon ^{-1}\circ \mathcal{L}_{\eta }(\beta (z))=\mathcal{L}_{e_0}(z). \end{align*}

We will first show that the image of $\mathcal{L}_{e_0}$ lies inside $\mathbb{Z}_p[\![G_{\infty }]\!]$ . As $\kappa$ and $\varepsilon$ are characters with values in $\mathbb{Z}_p^\times$ , it suffices to show that $\mathcal{L}_{\eta }(\beta (z))\in \mathbb{Z}_p[\![G_{\infty }]\!]$ , which follows from Corollary 5.13.

An element $z$ lies in the kernel of $\mathcal{L}_{e_0}$ if and only if $\chi \mathcal{L}_{e_0}(z)=0$ for every character of conductor $p^n\ge p^2$ . Note that the twist by $\kappa \varepsilon ^{-1}$ induces a bijection on $\mathbb{Z}_p[\![G_{\infty }]\!]$ . Thus, if $z$ lies in the kernel of $\mathcal{L}_{e_0}$ , then $\mathcal{L}_\eta (\beta (z))=0$ . But $\mathcal{L}_{\eta }$ is injective as a homomorphism on

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k))/\varprojlim _{{n\in \mathbb{N}}}H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},T(\tilde{f})(k-1))(1) \end{align*}

by Corollary 5.13. As $\beta$ is bijective, $\mathcal{L}_{e_0}$ is injective.

It remains to show that $\mathcal{L}_{e_0}$ has finite cokernel. Using again that $\kappa \varepsilon$ induces a bijection on $\mathbb{Z}_p[\![G_{\infty }]\!]$ , it suffices again to see that $\mathcal{L}_\eta$ has finite cokernel. But this is again Corollary 5.13.

5.1. $p$ -adic $L$ -functions

We can define the $p$ -adic $L$ -function for $\tilde{f}$ as in [7, Theorem 16.2].

Definition 5.15. Let $L_p(\tilde{f})$ be the element in $\mathcal{H}[G_{\infty }]$ constructed in [ 7, Theorem 16.2]. The $p$ -adic $L$ -function $L_p(\tilde{f})$ has the following interpolating property:

\begin{align*} L_p(\tilde{f})(\kappa \chi ^{-1})=p^n\alpha ^{-n}G(\chi,\mu _{p^n})^{-1} (2\pi i)^{k-2}\frac{1}{\Omega _{\pm }}L_{(p)}(\tilde{f},\chi, r), \end{align*}

where the subscript $p$ on the right-hand side means that we omit the Euler factor at $p$ .

We can only define this $L$ -function for the twisted modular form $\tilde{f}$ as $f$ has a trivial Euler factor at $p$ .

To define a $p$ -adic $L$ -function for our original form $f$ , we twist by the character $\varepsilon ^{-1}\kappa$ .

Definition 5.16. Let $L_p(f)=\varepsilon ^{-1}\kappa \circ L_p(\tilde{f})$ be the $p$ -adic $L$ -function associated with $f$ .

By definition,

\begin{align*} \chi ^{-1} L_p(f)=\chi ^{-1}\kappa \varepsilon ^{-1}L_p(\tilde{f}). \end{align*}

The twist by $\kappa$ occurs in the definition of $L_p(f)$ because we want to show later that the Kato zeta-element gets mapped to $L_{(p)}(f)$ under $\mathcal{L}_{e_0}$ . As the definition of $\mathcal{L}_{e_0}$ contains already a twist by $\kappa$ , we have to add this twist also to the $p$ -adic $L$ -function.

The $p$ -adic $L$ -function $L_p(f)$ interpolates the values $L(f,\chi,1)$ in the following sense.

Lemma 5.17. Let $\chi$ be a character of conductor $p^n\ge p^2$ , then

\begin{align*} \chi ^{-1} L_{p}(f)=p^n\alpha ^{-n}G(\chi \varepsilon,\mu _{p^n})^{-1}(2\pi i)^{k-2}\frac{1}{\Omega _{\pm }}L_{(p)}(f,\chi,1). \end{align*}

Proof. By definition,

\begin{align*} \chi ^{-1} L_p(f)=p^n\alpha ^{-n}G(\chi \varepsilon,\mu _{p^n})^{-1}(2\pi i)^{k-2}\frac{1}{\Omega _{\pm }}L_{(p)}(\tilde{f},\chi \varepsilon,1). \end{align*}

Let $\psi$ be the nebentypus of $\tilde{f}$ . Then $f$ has nebentypus $\psi \varepsilon ^2$ . For every prime $l$ coprime to $p$

\begin{align*} (1-a_l(\tilde{f})\varepsilon (l)\chi (l)l^{-s}+\psi (l)\varepsilon ^2(l)\chi ^2(l)l^{k-1-2s})=(1-a_l(f)\chi (l)l^{-s}+(\psi \varepsilon ^2)(l)\chi ^{2}(l)l^{k-1-2s}). \end{align*}

So indeed, $L_p(f)$ interpolates the truncated $L$ -function $L_{(p)}(f,\chi,1)$ .

We close this section by the following important lemma.

Lemma 5.18. The following equation holds

\begin{align*} \mathcal{L}_{e_0}(z_{\textrm{kato}}(k-1))=L_p(f). \end{align*}

In particular, $L_p(f)$ is an element in $\mathbb{Z}_p[\![G_{\infty }]\!]$ .

Proof. Let $\chi$ be a character of $G_n$ , let $\pm =\chi (\!-\!1)$ and conductor at least $p^2$ . By Lemma 5.8,

\begin{align*} \chi \mathcal{L}_{e_0}(z_{\textrm{kato}}(k-1))&=\sum _{\tau \in G_n}\chi \varepsilon ^{-1}(\iota \tau )\mu ^{\tau }_{p^n}\alpha ^{-n}[\sum _{\sigma \in G_n}\chi ^{-1}(\sigma )\exp ^*_{V_F(k-1),n}(z_n)^{\sigma }, e_0]. \end{align*}

Now Lemma 5.2 implies by the arguments of the first paragraph of [7, page 272]

\begin{align*} &\sum _{\tau \in G_n}\chi \varepsilon ^{-1}(\iota \tau )\mu ^{\tau }_{p^n}\alpha ^{-n}[\sum _{\sigma \in G_n}\chi ^{-1}(\sigma )\exp ^*_{V(k-1),n}(z_n)^{\sigma }, e_0]\\[5pt] &\quad=\sum _{\tau \in G_n}\chi \varepsilon ^{-1}(\iota \tau )\mu ^{\tau }_{p^n}\alpha ^{-n}(2\pi i)^{k-2}\frac{1}{\Omega _{\pm }} L(f,\chi,1)\\[5pt] &\quad=\chi L_p(f), \end{align*}

where the last equality is due to Lemma 5.17. As this holds for all $\chi$ of conductor at least $p^2$ ,

\begin{align*} \mathcal{L}_{e_0}(z_{\textrm{kato}}(k-1))=L_p(f). \end{align*}

By Corollary 5.14, the image of $\mathcal{L}_{e_0}$ lies inside $\mathbb{Z}_p[\![G_{\infty }]\!]$ . Thus, $L_p(f)$ has to be an element in $\mathbb{Z}_p[\![G_{\infty }]\!]$ .

We are now in the position to define the $p$ -adic $L$ -function over the cyclotomic $\mathbb{Z}_p$ -extension of $\mathbb{Q}_p$ . Note that this is the $p$ -aqdic $L$ -function appearing in Theorem 1.2.

Definition 5.19. Recall that $\Delta '$ denotes the torsion subgroup of $G_{\infty }$ . Let $N$ be the norm of $\Delta '$ . Then, we define $L_p(f,\mathbb{Q})=NL_p(f)$ .

6. Properties of $\mathcal{V}$

In order to analyze the structure of the quotient $U(\rho ^{-1})_{K_c}/\mathcal{V}$ more closely, we make use of Rubin’s classical main conjecture. We denote the Iwasawa algebra with coefficients in $\mathbb{Z}_p$ associated with $\textrm{Gal}(\mathcal{K}/K)$ by $\Lambda _{\mathcal{K}}$ , that is, $\Lambda _{\mathcal{K}}=\mathbb{Z}_p[\![\textrm{Gal}(\mathcal{K}/K)]\!]$ . Recall that $\Delta '$ is the torsion subgroup of $G_{\infty }$ and that $\Lambda =\mathbb{Z}_p[\![T]\!]$ is the Iwasawa algebra associated with $\textrm{Gal}(\mathbb{Q}_c/\mathbb{Q})\cong \textrm{Gal}(K_c/K)$ . There is the following chain of isomorphisms:

\begin{align*} U(\rho ^{-1})_{K_{c}}/\mathcal{V}&\cong \textrm{Hom}_{\mathcal{O}}(H^1_f(G_{K_{c,p}},A),K_{\pi }/\mathcal{O}_{\pi })\\[5pt] &\cong \textrm{Hom}(H^1_f(G_{\mathbb{Q}_{c,p}},A),\mathbb{Q}_p/\mathbb{Z}_p)\otimes \mathcal{O}_{\pi }\\[5pt] &\cong \varprojlim _{{n\in \mathbb{N}}}\textrm{Hom}(H^1_f(G_{\mathbb{Q}_p(\mu _{p^n})},A),\mathbb{Q}_p/\mathbb{Z}_p)^{\Delta '}\otimes \mathcal{O}_{\pi }\\[5pt] &\cong \varprojlim _{{n\in \mathbb{N}}}H^1_{/f}(G_{\mathbb{Q}_p(\mu _{p^n})},T(k-1))^{\Delta '}\otimes \mathcal{O}_{\pi }, \end{align*}

where the first and the third isomorphism follow directly from the definition of $\mathcal{V}$ and the definition of group cohomology for infinite extensions over $\mathbb{Q}_p$ . The second isomorphism can be deduced as in [13, proof of Theorem 7.2] and the last one follows from Tate duality.

Lemma 6.1. The quotient $U(\rho ^{-1})_{K_{c}}/\mathcal{V}$ is pseudo-isomorphic to $\Lambda \otimes \mathcal{O}_{\pi }$ . Furthermore, $\mathcal{V}$ is pseudo-isomorphic to $\Lambda \otimes \mathcal{O}_{\pi }$ .

Proof. Using the above chain of isomorphisms, it suffices to consider the module:

\begin{align*} \varprojlim _{{n\in \mathbb{N}}}H^1_{/f}(\mathbb{Q}_p(\mu _{p^n}),T(k-1))^{\Delta '}. \end{align*}

By Corollary 5.14, the module $\varprojlim _{{n\in \mathbb{N}}}H^1_{/f}(\mathbb{Q}_p(\mu _{p^n}),T(k-1))^{\Delta '}$  embeds into the group ring $\mathbb{Z}_p[\![G_{\infty }]\!]^{\Delta '}\cong \Lambda$ via $\mathcal{L}_{e_0}$ with finite cokernel. Therefore, $U(\rho ^{-1})_{K_{c}}/\mathcal{V}$ has rank one and does not contain a torsion submodule. Thus, the first claim follows.

Recall that by assumption $\rho$ restricted to $\Delta _p$ is neither the inverse of the Teichmüller character nor the trivial character. Then [11, Theorem 5.1] implies that $U(\rho ^{-1})_{K_c}$ is free of $\Lambda \otimes \mathcal{O}_{\pi }$ -rank two. As $U(\rho ^{-1})_{K_{c}}/\mathcal{V}$ has rank one, the second claim follows.

For every submodule $M$ of $U(\rho ^{-1})_{K_{\infty }}$ , we let $M_{K_c}$ denote the image of $M$ in $U(\rho ^{-1})_{K_c}$ . Let $C$ be the group of elliptic units as defined in [11, Section 1]. Clearly, $C(\rho ^{-1})_{K_c}$ is a submodule of $U(\rho ^{-1})_{K_c}$ . Hence, it is torsion-free and of $\Lambda \otimes \mathcal{O}_\pi$ -rank one. By [11, Theorem 7.7], $C(\rho ^{-1})_{K_c}$ is free of rank one. We will denote a fixed generator by $\xi$ . For every ideal $\mathfrak{f}$ such that $\mathcal{O}^\times \to (\mathcal{O}/\mathfrak{f})^\times$ is injective and any integral ideal $\mathfrak{a}$ that is coprime to $6\mathfrak{f}$ Kato gives the definition of a compatible system of elements ${_{\mathfrak{a}}z}_{\mathfrak{f}p^n}$ in $K(\mathfrak{f}p^n)^\times$ . As long as $\mathfrak{f}p^n$ has at least two different prime factors, these elements are units and generate a submodule in $U$ that actually coincides with the elliptic units defined by Rubin. Kato also defines in [7, Section 15] an element $z_{\mathfrak{f}p^\infty }$ that might only exist in $\varprojlim _{{K\subset K'\subset \mathcal{K}}}H^1(\mathcal{O}(K')[1/p]^\times \otimes \mathbb{Z}_p\otimes Q(\mathbb{Z}_p[\![\textrm{Gal}(\mathcal{K}/K)]\!])$ , where $Q(\cdot )$ denotes the quotient field of the corresponding ring. Note that the quotient field only is necessary for the case that $\mathfrak{fp}$ has only one prime factor. In any case, multiplication with the augmentation ideal pushes the element $z_{\mathfrak{f}p^\infty }$ to an integral element. As $\rho$ restricted to $\Delta$ is neither the inverse of the Teichmüller character nor the trivial character, we can deduce that the image of $z_{\mathfrak{f}p^\infty }$ defines a submodule in $U(\rho ^{-1})_{K_c}$ that coincides with $C(\rho ^{-1})_{K_c}$ .

There is a natural homomorphism:

\begin{align*} \Psi \colon C(\rho ^{-1})_{K_c}\to U(\rho ^{-1})_{K_c}/\mathcal{V}. \end{align*}

Lemma 6.2. The homomorphism $\Psi$ defined above is injective.

Proof. By Lemma 6.1, the quotient $U(\rho ^{-1})_{K_c}/\mathcal{V}$ is pseudo-isomorphic to $\Lambda \otimes \mathcal{O}_{\pi }$ . Hence, $\Psi$ is either injective or has finite image. So, to show that $\Psi$ is injective it suffices to show the following lemma (Lemma 6.3).

Lemma 6.3. The element $\xi ^{p^l}$ does not lie in $\mathcal{V}$ for any choice of $l\ge 1$ .

Proof. The element $z_{p^{\infty }\mathfrak{f}}$ has a well-defined image in $H^1(V(k-1)\otimes K_{\pi })$ . To prove the lemma, it therefore suffices to show that $\mathcal{L}_{e_0}(z_{p^\infty \mathfrak{f}}(k-1))^{\Delta '}$ 4 is nontrivial.

By [7, Theorem 15.12], we know that the image of $z_{p^{\infty }\mathfrak{f}}$ in the cohomology group $H^1(G_{\mathbb{Q}(\mu _{p^n})},(V\otimes K_{\pi })(1))$ (after tensoring with our fixed $v$ ) gets mapped to $L_{(p)}(f,\chi, k-1)v^{\chi (-1)}$ under the map $\sum _{\sigma \in \textrm{Gal}(\mathbb{Q}(\mu _{p^n})/\mathbb{Q})}\chi (\sigma )\textrm{per}_f\circ \sigma \circ \exp _{V(1),n}^*$ . By applying [7, Theorem 12.5] for $r=k-1$ , this image coincides with the image of Kato’s zeta-element $z_{\textrm{kato}}(1)$ . Using the fact that $H^1(V)$ is a free $\Lambda \otimes \mathbb{Q}_p$ -module [7, Theorem 12.4 (2)], one can identify the image of Kato’s zeta-element in $H^1_{/f}(\mathbb{Q}_p(\mu _{p^n}),(T\otimes \mathcal{O}_{\pi })(1))$ with the image of $z_{p^\infty \mathfrak{f}}$ . The claim follows now—after taking the $k{-}2$ -th Tate twist—from Lemma 5.18.

Let $K_{\infty }$ be the unique $\mathbb{Z}_p^2$ -extension of $K$ . Let $Z\in \mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ be a prime element coprime to

\begin{align*} \textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V})) \end{align*}

and

\begin{align*} \textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(U(\rho ^{-1})_{K_c}/(\mathcal{V}+C(\rho ^{-1})_{K_c}). \end{align*}

Let $u\in U(\rho ^{-1})_{K_{\infty }}$ be such that the restriction of $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]u$ to $U(\rho ^{-1})_{K_c}$ is a submodule of $\mathcal{V}$ that contains $Z^a\mathcal{V}$ for some integer $a$ (such an element exists by Lemma 6.1). Then, $\tilde{\mathcal{V}}=(\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!])u$ is free of rank one over $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ .

Lemma 6.4. The following equality holds

\begin{align*} E(\rho ^{-1})_{K_{\infty }}\cap \tilde{\mathcal{V}}=\{0\}. \end{align*}

Proof. By [11, Corollary 7.8], the module $E(\rho ^{-1})_{K_{\infty }}$ is of rank one over the algebra $\mathcal{O}_{\pi }[\![\textrm{Gal}(K_{\infty }/K)]\!]$ and does not contain a torsion submodule. Choose topological generators $\tau$ and $\gamma$ of $\textrm{Gal}(K_{\infty }/K)$ such that $K_c$ is the fixed field of the subgroup generated by $\gamma$ . Let $T=\tau -1$ and $S=\gamma -1$ .

If $E(\rho ^{-1})_{K_{\infty }}\cap \tilde{\mathcal{V}}$ is nontrivial, the intersection with $C(\rho ^{-1})_{K_{\infty }}$ is nontrivial. As $\Psi$ is injective by Lemma 6.2, this intersection can only lie in $S\tilde{\mathcal{V}}\cap S C(\rho ^{-1})_{K_{\infty }}$ . The variable $S$ generates a prime ideal in $\mathcal{O}_\pi [\![S,T]\!]$ . So, the $S$ -order is well defined. Let $F(T,S)$ be of minimal $S$ -order such that $F(T,S)u\in C(\rho ^{-1})_{K_{\infty }}$ , that is, there exists an element $c$ in $C(\rho ^{-1})_{K_{\infty }}$ such that $Sc=F(T,S)u$ . Note that $F(T,S)=SF'(T,S)$ for some $F'(S,T)$ . We obtain

\begin{align*} S(F'(T,S)u-c)=0. \end{align*}

As $E(\rho ^{-1})_{K_{\infty }}$ is torsion-free, this implies that $F'(T,S)u-c=0$ contradicting the minimality of the $S$ -order of $F(S,T)$ . Thus, $F(S,T)$ does not exist and $E(\rho ^{-1})_{K_{\infty }}\cap \tilde{\mathcal{V}}$ is trivial.

As an immediate consequence, we obtain the following result:

Corollary 6.5. The quotient

\begin{align*} U(\rho ^{-1})_{K_{\infty }}/(C(\rho )_{K_{\infty }}+\tilde{\mathcal{V}}) \end{align*}

is a torsion $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ -module.

Theorem 6.6. There is an equality of characteristic ideals

\begin{align*} \textrm{Char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(X(\rho ^{-1})_{K_{\infty }}/\Phi (\tilde{\mathcal{V}}))=\textrm{Char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(U(\rho ^{-1})_{K_{\infty }}/(\tilde{\mathcal{V}}+C(\rho ^{-1})_{K_{\infty }}). \end{align*}

Proof. Let $A_{\infty }$ be the projective limit of the $p$ -class groups of the intermediate fields of exponent $p^n$ of $\mathcal{K}/K(\mathfrak{f})$ . There is an exact sequence:

\begin{align*} 0\to E/C\to U/C\to X\to A_{\infty }\to 0. \end{align*}

Twisting by $\rho ^{-1}$ and using the fact that $\vert \Delta \vert$ is coprime to $p$ , we obtain the following exact sequence:

\begin{align*} 0&\to E(\rho ^{-1})_{K_{\infty }}/C(\rho ^{-1})_{K_{\infty }}\to U(\rho ^{-1})_{K_{\infty }}/C(\rho ^{-1})_{K_{\infty }} \\[5pt] &\to X(\rho ^{-1})_{K_{\infty }}\to A_{\infty }(\rho ^{-1})_{K_{\infty }}\to 0. \end{align*}

Using Lemma 6.4 this yields

(6.1) \begin{align} 0&\to E(\rho ^{-1})_{K_{\infty }}/C(\rho ^{-1})_{K_{\infty }}\to U(\rho ^{-1})_{K_{\infty }}/(C(\rho ^{-1})_{K_{\infty }}+\tilde{\mathcal{V}})\nonumber \\[5pt] &\to X(\rho ^{-1})_{K_{\infty }}/\Phi (\tilde{\mathcal{V}})\to A(\rho ^{-1})_{K_{\infty }}\to 0. \end{align}

By Corollary 6.5, all of these modules are in fact torsion. Using the fact that $\rho$ restricted to $\Delta$ is nontrivial, we can apply [11, Theorem 4.1] to see that $E(\rho ^{-1})_{K_{\infty }}/C(\rho ^{-1})_{K_{\infty }}$ and $A(\rho ^{-1})_{K_{\infty }}$ have the same characteristic ideal over the ring $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ . The claim now follows from (6.1).

We need the following sequence of lemmas from [13, Lemmas 6.4 and 6.5]. For an ideal $\mathfrak{A}$ in $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ , we write $\overline{\mathfrak{A}}$ for its image under the natural projection to $\Lambda \otimes{\mathcal{O}_\pi }$ .

Lemma 6.7. Suppose that $B$ is a finitely generated torsion $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ -module with no nonzero pseudo-null submodule. Let $\gamma$ be a topological generator for $\textrm{Gal}(K_{\infty }/K)$ . Then, $\overline{\textrm{char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(B)}\neq 0$ if and only if $B/(\gamma -1)B$ is a torsion $\Lambda \otimes \mathcal{O}_{\pi }$ -module. In this case,

\begin{align*} \textrm{Char}_{\Lambda \otimes \mathcal{O}_\pi }(B/(\gamma -1)B)=\overline{\textrm{Char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(B)}. \end{align*}

Lemma 6.8. Suppose that $B$ is a finitely generated $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ -module with no nonzero pseudo-null submodule. If $B'$ is a free $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ submodule of $B$ , then $B/B'$ has no nonzero pseudo-null $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ -submodule.

With these two lemmas, we can prove the following central theorem.

Theorem 6.9. There is an equality of characteristic ideals:

\begin{align*} \textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V}))=\textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(U(\rho ^{-1})_{K_c}/(\mathcal{V}+C(\rho ^{-1})_{K_c}). \end{align*}

Proof. Let $\tilde{\mathcal{V}}_{K_c}$ be the projection of $\tilde{\mathcal{V}}$ to the cyclotomic line. Recall that $Z$ was a prime element that is corpime to both sides of the equation in Theorem 6.9. Note that $\mathcal{V}/\tilde{\mathcal{V}}_{K_c}$ is annihilated by $Z^a$ for some $a$ . Therefore,

\begin{align*} (Z^e)\textrm{char}_{\Lambda \otimes{\mathcal{O}_\pi }}(U(\rho ^{-1})_{K_c}/(\mathcal{V}+C(\rho ^{-1})_{K_c})= \textrm{char}_{\Lambda \otimes{\mathcal{O}_\pi }}(U(\rho ^{-1})_{K_c}/(\tilde{\mathcal{V}}_{K_c}+C(\rho ^{-1})_{K_c}) \end{align*}

for some integer $e\le a$ . By construction $\tilde{\mathcal{V}}$ is free of rank $1$ over $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ . By Lemma 6.4, the quotient $\tilde{\mathcal{V}}+C(\rho ^{-1})_{K_{\infty }}$ is free of rank $2$ (for the freeness of $C(\rho ^{-1})_{K_{\infty }}$ see [13, Theorem 5.1] or [11, Theorem 7.7]). Hence, we can apply Lemma 6.8 to see that $U(\rho ^{-1})_{K_{{\infty }}}/(\tilde{\mathcal{V}}+C(\rho ^{-1})_{K_{\infty }})$ does not contain a nonzero pseudo-null submodule. By Lemma 6.7, we obtain

(6.2) \begin{align} &\textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(U(\rho ^{-1})_{K_c}/(\tilde{\mathcal{V}}_{K_c}+C(\rho ^{-1})_{K_c})\nonumber \\[5pt] &\quad =\overline{\textrm{Char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(U(\rho ^{-1})_{K_{\infty }}/(\tilde{\mathcal{V}}+C(\rho ^{-1})_{K_{\infty }}))}. \end{align}

Recall that the kernel of $\Phi$ is $E(\rho ^{-1})_{K_{\infty }}$ . By Lemma 6.4, the homomorphism $\Phi$ is injective on $\tilde{\mathcal{V}}$ and we obtain that $\Phi (\tilde{V})$ is free of rank one over $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ . Further, by [6, Theorem 2] $X(\rho ^{-1})_{K_{\infty }}$ has $\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]$ -rank one and does not contain a nonzero pseudo-null submodule. By Lemma 6.8, the quotient $X(\rho ^{-1})_{K_{\infty }}/\Phi (\tilde{\mathcal{V}})$ does not contain a nonzero pseudo-null submodule. Therefore, Lemma 6.7 implies

\begin{align*} \textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(X(\rho ^{-1})_{K_c}/\Phi (\tilde{\mathcal{V}}_{K_c}))=\overline{\textrm{Char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(X(\rho ^{-1})_{K_{\infty }}/\Phi (\tilde{\mathcal{V}}))}. \end{align*}

Using again that $\mathcal{V}/\tilde{\mathcal{V}}_{K_c}$ is annihilated by a power of $Z$ , we obtain

\begin{align*} (Z^g)\textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V}))= \overline{\textrm{Char}_{\mathcal{O}_\pi [\![\textrm{Gal}(K_{\infty }/K)]\!]}(X(\rho ^{-1})_{K_{\infty }}/\Phi (\tilde{\mathcal{V}}))} \end{align*}

for some integer $g$ . Combining the above identities of characteristic ideals with Theorem 6.6 gives

\begin{align*} (Z^g)\textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(X(\rho ^{-1})_{K_c}/\Phi (\mathcal{V}))=(Z^e)\textrm{Char}_{\Lambda \otimes{\mathcal{O}_\pi }}(U(\rho ^{-1})_{K_c}/(\mathcal{V}+C(\rho ^{-1})_{K_c}). \end{align*}

By the choice of $Z$ , we can deduce the desired equality.

7. The final argument

Combining Theorem 6.9 with Lemma 4.6, we are left to determine the characteristic ideal of $U(\rho ^{-1})/(\mathcal{V}+C(\rho ^{-1})_{K_c})$ as $\Lambda \otimes \mathcal{O}_\pi$ -module. We therefore obtain the following result.

Theorem 7.1. There is an equality of characteristic ideals

\begin{align*} \textrm{Char}_{\Lambda \otimes \mathcal{O}_\pi }(\textrm{Hom}_{\mathcal{O}}(\textrm{Sel}(K_c),K_{\pi }/\mathcal{O}_{\pi }))=(\mathcal{L}_{e_0}(z_{\textrm{kato}}(k-1))^{\Delta '})(\Lambda \otimes \mathcal{O}_{\pi })=L_p(f)^{\Delta '}. \end{align*}

Proof. We showed in Section 6:

\begin{align*} U(\rho ^{-1})_{K_{c}}/\mathcal{V}\cong \varprojlim _{{n\in \mathbb{N}}}H^1_{/f}(\mathbb{Q}_p(\zeta _{p^n}),T(k-1))^{\Delta '}\otimes \mathcal{O}_{\pi }. \end{align*}

By Lemma 5.14 and the properties of $z_{\textrm{kato}}$ (see the beginning of Section 6 including the proof of Lemma 6.3), the characteristic ideal of

\begin{align*} \textrm{Hom}_{\mathcal{O}}(\textrm{Sel}(K_c),K_{\pi }/\mathcal{O}_{\pi })\cong U(\rho ^{-1})/(\mathcal{V}+C(\rho ^{-1})_{K_c}) \end{align*}

is given by $\mathcal{L}(z_{\textrm{kato}})^{\Delta '}$ . By Lemma 5.18, this is precisely the $p$ -adic $L$ -function $L_p(f)^{\Delta '}$ .

Proof of Theorem 1.2. The theorem follows from taking invariants in Theorem 7.1.