Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T06:05:05.476Z Has data issue: false hasContentIssue false
  • English
  • Français

The kernel relation for a strict extension of certain regular semigroups

Published online by Cambridge University Press:  18 May 2009

Mario Petrich
Mario Petrich
Affiliation:
c/o J. E. Mills, Department of Mathematics, Seattle University, Seattle Washington 98122, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a regular semigroup and denote by 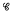(R) its congruence lattice. For 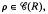, the kernel of pis the set ker 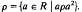. The relation K on 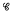(R) defined by λKp if ker λ = ker p is the kernel relation on 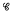(R). In general, K is a complete ∩-congruence but it is not a v-congruence. In view of the importance of the kernel-trace approach to the study of congruences on a regular semigroup (the trace of p is its restriction to idempotents of R), it is of considerable interest to determine necessary and sufficient conditions on R in order for K to be a congruence. This being in general a difficult task, one restricts attention to special classes of regular semigroups. For a background on this subject, consult [1].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 3 , September 1996 , pp. 347 - 357
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Pastijn, F. and Petrich, M., Congruences on regular semigroups, Trans. Amer. Math. Soc. 295 (1986), 607–633.CrossRefGoogle Scholar
2.Petrich, M., Congruences on extensions of semigroups, Duke Math. J. 34 (1967), 215–224.CrossRefGoogle Scholar
3.Petrich, M., The kernel relation for a retract extension of Brandt semigroups, Boll. Unione Mat. ltal. 5-B (1991), 1–19.Google Scholar
4.Petrich, M., The congruence lattice of an ideal extension of semigroups, Glasgow Math. J. 35 (1993), 39–50.CrossRefGoogle Scholar
5.Petrich, M., The kernel relation for certain regular semigroups, Boll. Unione Mat. ltal. 7-B (1993), 87–110.Google Scholar
6.Petrich, M., The congruence lattice of an extension of completely 0-simple semigroups, Acta Math. Hung. 64 (1994), 409–435.CrossRefGoogle Scholar