Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jameson, G. J. O.
2019.
Operator-valued Extensions of Matrix-norm Inequalities.
The American Mathematical Monthly,
Vol. 126,
Issue. 9,
p.
809.
Hovhannisyan, Karen V.
and
Imparato, Alberto
2024.
Energy conservation and fluctuation theorem are incompatible for quantum work.
Quantum,
Vol. 8,
Issue. ,
p.
1336.


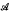 be either a
be either a 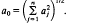 .
.