Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T01:20:55.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Lacunarity of Dedekind η-products

Published online by Cambridge University Press:  18 May 2009

Basil Gordon  and
Sinai Robins
Basil Gordon
Affiliation:
University of California, Los Angeles
Sinai Robins
Affiliation:
University of Northern Colorado, Greeley
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Dedekind η-function is defined by

where τ lies in the upper half plane ℋ = {tau;|Im(τ) > 0}, and x = e2πiτ. It is a modular form of weight ½ with a multiplier system. We define an η-product to be a function f (τ) of the form

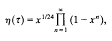
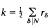where rδ ε ℤ. This is a modular form of weight with a multiplier system. The Fourier coefficients of η-products are related to many well-known number-theoretic functions, including partition functions and quadratic form representation numbers. They also arise from representations of the “monster” group [3] and the Mathieu group M24 [13]. The multiplicative structure of these Fourier coefficients has been extensively studied. Recent papers include [1], [4], [5] and [6]. Here we study the connections between the density of the non-zero Fourier coefficients of f(τ) and the representability of f(τ) as a linear combination of Hecke character forms (defined in Section 4 below). We first make the following definition.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 37 , Issue 1 , January 1995 , pp. 1 - 14
Copyright
Copyright © Glasgow Mathematical Journal Trust 1995

References

REFERENCES

1.Biagioli, A. J. F., η-products which are simultaneous eigenforms of Hecke operators, to appear.Google Scholar
2.Cohen, H. and Oesterlé, J., Dimension des espaces de formes modulaires, Springer Led Notes in Math. 627 (1976), 69–78.CrossRefGoogle Scholar
3.Conway, J. H. and Norton, S. P., Monstrous moonshine, Bull. London Math. Soc. 11 (1979), 308–339.CrossRefGoogle Scholar
4.Dummit, D., Kisilevsky, H. and McKay, J., Multiplicative products of η-functions, Contemporary Mathematics 45 (1985), 89–98.CrossRefGoogle Scholar
5.Gordon, B. and Hughes, K., Multiplicative properties of η-products II, to appear.Google Scholar
6.Gordon, B. and Sinor, D., Multiplicative properties of η-products, Springer Led. Notes in Math. 1395 (1988), 173–200.CrossRefGoogle Scholar
7.Hartshorne, R., Algebraic Geometry (Springer-Verlag, 1977).CrossRefGoogle Scholar
8.Kac, V. G., Infinite dimensional algebras, Dedekind's η-function, classical Mobius function and the Very Strange Formula, Advances in Mathematics 30 (1978), 85–136.CrossRefGoogle Scholar
9.Kac, V. G. and Peterson, D. H., Affine Lie algebras and Hecke modular forms, Bull. Amer. Math. Soc. (New Series) 3 (1980), 1057–1061.CrossRefGoogle Scholar
10.Koblitz, N., Introduction to Elliptic Curves and Modular Forms (Springer-Verlag, 1984).CrossRefGoogle Scholar
11.Landau, E., Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindestzahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate, Arch. Math. Phys. (3) 13 (1908), 30–312.Google Scholar
12.Ligozat, G., Courbes modulaires de genre 1, Bull. Soc. Math. France, Memoire 43 (1975), 1–80.Google Scholar
13.Mason, G., M24 and certain automorphic forms, Contemporary Mathematics 45 (1985), 223–244.CrossRefGoogle Scholar
14.Ribet, K., Galois representations attached to eigenforms of Nebentypus, Springer Led. Notes in Math. 601 (1977), 17–52.Google Scholar
15.Serre, J.-P., Divisibilité de certaines fonctions arithmétiques, Enseignement Math. (2) 22 (1976), 227–260.Google Scholar
16.Serre, J.-P., Quelques applications du théorème de densité de Chebotarev, Publ. Math. I.E.H.S. 54 (1981), 123–201.CrossRefGoogle Scholar
17.Serre, J.-P., Sur la lacunarité des puissances de η, Glasgow Math. J. 27 (1985), 203–221.CrossRefGoogle Scholar
18.Tunnel, J., A Classical diophantine problem and modular forms of wt. 3/2, Inventiones Math. 72 (1983), 323–334.CrossRefGoogle Scholar