Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McAlister, D.B.
1980.
Semigroups.
p.
1.
Jones, Peter R.
1990.
Lattices, Semigroups, and Universal Algebra.
p.
115.
Horadam, K. J.
and
Farr, G. E.
1994.
The conjugacy problem for HNN extensions with infinite cyclic associated groups.
Proceedings of the American Mathematical Society,
Vol. 120,
Issue. 4,
p.
1009.

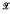 ,
, 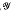 ), for some semilattice
), for some semilattice 