Hostname: page-component-7f64f4797f-d7bbv Total loading time: 0 Render date: 2025-11-04T08:22:09.576Z Has data issue: false hasContentIssue false
  • English
  • Français

LEFT ℓ1-FACTORABLE POLYNOMIALS

Published online by Cambridge University Press:  01 September 2009

RAFFAELLA CILIA  and
JOAQUÍN M. GUTIÉRREZ
RAFFAELLA CILIA
Affiliation:
Dipartimento di Matematica, Facoltà di Scienze, Università di Catania, Viale Andrea Doria 6, 95125 Catania, Italy e-mail: cilia@dmi.unict.it
JOAQUÍN M. GUTIÉRREZ
Affiliation:
Departamento de Matemática Aplicada, ETS de Ingenieros Industriales, Universidad Politécnica de Madrid, C. José Gutiérrez Abascal 2, 28006 Madrid, Spain e-mail: jgutierrez@etsii.upm.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A polynomial P ∈ (kE, F) is left ℓ1-factorable if there are a polynomial Q ∈ (kE, ℓ1) and an operator L ∈ 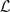(ℓ1, F) such that P = L ○ Q. We characterise the Radon–Nikodým property by the left ℓ1-factorisation of polynomials on L1(μ). We study the left ℓ1-factorisation of nuclear, compact and Pietsch integral polynomials. For Pietsch integral polynomials, we introduce the left integral ℓ1-factorisation property, obtaining a second polynomial characterisation of the Radon–Nikodým property and showing that it plays a role somehow comparable, in this setting, to nuclearity of operators. A characterisation of 1-spaces is also given in terms of the left compact ℓ1-factorisation of polynomials.

Keywords

Primary 46G25secondary 47H6046B2046B22

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 3 , September 2009 , pp. 631 - 649
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Albiac, F. and Kalton, N. J., Topics in Banach space theory, Graduate Texts in Mathematics, vol. 233 (Springer, New York, 2006).Google Scholar
2.Alencar, R., Multilinear mappings of nuclear and integral type, Proc. Am. Math. Soc. 94 (1985), 33–38.CrossRefGoogle Scholar
3.Alencar, R., On reflexivity and basis for (mE), Math. Proc. R. Ir. Acad. 85A (1985), 131–138.Google Scholar
4.Ansemil, J. M. and Floret, K., The symmetric tensor product of a direct sum of locally convex spaces, Studia Math. 129 (1998), 285–295.Google Scholar
5.Aron, R. M., Hervés, C. and Valdivia, M., Weakly continuous mappings on Banach spaces, J. Funct. Anal. 52 (1983), 189–204.CrossRefGoogle Scholar
6.Aron, R. M. and Prolla, J. B., Polynomial approximation of differentiable functions on Banach spaces, J. Reine Angew. Math. 313 (1980), 195–216.Google Scholar
7.Blasco, F., Complementation in spaces of symmetric tensor products and polynomials, Studia Math. 123 (1997), 165–173.CrossRefGoogle Scholar
8.Botelho, G. and Pellegrino, D. M., Two new properties of ideals of polynomials and applications, Indag. Math. (N.S.) 16 (2005), 157–169.CrossRefGoogle Scholar
9.Carando, D., Extendible polynomials on Banach spaces, J. Math. Anal. Appl. 233 (1999), 359–372.CrossRefGoogle Scholar
10.Carando, D., Dimant, V. and Muro, S., Coherent sequences of Banach ideals of polynomials, to appear in Math. Nachr.Google Scholar
11.Carando, D. and Lassalle, S., E′ and its relation with vector-valued functions on E, Ark. Math. 42 (2004), 283–300.CrossRefGoogle Scholar
12.Cilia, R., D'Anna, M. and Gutiérrez, J. M., Polynomial characterization of ∞-spaces, J. Math. Anal. Appl. 275 (2002), 900–912.CrossRefGoogle Scholar
13.Cilia, R. and Gutiérrez, J. M., Nuclear and integral polynomials, J. Austral. Math. Soc. 76 (2004), 269–280.CrossRefGoogle Scholar
14.Cilia, R. and Gutiérrez, J. M., Extension and lifting of weakly continuous polynomials, Studia Math. 169 (2005), 229–241.CrossRefGoogle Scholar
15.Cilia, R. and Gutiérrez, J. M., Integral and S-factorizable multilinear mappings, Proc. R. Soc. Edinb. 136A (2006), 115–137.CrossRefGoogle Scholar
16.Cilia, R. and Gutiérrez, J. M., Ideals of integral and r-factorable polynomials, to appear in Bol. Soc. Mat. Mexicana.Google Scholar
17.Defant, A. and Floret, K., Tensor norms and operator ideals, Mathematics Studies, vol. 176 (North-Holland, Amsterdam, 1993).Google Scholar
18.Diestel, J. and Uhl, J. J. Jr., Vector measures, Mathematical Surveys and Monographs, vol. 15 (American Mathematical Society, Providence RI, 1977).CrossRefGoogle Scholar
19.Dineen, S., Complex analysis on infinite dimensional spaces, Springer Monographs in Mathematics (Springer, Berlin, 1999).CrossRefGoogle Scholar
20.Figiel, T., Factorization of compact operators and applications to the approximation problem, Studia Math. 45 (1973), 191–210.CrossRefGoogle Scholar
21.Floret, K., Natural norms on symmetric tensor products of normed spaces, Note Mat. 17 (1997), 153–188.Google Scholar
22.Floret, K., Minimal ideals of n-homogeneous polynomials on Banach spaces, Results Math. 39 (2001), 201–217.CrossRefGoogle Scholar
23.Floret, K., On ideals of n-homogeneous polynomials on Banach spaces, in Topological algebras with applications to differential geometry and mathematical physics (Athens, 1999) (Strantzalos, P. and Fragoulopoulou, M., Editors) (University of Athens, Athens, 2002), 19–38.Google Scholar
24.Floret, K. and Hunfeld, S., Ultrastability of ideals of homogeneous polynomials and multilinear mappings on Banach spaces, Proc. Am. Math. Soc. 130 (2002), 1425–1435.CrossRefGoogle Scholar
25.González, M. and Gutiérrez, J. M., Factorization of weakly continuous holomorphic mappings, Studia Math. 118 (1996), 117–133.Google Scholar
26.Johnson, W. B., Factoring compact operators, Isr. J. Math. 9 (1971), 337–345.CrossRefGoogle Scholar
27.Lindenstrauss, J. and Pełzyński, A., Absolutely summing operators in p-spaces and their applications, Studia Math. 29 (1968), 275–326.CrossRefGoogle Scholar
28.Lindenstrauss, J. and Rosenthal, H. P., The p-spaces, Isr. J. Math. 7 (1969), 325–349.CrossRefGoogle Scholar
29.Mujica, J., Complex analysis in Banach spaces, Mathematics Studies, vol. 120 (North-Holland, Amsterdam, 1986).Google Scholar
30.Rudin, W., Principles of mathematical analysis (McGraw-Hill, New York, 1976).Google Scholar
31.Ryan, R. A., Applications of topological tensor products to infinite dimensional holomorphy, PhD Thesis (Trinity College, Dublin, 1980).Google Scholar
32.Ryan, R. A., Weakly compact holomorphic mappings on Banach spaces, Pac. J. Math. 131 (1988), 179–190.CrossRefGoogle Scholar
33.Ryan, R. A., Introduction to tensor products of Banach spaces, Springer Monographs in Mathematics (Springer, London, 2002).CrossRefGoogle Scholar
34.Villanueva, I., Integral mappings between Banach spaces, J. Math. Anal. Appl. 279 (2003), 56–70.CrossRefGoogle Scholar
35.Wojtaszczyk, P., Banach spaces for analysts, Cambridge Studies in Advanced Mathematics, vol. 25 (Cambridge University Press, Cambridge, UK 1991).CrossRefGoogle Scholar