No CrossRef data available.
Published online by Cambridge University Press: 09 August 2007
In this paper we study linear fractional relations defined in the following way. Let 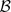 i,
i, 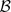 'i, i = 1,2, be Banach spaces. We denote the space of bounded linear operators by
'i, i = 1,2, be Banach spaces. We denote the space of bounded linear operators by 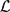 . Let T ε
. Let T ε 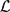 (
(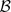 1 ⊕
1 ⊕ 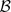 2,
2, 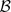 '1 ⊕
'1 ⊕ 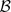 '2). To each such operator there corresponds a 2 × 2 operator matrix of the form(*)
'2). To each such operator there corresponds a 2 × 2 operator matrix of the form(*)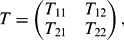 where T ij ε
where T ij ε 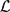 (
(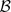 j ,
j , 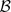 'i . For each such T we define a set-valued map G T from
'i . For each such T we define a set-valued map G T from 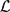 (
(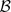 1,
1, 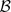 2) into the set of closed affine subspaces of
2) into the set of closed affine subspaces of 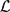 (
(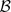 '1,
'1, 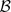 '2) by
'2) by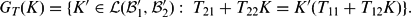
The map G T is called a linear fractional relation.
The paper is devoted to the following two problems.
• Characterization of operator matrices of the form (*) for which the set G T(K) is non-empty for each K in some open ball of the space 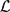 (
(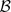 1,
1,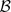 2).
2).
• Characterizations of quadruples (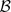 1,
1, 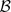 2,
2,  '1,
'1,  '2) of Banach spaces such that linear fractional relations defined for such spaces satisfy the natural analogue of the Liouville theorem “a bounded entire function is constant”.
'2) of Banach spaces such that linear fractional relations defined for such spaces satisfy the natural analogue of the Liouville theorem “a bounded entire function is constant”.