Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Garcı́a, Domingo
and
Mujica, Jorge
1997.
Quasi-Normable Preduals of Spaces of Holomorphic Functions.
Journal of Mathematical Analysis and Applications,
Vol. 208,
Issue. 1,
p.
171.
Boyd, Christopher
and
Dineen, SeÁN
1998.
Compact Sets of Holomorphic Mappings.
Mathematische Nachrichten,
Vol. 193,
Issue. 1,
p.
27.
Boyd, Christopher
2004.
HOLOMORPHIC FUNCTIONS AND THE BB-PROPERTY ON PRODUCT SPACES.
Journal of the Korean Mathematical Society,
Vol. 41,
Issue. 1,
p.
39.

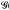 (
(