Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Golan, Jonathan S.
and
Miller, Robert W.
1978.
Cotorsionfree modules and colocalizations.
Communications in Algebra,
Vol. 6,
Issue. 12,
p.
1217.
Markov, V. T.
Mikhalev, A. V.
Skornyakov, L. A.
and
Tuganbaev, A. A.
1983.
Modules.
Journal of Soviet Mathematics,
Vol. 23,
Issue. 6,
p.
2642.


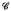 is a category, we shall abuse notation and write “
is a category, we shall abuse notation and write “