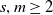1. Introduction
Groups acting on rooted trees have drawn a great deal of attention over the last couple of decades because they exhibit prominent features and solve several long-standing problems in group theory. The initial examples studied were Grigorchuk’s groups of intermediate word growth ([Reference Grigorchuk13]; answering Milnor’s question) and Gupta and Sidki’s examples of finitely generated infinite
![]() $p$
-groups ([Reference Gupta and Sidki17]; providing an explicit family of
$p$
-groups ([Reference Gupta and Sidki17]; providing an explicit family of
![]() $2$
-generated counterexamples to the general Burnside problem). Ever since, attempts have been made to characterise and generalise the groups of automorphisms of rooted trees. Today, the Grigorchuk groups and the Gupta–Sidki groups are known as the first examples of groups in the family of branch groups. Branch groups are groups acting level-transitively on a spherically homogeneous rooted tree
$2$
-generated counterexamples to the general Burnside problem). Ever since, attempts have been made to characterise and generalise the groups of automorphisms of rooted trees. Today, the Grigorchuk groups and the Gupta–Sidki groups are known as the first examples of groups in the family of branch groups. Branch groups are groups acting level-transitively on a spherically homogeneous rooted tree
![]() $T$
and having subnormal subgroups similar to that of the full automorphism group
$T$
and having subnormal subgroups similar to that of the full automorphism group
![]() $\textrm{Aut}\, T$
of the tree
$\textrm{Aut}\, T$
of the tree
![]() $T$
; see Section 2 for definitions. The groups studied in this paper belong to a more general class of groups, the weakly branch groups, obtained by weakening some of the algebraic properties of branch groups; cf. [Reference Bartholdi, Grigorchuk and Sunić2].
$T$
; see Section 2 for definitions. The groups studied in this paper belong to a more general class of groups, the weakly branch groups, obtained by weakening some of the algebraic properties of branch groups; cf. [Reference Bartholdi, Grigorchuk and Sunić2].
The Basilica group is a
![]() $2$
-generated weakly branch, but not branch, group acting on the binary rooted tree, which was introduced by Grigorchuk and Żuk in refs. [Reference Grigorchuk and Żuk14] and [Reference Grigorchuk and Żuk15]. It is the first known example of an amenable [Reference Bartholdi and Virág4] but not sub-exponentially amenable group [Reference Grigorchuk and Żuk15]. In contrast to the Grigorchuk and the Gupta–Sidki groups, the Basilica group is torsion-free and has exponential word growth [Reference Grigorchuk and Żuk15]. Moreover, it is the iterated monodromy group of the complex polynomial
$2$
-generated weakly branch, but not branch, group acting on the binary rooted tree, which was introduced by Grigorchuk and Żuk in refs. [Reference Grigorchuk and Żuk14] and [Reference Grigorchuk and Żuk15]. It is the first known example of an amenable [Reference Bartholdi and Virág4] but not sub-exponentially amenable group [Reference Grigorchuk and Żuk15]. In contrast to the Grigorchuk and the Gupta–Sidki groups, the Basilica group is torsion-free and has exponential word growth [Reference Grigorchuk and Żuk15]. Moreover, it is the iterated monodromy group of the complex polynomial
![]() $z^2-1$
; see [Reference Nekrashevych21, Section 6.12.1]. The generators of the Basilica group are recursively defined as follows:
$z^2-1$
; see [Reference Nekrashevych21, Section 6.12.1]. The generators of the Basilica group are recursively defined as follows:
where
![]() $\sigma$
is the cyclic permutation which swaps the subtrees rooted at the first level of the binary rooted tree, and
$\sigma$
is the cyclic permutation which swaps the subtrees rooted at the first level of the binary rooted tree, and
![]() $(x,y)$
represents the independent action on the two maximal subtrees, where
$(x,y)$
represents the independent action on the two maximal subtrees, where
![]() $x,y\in \textrm{Aut}\, T$
. Recently, Petschick and Rajeev [Reference Petschick and Rajeev23] introduced a construction which relates the Basilica group and the one-generated dyadic odometer
$x,y\in \textrm{Aut}\, T$
. Recently, Petschick and Rajeev [Reference Petschick and Rajeev23] introduced a construction which relates the Basilica group and the one-generated dyadic odometer
![]() $\mathcal{O}_2$
(also known as the adding machine). Let
$\mathcal{O}_2$
(also known as the adding machine). Let
![]() $m, \,s \geq 2$
be integers and let
$m, \,s \geq 2$
be integers and let
![]() $G$
be a subgroup of the automorphism group
$G$
be a subgroup of the automorphism group
![]() $\textrm{Aut}\, T$
of the
$\textrm{Aut}\, T$
of the
![]() $m$
-adic tree
$m$
-adic tree
![]() $T$
. The
$T$
. The
![]() $s$
th Basilica group of
$s$
th Basilica group of
![]() $G$
is given by
$G$
is given by
![]() $\textrm{Bas}_s(G) = \langle \beta ^s_i(g)\mid g \in G, \, i \in \{0,1,\dots, s-1\}\,\rangle$
, where
$\textrm{Bas}_s(G) = \langle \beta ^s_i(g)\mid g \in G, \, i \in \{0,1,\dots, s-1\}\,\rangle$
, where
![]() $\beta _i^s\,{:}\, \textrm{Aut}\, T \rightarrow \textrm{Aut}\, T$
are monomorphisms given by
$\beta _i^s\,{:}\, \textrm{Aut}\, T \rightarrow \textrm{Aut}\, T$
are monomorphisms given by
where
![]() $g_x$
is the restriction of
$g_x$
is the restriction of
![]() $g$
to the subtree rooted at a first-level vertex
$g$
to the subtree rooted at a first-level vertex
![]() $x\in \{0,\ldots,m-1\}$
, and
$x\in \{0,\ldots,m-1\}$
, and
![]() $g^\epsilon$
is the local action of the element
$g^\epsilon$
is the local action of the element
![]() $g$
at the root of
$g$
at the root of
![]() $T$
. (In ref. [Reference Petschick and Rajeev23], the generators
$T$
. (In ref. [Reference Petschick and Rajeev23], the generators
![]() $\beta _i^s(g)$
, for
$\beta _i^s(g)$
, for
![]() $i \in \{1,\dots,s-1\}$
, are defined along the leftmost spine and the element
$i \in \{1,\dots,s-1\}$
, are defined along the leftmost spine and the element
![]() $g^\epsilon$
is acting from the left; however, the corresponding
$g^\epsilon$
is acting from the left; however, the corresponding
![]() $s$
th Basilica group is isomorphic to the one defined here). We obtain the classical Basilica group by applying the operator
$s$
th Basilica group is isomorphic to the one defined here). We obtain the classical Basilica group by applying the operator
![]() $\textrm{Bas}_2$
to the dyadic odometer as follows: let
$\textrm{Bas}_2$
to the dyadic odometer as follows: let
![]() $c = (1,c) \sigma$
be the automorphism of the binary rooted tree generating the dyadic odometer. Then, the generators of the Basilica group are given by
$c = (1,c) \sigma$
be the automorphism of the binary rooted tree generating the dyadic odometer. Then, the generators of the Basilica group are given by
This gives a natural generalisation of the Basilica group given by
![]() $\textrm{Bas}_s(\mathcal{O}_m)$
for every pair of integers
$\textrm{Bas}_s(\mathcal{O}_m)$
for every pair of integers
![]() $m\,, s \geq 2$
. Here,
$m\,, s \geq 2$
. Here,
![]() $\mathcal{O}_m$
is the
$\mathcal{O}_m$
is the
![]() $m$
-adic odometer, which is an embedding of the infinite cyclic group into the automorphism group of the
$m$
-adic odometer, which is an embedding of the infinite cyclic group into the automorphism group of the
![]() $m$
-adic tree
$m$
-adic tree
![]() $T$
, and is generated by
$T$
, and is generated by
where
![]() $\sigma = (0 \; 1 \; \cdots \; m-1)$
is the
$\sigma = (0 \; 1 \; \cdots \; m-1)$
is the
![]() $m$
-cycle that cyclically permutes the
$m$
-cycle that cyclically permutes the
![]() $m$
subtrees rooted at the first level of
$m$
subtrees rooted at the first level of
![]() $T$
. The generalised Basilica groups
$T$
. The generalised Basilica groups
![]() $\textrm{Bas}_s(\mathcal{O}_m)$
resemble the classical Basilica group, as they are weakly branch, but not branch, torsion-free groups of exponential word growth [Reference Petschick and Rajeev23, Theorem 1.6]. They are also weakly regular branch over their derived subgroup.
$\textrm{Bas}_s(\mathcal{O}_m)$
resemble the classical Basilica group, as they are weakly branch, but not branch, torsion-free groups of exponential word growth [Reference Petschick and Rajeev23, Theorem 1.6]. They are also weakly regular branch over their derived subgroup.
Now, as we will see below, the generalised Basilica groups lie in the set of iterated monodromy groups of post-critically finite complex polynomials, where a polynomial
![]() $f$
is post-critically finite if the orbit of the critical point 0 under iterations of
$f$
is post-critically finite if the orbit of the critical point 0 under iterations of
![]() $f$
is finite. Iterated monodromy groups are more naturally defined in terms of self-coverings of topological spaces, as done in ref. [Reference Nekrashevych21, Chapter 5], and these groups are of interest since they encode information about the dynamics of such self-coverings. However, below we will only abstractly define a subfamily of iterated monodromy groups that are of interest to us, and we only study their algebraic properties. Therefore, we refer the reader to [Reference Nekrashevych21] for more information about iterated monodromy groups in general.
$f$
is finite. Iterated monodromy groups are more naturally defined in terms of self-coverings of topological spaces, as done in ref. [Reference Nekrashevych21, Chapter 5], and these groups are of interest since they encode information about the dynamics of such self-coverings. However, below we will only abstractly define a subfamily of iterated monodromy groups that are of interest to us, and we only study their algebraic properties. Therefore, we refer the reader to [Reference Nekrashevych21] for more information about iterated monodromy groups in general.
We note that the iterated monodromy groups of the quadratic polynomials
![]() $f(z) = z^2+c$
have been studied in more depth. In ref. [Reference Bartholdi and Nekrashevych3], Bartholdi and Nekrashevych identified the iterated monodromy groups of post-critically finite quadratic polynomials
$f(z) = z^2+c$
have been studied in more depth. In ref. [Reference Bartholdi and Nekrashevych3], Bartholdi and Nekrashevych identified the iterated monodromy groups of post-critically finite quadratic polynomials
![]() $f(z) = z^2+c$
. Among those groups, we are interested in the groups
$f(z) = z^2+c$
. Among those groups, we are interested in the groups
![]() $\mathfrak{K(v)}$
, which are defined as below.
$\mathfrak{K(v)}$
, which are defined as below.
Let
![]() $s \geq 2$
and
$s \geq 2$
and
![]() ${\mathfrak{v}} = x_0\cdots x_{s-2}$
be a word over the alphabet
${\mathfrak{v}} = x_0\cdots x_{s-2}$
be a word over the alphabet
![]() $X = \{0,1\}.$
The group
$X = \{0,1\}.$
The group
![]() $\mathfrak{K(v)}$
is a subgroup of automorphisms of the binary rooted tree generated by the elements
$\mathfrak{K(v)}$
is a subgroup of automorphisms of the binary rooted tree generated by the elements
![]() $a_0,\dots,a_{s-1}$
, which are defined as
$a_0,\dots,a_{s-1}$
, which are defined as
 \begin{align*} a_0 = (1,a_{s-1}) \sigma, && a_{i+1} = \begin{cases} (a_{i},1) &\text{if } x_i = 0, \\ (1, a_{i}) &\text{if } x_i =1, \end{cases} \end{align*}
\begin{align*} a_0 = (1,a_{s-1}) \sigma, && a_{i+1} = \begin{cases} (a_{i},1) &\text{if } x_i = 0, \\ (1, a_{i}) &\text{if } x_i =1, \end{cases} \end{align*}
for
![]() $i \in{\{0,1,\ldots, s-2\}}$
. The quadratic polynomial associated with
$i \in{\{0,1,\ldots, s-2\}}$
. The quadratic polynomial associated with
![]() $\mathfrak{K(v)}$
can be precisely defined in terms of
$\mathfrak{K(v)}$
can be precisely defined in terms of
![]() $\mathfrak{v}$
; see [Reference Bartholdi and Nekrashevych3, Section 5]. Note that if
$\mathfrak{v}$
; see [Reference Bartholdi and Nekrashevych3, Section 5]. Note that if
![]() $s=1$
, then
$s=1$
, then
![]() $\mathfrak{v}$
is the empty word, then
$\mathfrak{v}$
is the empty word, then
![]() $\mathfrak{K}(\varnothing )$
is just the cyclic group
$\mathfrak{K}(\varnothing )$
is just the cyclic group
![]() $\mathbb{Z}$
. Notice that
$\mathbb{Z}$
. Notice that
![]() $\mathfrak{K}(1)$
is the classical Basilica group. Furthermore, by setting
$\mathfrak{K}(1)$
is the classical Basilica group. Furthermore, by setting
![]() ${\mathfrak{v}} = 1 \overset{s^{\prime}}\dots 1$
, we get that
${\mathfrak{v}} = 1 \overset{s^{\prime}}\dots 1$
, we get that
![]() $\mathfrak{K(v)} = \textrm{Bas}_{s^{\prime}+1}(\mathcal{O}_2)$
, for
$\mathfrak{K(v)} = \textrm{Bas}_{s^{\prime}+1}(\mathcal{O}_2)$
, for
![]() ${s^{\prime}}\in \mathbb{N}$
. The group
${s^{\prime}}\in \mathbb{N}$
. The group
![]() $\mathfrak{K(v)}$
has a corresponding so-called kneading sequence, by which the symbolic dynamics of quadratic complex polynomials are usually studied; see [Reference Bartholdi and Nekrashevych3] for more information.
$\mathfrak{K(v)}$
has a corresponding so-called kneading sequence, by which the symbolic dynamics of quadratic complex polynomials are usually studied; see [Reference Bartholdi and Nekrashevych3] for more information.
The recurrence relations in the definition of
![]() $\mathfrak{K(v)}$
above suggests that one can generalise this notion to groups acting on the
$\mathfrak{K(v)}$
above suggests that one can generalise this notion to groups acting on the
![]() $m$
-adic tree, for any
$m$
-adic tree, for any
![]() $m\ge 2$
. Let
$m\ge 2$
. Let
![]() ${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
![]() $X = \{0,1,\dots,m-1\}$
. Define
$X = \{0,1,\dots,m-1\}$
. Define
for
![]() $i \in{\{0,1,\ldots, s-2\}}$
, and
$i \in{\{0,1,\ldots, s-2\}}$
, and
![]() $\mathfrak{K(v)}$
as the group defined by the elements
$\mathfrak{K(v)}$
as the group defined by the elements
![]() $a_0,\dots,a_{s-1}$
. Then, for
$a_0,\dots,a_{s-1}$
. Then, for
![]() ${\mathfrak{v}} = 1 \overset{s^{\prime}}\dots 1$
, we have
${\mathfrak{v}} = 1 \overset{s^{\prime}}\dots 1$
, we have
![]() $\mathfrak{K(v)} = \textrm{Bas}_{s^{\prime}+1}(\mathcal{O}_m)$
.
$\mathfrak{K(v)} = \textrm{Bas}_{s^{\prime}+1}(\mathcal{O}_m)$
.
We establish the following basic properties of the groups
![]() $\mathfrak{K(v)}$
.
$\mathfrak{K(v)}$
.
Theorem 1.1.
Let
![]() $m,s\ge 2$
be positive integers, and let
$m,s\ge 2$
be positive integers, and let
![]() ${\mathfrak{v}} = x_0\cdots x_{s-2}$
be a word in the alphabet
${\mathfrak{v}} = x_0\cdots x_{s-2}$
be a word in the alphabet
![]() $X=\{0,1,\ldots, m-1\}$
. Then for the group
$X=\{0,1,\ldots, m-1\}$
. Then for the group
![]() $\mathfrak{K(v)}$
defined by
$\mathfrak{K(v)}$
defined by
![]() $\mathfrak{v}$
, the following assertions hold:
$\mathfrak{v}$
, the following assertions hold:
-
(i)
 $\mathfrak{K(v)}$
is an iterated monodromy group of a post-critically finite polynomial;
$\mathfrak{K(v)}$
is an iterated monodromy group of a post-critically finite polynomial;
-
(ii)
 $\mathfrak{K(v)}$
is super strongly fractal and level-transitive;
$\mathfrak{K(v)}$
is super strongly fractal and level-transitive;
-
(iii)
 $\mathfrak{K(v)}$
is not branch, but is weakly regular branch over its commutator subgroup
$\mathfrak{K(v)}$
is not branch, but is weakly regular branch over its commutator subgroup
 $\mathfrak{K(v)}^{\prime}$
;
$\mathfrak{K(v)}^{\prime}$
; -
(iv)
 $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime} \cong \mathbb{Z}^s$
;
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime} \cong \mathbb{Z}^s$
; -
(v)
 $\mathfrak{K(v)}$
is torsion-free;
$\mathfrak{K(v)}$
is torsion-free;
-
(vi)
 $\mathfrak{K(v)}$
is contracting;
$\mathfrak{K(v)}$
is contracting;
-
(vii)
 $\mathfrak{K(v)}$
has exponential word growth.
$\mathfrak{K(v)}$
has exponential word growth.
The above results, apart from part (ii), were known for the case
![]() $m=2$
; see [Reference Bartholdi and Nekrashevych3, Section 3]. We note that the fact that the groups
$m=2$
; see [Reference Bartholdi and Nekrashevych3, Section 3]. We note that the fact that the groups
![]() $\mathfrak{K(v)}$
are contracting already follows from [Reference Bondarenko and Nekrashevych7], but we give a self-contained proof which yields more information about the contracting property of the groups. The property of exponential word growth will not be utilised in this paper, so we instead refer the reader to [Reference Bartholdi, Grigorchuk and Sunić2, Chapter 10] for the definition.
$\mathfrak{K(v)}$
are contracting already follows from [Reference Bondarenko and Nekrashevych7], but we give a self-contained proof which yields more information about the contracting property of the groups. The property of exponential word growth will not be utilised in this paper, so we instead refer the reader to [Reference Bartholdi, Grigorchuk and Sunić2, Chapter 10] for the definition.
In this paper, we study the maximal subgroups of
![]() $\mathfrak{K(v)}$
for constant words
$\mathfrak{K(v)}$
for constant words
![]() $\mathfrak{v}$
; the case of non-constant words prove to be much more difficult and would require a different approach. The study of maximal subgroups of branch groups was initiated by Pervova [Reference Pervova22], where she proved that the torsion Grigorchuk groups do not contain maximal subgroups of infinite index. Thenceforth, attempts have been made to generalise the results and techniques from [Reference Pervova22], for instance see [Reference Alexoudas, Klopsch and Thillaisundaram1], [Reference Klopsch and Thillaisundaram20], and [Reference Francoeur10]. Among which our interest lies in the work of Francoeur [Reference Francoeur10] (or see [Reference Francoeur9, Section 8.4]), who provided a strategy to study the maximal subgroups of weakly branch groups. In particular, he proved that the classical Basilica group does not contain maximal subgroups of infinite index. Following this technique, we prove that
$\mathfrak{v}$
; the case of non-constant words prove to be much more difficult and would require a different approach. The study of maximal subgroups of branch groups was initiated by Pervova [Reference Pervova22], where she proved that the torsion Grigorchuk groups do not contain maximal subgroups of infinite index. Thenceforth, attempts have been made to generalise the results and techniques from [Reference Pervova22], for instance see [Reference Alexoudas, Klopsch and Thillaisundaram1], [Reference Klopsch and Thillaisundaram20], and [Reference Francoeur10]. Among which our interest lies in the work of Francoeur [Reference Francoeur10] (or see [Reference Francoeur9, Section 8.4]), who provided a strategy to study the maximal subgroups of weakly branch groups. In particular, he proved that the classical Basilica group does not contain maximal subgroups of infinite index. Following this technique, we prove that
![]() $\mathfrak{K(v)}$
, for constant words
$\mathfrak{K(v)}$
, for constant words
![]() $\mathfrak{v}$
, do not admit maximal subgroups of infinite index.
$\mathfrak{v}$
, do not admit maximal subgroups of infinite index.
Theorem 1.2.
Let
![]() $m,s\ge 2$
be positive integers, and let
$m,s\ge 2$
be positive integers, and let
![]() ${\mathfrak{v}}=t\,\overset{s-1}{\dots }\,t$
be the constant word for some
${\mathfrak{v}}=t\,\overset{s-1}{\dots }\,t$
be the constant word for some
![]() $t\in{\{0,1,\ldots,m-1\}}$
. Then, the group
$t\in{\{0,1,\ldots,m-1\}}$
. Then, the group
![]() $\mathfrak{K(v)}$
does not admit a maximal subgroup of infinite index.
$\mathfrak{K(v)}$
does not admit a maximal subgroup of infinite index.
Due to the different properties of the family
![]() $\mathfrak{K(v)}$
, the final stages of our proof differ from previously seen results; compare Theorem 5.6. This is also the first time that maximal subgroups of a weakly branch, but not branch, group
$\mathfrak{K(v)}$
, the final stages of our proof differ from previously seen results; compare Theorem 5.6. This is also the first time that maximal subgroups of a weakly branch, but not branch, group
![]() $G$
have been considered for a group
$G$
have been considered for a group
![]() $G$
with more than
$G$
with more than
![]() $2$
generators.
$2$
generators.
It is interesting to note that there are currently no examples of finitely generated weakly branch, but not branch, groups with maximal subgroups of infinite index. There are only examples of finitely generated branch groups with maximal subgroups of infinite index; see [Reference Bondarenko6, Reference Francoeur and Garrido11, Reference Kionke and Schesler19]. It remains to be seen whether being a finitely generated weakly branch group with maximal subgroups of infinite index implies the group is branch.
Furthermore, in all known examples of finitely generated weakly branch, but not branch, groups with maximal subgroups only of finite index, these groups have maximal subgroups that are not normal; compare Remark 5.8 and [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Reference Francoeur and Thillaisundaram12]. Therefore, it is also natural to ask if there exists a finitely generated weakly branch, but not branch, group with all maximal subgroups of finite index and normal.
Organisation. Section 2 contains preliminary material on groups acting on the
![]() $m$
-adic tree, and Section 3 establishes basic properties of the groups
$m$
-adic tree, and Section 3 establishes basic properties of the groups
![]() $\mathfrak{K(v)}$
, that is, we prove Theorem 1.1. In Section 4, we record some length-reducing properties of a large subfamily of the groups
$\mathfrak{K(v)}$
, that is, we prove Theorem 1.1. In Section 4, we record some length-reducing properties of a large subfamily of the groups
![]() $\mathfrak{K(v)}$
, and in Section 5, we prove Theorem 1.2.
$\mathfrak{K(v)}$
, and in Section 5, we prove Theorem 1.2.
2. Preliminaries
By
![]() $\mathbb{N}$
we denote the set of positive integers, and by
$\mathbb{N}$
we denote the set of positive integers, and by
![]() $\mathbb{N}_0$
the set of non-negative integers.
$\mathbb{N}_0$
the set of non-negative integers.
Let
![]() $m\in \mathbb{N}_{\ge 2}$
and let
$m\in \mathbb{N}_{\ge 2}$
and let
![]() $T = T_m$
be the
$T = T_m$
be the
![]() $m$
-adic tree, that is, a rooted tree where all vertices have
$m$
-adic tree, that is, a rooted tree where all vertices have
![]() $m$
children. Using the alphabet
$m$
children. Using the alphabet
![]() $X = \{0,1,\ldots,m-1\}$
, the vertices
$X = \{0,1,\ldots,m-1\}$
, the vertices
![]() $u_\omega$
of
$u_\omega$
of
![]() $T$
are labelled bijectively by the elements
$T$
are labelled bijectively by the elements
![]() $\omega$
of the free monoid
$\omega$
of the free monoid
![]() $X^*$
in the following natural way: the root of
$X^*$
in the following natural way: the root of
![]() $T$
is labelled by the empty word and is denoted by
$T$
is labelled by the empty word and is denoted by
![]() $\epsilon$
, and for each word
$\epsilon$
, and for each word
![]() $\omega \in X^*$
and letter
$\omega \in X^*$
and letter
![]() $x \in X$
, there is an edge connecting
$x \in X$
, there is an edge connecting
![]() $u_\omega$
to
$u_\omega$
to
![]() $u_{\omega x}$
. More generally, we say that
$u_{\omega x}$
. More generally, we say that
![]() $u_\omega$
precedes
$u_\omega$
precedes
![]() $u_\lambda$
whenever
$u_\lambda$
whenever
![]() $\omega$
is a prefix of
$\omega$
is a prefix of
![]() $\lambda$
.
$\lambda$
.
There is a natural length function on
![]() $X^*$
, which is defined as follows: the words
$X^*$
, which is defined as follows: the words
![]() $\omega$
of length
$\omega$
of length
![]() $\lvert \omega \rvert = n$
, representing vertices
$\lvert \omega \rvert = n$
, representing vertices
![]() $u_\omega$
that are at distance
$u_\omega$
that are at distance
![]() $n$
from the root, are the
$n$
from the root, are the
![]() $n$
th level vertices and constitute the
$n$
th level vertices and constitute the
![]() $n$
th layer of the tree.
$n$
th layer of the tree.
We denote by
![]() $T_u$
the full rooted subtree of
$T_u$
the full rooted subtree of
![]() $T$
that has its root at a vertex
$T$
that has its root at a vertex
![]() $u$
and includes all vertices succeeding
$u$
and includes all vertices succeeding
![]() $u$
. For any two vertices
$u$
. For any two vertices
![]() $u = u_\omega$
and
$u = u_\omega$
and
![]() $v = u_\lambda$
, the map
$v = u_\lambda$
, the map
![]() $u_{\omega \tau } \mapsto u_{\lambda \tau }$
, induced by replacing the prefix
$u_{\omega \tau } \mapsto u_{\lambda \tau }$
, induced by replacing the prefix
![]() $\omega$
by
$\omega$
by
![]() $\lambda$
, yields an isomorphism between the subtrees
$\lambda$
, yields an isomorphism between the subtrees
![]() $T_u$
and
$T_u$
and
![]() $T_v$
.
$T_v$
.
Now each
![]() $f\in \textrm{Aut}\, T$
fixes the root, and the orbits of
$f\in \textrm{Aut}\, T$
fixes the root, and the orbits of
![]() $\textrm{Aut}\, T$
on the vertices of the tree
$\textrm{Aut}\, T$
on the vertices of the tree
![]() $T$
are the layers of the tree
$T$
are the layers of the tree
![]() $T$
. The image of a vertex
$T$
. The image of a vertex
![]() $u$
under
$u$
under
![]() $f$
will be denoted by
$f$
will be denoted by
![]() $uf$
. The automorphism
$uf$
. The automorphism
![]() $f$
induces a faithful action on
$f$
induces a faithful action on
![]() $X^*$
given by
$X^*$
given by
![]() $(u_\omega )f = u_{\omega f}$
. For
$(u_\omega )f = u_{\omega f}$
. For
![]() $\omega \in X^*$
and
$\omega \in X^*$
and
![]() $x \in X$
, we have
$x \in X$
, we have
![]() $(\omega x)f = (\omega f) x^{\prime}$
, for
$(\omega x)f = (\omega f) x^{\prime}$
, for
![]() $x^{\prime} \in X$
uniquely determined by
$x^{\prime} \in X$
uniquely determined by
![]() $\omega$
and
$\omega$
and
![]() $f$
. This induces a permutation
$f$
. This induces a permutation
![]() $f^\omega$
of
$f^\omega$
of
![]() $X$
which satisfies
$X$
which satisfies
More generally, for an automorphism
![]() $f$
of
$f$
of
![]() $T$
, since the layers are invariant under
$T$
, since the layers are invariant under
![]() $f$
, for
$f$
, for
![]() $u\in X^*$
, the equation
$u\in X^*$
, the equation
defines a unique automorphism
![]() $f_u$
of
$f_u$
of
![]() $T$
called the section of
$T$
called the section of
![]() $f$
at
$f$
at
![]() $u$
. This automorphism can be viewed as the automorphism of
$u$
. This automorphism can be viewed as the automorphism of
![]() $T$
induced by
$T$
induced by
![]() $f$
upon identifying the rooted subtrees of
$f$
upon identifying the rooted subtrees of
![]() $T$
at the vertices
$T$
at the vertices
![]() $u$
and
$u$
and
![]() $uf$
with the tree
$uf$
with the tree
![]() $T$
. As seen here, we often do not differentiate between
$T$
. As seen here, we often do not differentiate between
![]() $X^*$
and vertices of
$X^*$
and vertices of
![]() $T$
.
$T$
.
2.1. Subgroups of
 $\textrm{Aut}\, T$
$\textrm{Aut}\, T$
Let
![]() $G$
be a subgroup of
$G$
be a subgroup of
![]() $\textrm{Aut}\, T$
acting level-transitively, that is, transitively on every layer of
$\textrm{Aut}\, T$
acting level-transitively, that is, transitively on every layer of
![]() $T$
. The vertex stabiliser
$T$
. The vertex stabiliser
![]() $\textrm{st}_G(u)$
is the subgroup consisting of elements in
$\textrm{st}_G(u)$
is the subgroup consisting of elements in
![]() $G$
that fix the vertex
$G$
that fix the vertex
![]() $u$
. For
$u$
. For
![]() $n \in \mathbb{N}$
, the
$n \in \mathbb{N}$
, the
![]() $n$
th level stabiliser
$n$
th level stabiliser
![]() $\textrm{St}_G(n)= \bigcap _{\lvert \omega \rvert =n} \textrm{st}_G(u_\omega )$
is the subgroup consisting of automorphisms that fix all vertices at level
$\textrm{St}_G(n)= \bigcap _{\lvert \omega \rvert =n} \textrm{st}_G(u_\omega )$
is the subgroup consisting of automorphisms that fix all vertices at level
![]() $n$
.
$n$
.
Each
![]() $g\in \textrm{St}_{\textrm{Aut}\, T} (n)$
can be completely determined in terms of its restrictions to the subtrees rooted at vertices at level
$g\in \textrm{St}_{\textrm{Aut}\, T} (n)$
can be completely determined in terms of its restrictions to the subtrees rooted at vertices at level
![]() $n$
. There is a natural isomorphism
$n$
. There is a natural isomorphism
defined by sending
![]() $g\in \textrm{St}_{\textrm{Aut}\, T} (n)$
to its tuple of
$g\in \textrm{St}_{\textrm{Aut}\, T} (n)$
to its tuple of
![]() $m^n$
sections. For conciseness, we will omit the use of
$m^n$
sections. For conciseness, we will omit the use of
![]() $\psi _1$
, and simply write
$\psi _1$
, and simply write
![]() $g=(g_1,\ldots,g_m)$
for
$g=(g_1,\ldots,g_m)$
for
![]() $g\in \text{St}_{\textrm{Aut}\, T}(1)$
.
$g\in \text{St}_{\textrm{Aut}\, T}(1)$
.
Let
![]() $\omega \in X^n$
be of length
$\omega \in X^n$
be of length
![]() $n$
. We further define
$n$
. We further define
to be the map sending
![]() $f\in \textrm{st}_{\textrm{Aut}\, T}(u_\omega )$
to the section
$f\in \textrm{st}_{\textrm{Aut}\, T}(u_\omega )$
to the section
![]() $f_{u_\omega }$
.
$f_{u_\omega }$
.
A group
![]() $G \leq \textrm{Aut}\, T$
is said to be self-similar if for all
$G \leq \textrm{Aut}\, T$
is said to be self-similar if for all
![]() $f\in G$
and all
$f\in G$
and all
![]() $\omega \in X^*$
the section
$\omega \in X^*$
the section
![]() $f_{u_{\omega }}$
belongs to
$f_{u_{\omega }}$
belongs to
![]() $G$
. We will denote
$G$
. We will denote
![]() $G_{\omega }$
to be the subgroup
$G_{\omega }$
to be the subgroup
![]() $\varphi _{\omega }(\textrm{st}_G(u_{\omega }))$
.
$\varphi _{\omega }(\textrm{st}_G(u_{\omega }))$
.
Recall that for a group
![]() $G$
generated by a finite symmetric subset
$G$
generated by a finite symmetric subset
![]() $S$
(i.e. a set for which
$S$
(i.e. a set for which
![]() $S = S^{-1}$
), for every
$S = S^{-1}$
), for every
![]() $g \in G$
, the length of
$g \in G$
, the length of
![]() $g$
with respect to
$g$
with respect to
![]() $S$
is
$S$
is
Now assume that
![]() $G$
is a self-similar subgroup of
$G$
is a self-similar subgroup of
![]() $\textrm{Aut}\, T$
. Then for every
$\textrm{Aut}\, T$
. Then for every
![]() $g\in G$
and every
$g\in G$
and every
![]() $n\in \mathbb{N}_0\cup \{0\}$
, let
$n\in \mathbb{N}_0\cup \{0\}$
, let
If there exist
![]() $\lambda \lt 1$
and
$\lambda \lt 1$
and
![]() $C,L\in \mathbb{N}$
such that
$C,L\in \mathbb{N}$
such that
then we say that the group
![]() $G$
is contracting with respect to
$G$
is contracting with respect to
![]() $S$
.
$S$
.
Let
![]() $G$
be a subgroup of
$G$
be a subgroup of
![]() $\textrm{Aut}\, T$
acting level-transitively. Here, the vertex stabilisers at every level are conjugate under
$\textrm{Aut}\, T$
acting level-transitively. Here, the vertex stabilisers at every level are conjugate under
![]() $G$
. We say that the group
$G$
. We say that the group
![]() $G$
is fractal if
$G$
is fractal if
![]() $G_{\omega }\,{:\!=}\,\varphi _\omega (\textrm{st}_G(u_\omega ))=G$
for every
$G_{\omega }\,{:\!=}\,\varphi _\omega (\textrm{st}_G(u_\omega ))=G$
for every
![]() $\omega \in X^*$
, after the natural identification of subtrees. Furthermore, we say that the group
$\omega \in X^*$
, after the natural identification of subtrees. Furthermore, we say that the group
![]() $G$
is super strongly fractal if, for each
$G$
is super strongly fractal if, for each
![]() $n\in \mathbb{N}$
, we have
$n\in \mathbb{N}$
, we have
![]() $\varphi _\omega (\text{St}_G(n))=G$
for every word
$\varphi _\omega (\text{St}_G(n))=G$
for every word
![]() $\omega \in X^n$
of length
$\omega \in X^n$
of length
![]() $n$
.
$n$
.
The rigid vertex stabiliser of
![]() $u$
in
$u$
in
![]() $G$
is the subgroup
$G$
is the subgroup
![]() $\textrm{rist}_G(u)$
consisting of all automorphisms in
$\textrm{rist}_G(u)$
consisting of all automorphisms in
![]() $G$
that fix all vertices of
$G$
that fix all vertices of
![]() $T$
not succeeding
$T$
not succeeding
![]() $u$
. The rigid
$u$
. The rigid
![]() $n$
th level stabiliser is the direct product of the rigid vertex stabilisers of the vertices at level
$n$
th level stabiliser is the direct product of the rigid vertex stabilisers of the vertices at level
![]() $n$
:
$n$
:
We recall that a level-transitive group
![]() $G$
is a branch group if
$G$
is a branch group if
![]() $\textrm{Rist}_G(n)$
has finite index in
$\textrm{Rist}_G(n)$
has finite index in
![]() $G$
for every
$G$
for every
![]() $n \in \mathbb{N}$
; and
$n \in \mathbb{N}$
; and
![]() $G$
is weakly branch if
$G$
is weakly branch if
![]() $\textrm{Rist}_G(n)$
is non-trivial for every
$\textrm{Rist}_G(n)$
is non-trivial for every
![]() $n \in \mathbb{N}$
. If, in addition, the group
$n \in \mathbb{N}$
. If, in addition, the group
![]() $G$
is self-similar and there exists a subgroup
$G$
is self-similar and there exists a subgroup
![]() $1 \ne K \leq G$
with
$1 \ne K \leq G$
with
![]() $K\times \overset{m}\cdots \times K \subseteq{\psi _1}(\textrm{St}_K(1))$
and
$K\times \overset{m}\cdots \times K \subseteq{\psi _1}(\textrm{St}_K(1))$
and
![]() $\lvert G \,{:}\, K \rvert \lt \infty$
, then
$\lvert G \,{:}\, K \rvert \lt \infty$
, then
![]() $G$
is said to be regular branch over
$G$
is said to be regular branch over
![]() $K$
. If in the previous definition the condition
$K$
. If in the previous definition the condition
![]() $\lvert G\,{:}\, K \rvert \lt \infty$
is omitted, then
$\lvert G\,{:}\, K \rvert \lt \infty$
is omitted, then
![]() $G$
is said to be weakly regular branch over
$G$
is said to be weakly regular branch over
![]() $K$
.
$K$
.
2.2. A basic result
Here we record a general result that will be useful in the sequel. For
![]() $g\in \textrm{Aut}\, T$
, recall that
$g\in \textrm{Aut}\, T$
, recall that
![]() $g^\epsilon$
denotes the action induced by
$g^\epsilon$
denotes the action induced by
![]() $g$
at the root of
$g$
at the root of
![]() $T$
.
$T$
.
Lemma 2.1.
For a self-similar group
![]() $G\le \textrm{Aut}\, T$
, let
$G\le \textrm{Aut}\, T$
, let
![]() $z = (z_0,\dots,z_{m-1})z^\epsilon \in G^{\prime}$
. Then
$z = (z_0,\dots,z_{m-1})z^\epsilon \in G^{\prime}$
. Then
![]() $z_0\cdots z_{m-1}\in G^{\prime}$
.
$z_0\cdots z_{m-1}\in G^{\prime}$
.
Proof. It suffices to prove the result for a basic commutator
![]() $[g,h]$
, where
$[g,h]$
, where
![]() $g,h\in G$
. Write
$g,h\in G$
. Write
![]() $g=(g_0,\ldots,g_{m-1})g^\epsilon$
and
$g=(g_0,\ldots,g_{m-1})g^\epsilon$
and
![]() $h=(h_0,\ldots,h_{m-1})h^\epsilon$
. For notational convenience, let us write
$h=(h_0,\ldots,h_{m-1})h^\epsilon$
. For notational convenience, let us write
![]() $\tau =(g^\epsilon )^{-1}$
and
$\tau =(g^\epsilon )^{-1}$
and
![]() $\kappa =(h^\epsilon )^{-1}$
, and for
$\kappa =(h^\epsilon )^{-1}$
, and for
![]() $\alpha \in \text{Sym}(X)$
and
$\alpha \in \text{Sym}(X)$
and
![]() $x\in X$
we write
$x\in X$
we write
![]() $x^\alpha$
for the image
$x^\alpha$
for the image
![]() $\alpha (x)$
of
$\alpha (x)$
of
![]() $x$
under
$x$
under
![]() $\alpha$
. As
$\alpha$
. As
 \begin{align*} &[g,h]\\ &= \tau (g_0^{-1},\dots,g_{m-1}^{-1}) \kappa (h_0^{-1},\dots,h_{m-1}^{-1}) (g_0,\dots,g_{m-1})g^\epsilon (h_0,\dots,h_{m-1})h^\epsilon \\ & = (g_{0^\tau }^{-1},\dots,g_{(m-1)^\tau }^{-1}) (h_{0^{\tau \kappa }}^{-1},\dots,h_{(m-1)^{\tau \kappa }}^{-1}) (g_{0^{\tau \kappa }},\dots,g_{(m-1)^{\tau \kappa }})(h_{0^{\tau \kappa{g^\epsilon }}},\dots,h_{(m-1)^{\tau \kappa{g^\epsilon }}})\tau \kappa{g^\epsilon h^\epsilon }, \end{align*}
\begin{align*} &[g,h]\\ &= \tau (g_0^{-1},\dots,g_{m-1}^{-1}) \kappa (h_0^{-1},\dots,h_{m-1}^{-1}) (g_0,\dots,g_{m-1})g^\epsilon (h_0,\dots,h_{m-1})h^\epsilon \\ & = (g_{0^\tau }^{-1},\dots,g_{(m-1)^\tau }^{-1}) (h_{0^{\tau \kappa }}^{-1},\dots,h_{(m-1)^{\tau \kappa }}^{-1}) (g_{0^{\tau \kappa }},\dots,g_{(m-1)^{\tau \kappa }})(h_{0^{\tau \kappa{g^\epsilon }}},\dots,h_{(m-1)^{\tau \kappa{g^\epsilon }}})\tau \kappa{g^\epsilon h^\epsilon }, \end{align*}
the result follows.
3. Properties of
 $\mathfrak{K(v)}$
$\mathfrak{K(v)}$
For any two integers
![]() $i,j,$
let
$i,j,$
let
![]() $[i, j]$
denote the set
$[i, j]$
denote the set
![]() $\{i,i+1,\dots,j-1,j\}$
. In the following sections, we fix
$\{i,i+1,\dots,j-1,j\}$
. In the following sections, we fix
![]() $m,s\in \mathbb{N}_{\geq 2}$
. Let
$m,s\in \mathbb{N}_{\geq 2}$
. Let
![]() $X = \{0,1,\dots,m-1\}$
and let
$X = \{0,1,\dots,m-1\}$
and let
![]() ${\mathfrak{v}}= x_0\cdots x_{s-2}$
be a word in
${\mathfrak{v}}= x_0\cdots x_{s-2}$
be a word in
![]() $X^*$
. Recall that the group
$X^*$
. Recall that the group
![]() $\mathfrak{K(v)}$
is generated by the elements
$\mathfrak{K(v)}$
is generated by the elements
![]() $a_0,\dots,a_{s-1}$
, where
$a_0,\dots,a_{s-1}$
, where
for
![]() $i \in{[0, s-2]}.$
$i \in{[0, s-2]}.$
To prove Theorem 1.1(i), we use the following characterisation of iterated monodromy groups by Nekrashevych [Reference Nekrashevych21, Theorem 6.10.8] according to the notation given in [Reference Jones18, Theorem 5.8]:
Theorem 3.1.
A subgroup
![]() $G\le \text{Aut } T$
is isomorphic to a standard action of the iterated monodromy group of a post-critically finite polynomial if and only if
$G\le \text{Aut } T$
is isomorphic to a standard action of the iterated monodromy group of a post-critically finite polynomial if and only if
![]() $G$
is conjugate in
$G$
is conjugate in
![]() $\text{Aut }T$
to a group generated by a finite invertible automaton
$\text{Aut }T$
to a group generated by a finite invertible automaton
![]() $A$
with the following properties:
$A$
with the following properties:
-
(1) For each non-trivial
 $a\in A$
, there is a unique
$a\in A$
, there is a unique
 $b\in A$
and
$b\in A$
and
 $x\in X$
with
$x\in X$
with
 ${b_x}=a$
.
${b_x}=a$
. -
(2) For each
 $a\in A$
and each cycle
$a\in A$
and each cycle
 $(x_1\,x_2\,\cdots \,x_n)$
of the action of
$(x_1\,x_2\,\cdots \,x_n)$
of the action of
 $a$
on
$a$
on
 $X$
, the section
$X$
, the section
 $a_{x_i}$
is non-trivial for at most one
$a_{x_i}$
is non-trivial for at most one
 $x_i$
.
$x_i$
. -
(3) The multi-set of permutations defined by the set of states of
 $A$
acting on
$A$
acting on
 $X$
is tree-like.
$X$
is tree-like.
-
(4) Let
 $a_1\ne a_2$
be non-trivial states of
$a_1\ne a_2$
be non-trivial states of
 $A$
with
$A$
with
 $\epsilon \ne v_1,v_2\in T$
satisfying
$\epsilon \ne v_1,v_2\in T$
satisfying
 $(a_i)_{v_i}=a_i$
and
$(a_i)_{v_i}=a_i$
and
 $a_i(v_i)=v_i$
for
$a_i(v_i)=v_i$
for
 $i\in \{1,2\}$
. Then, there is no
$i\in \{1,2\}$
. Then, there is no
 $h\in G$
with
$h\in G$
with
 $h(v_1)=v_2$
and
$h(v_1)=v_2$
and
 $h_{v_1}=h$
.
$h_{v_1}=h$
.
We refer the reader to [Reference Nekrashevych21] or [Reference Jones18] for any unexplained terminology.
Proof of Theorem 1.1(i). We will show that the above four conditions hold for
![]() $\mathfrak{K(v)}$
. Conditions (1) and (2) of Theorem 3.1 are clear from the definition of the generators
$\mathfrak{K(v)}$
. Conditions (1) and (2) of Theorem 3.1 are clear from the definition of the generators
![]() $a_i$
. For condition (3), notice that
$a_i$
. For condition (3), notice that
![]() $a_0$
is the only generator of
$a_0$
is the only generator of
![]() $\mathfrak{K(v)}$
that acts non-trivially on
$\mathfrak{K(v)}$
that acts non-trivially on
![]() $X$
. Therefore, according to [Reference Jones18, Section 5.4], the multi-set of permutations of
$X$
. Therefore, according to [Reference Jones18, Section 5.4], the multi-set of permutations of
![]() $X$
is given by
$X$
is given by
![]() $\{\sigma \}$
. Furthermore, the cycle diagram associated with the multi-set
$\{\sigma \}$
. Furthermore, the cycle diagram associated with the multi-set
![]() $\{\sigma \}$
is an oriented 2-dimensional CW complex, whose set of 0-cells is
$\{\sigma \}$
is an oriented 2-dimensional CW complex, whose set of 0-cells is
![]() $X$
, and with one 2-cell obtained by connecting the elements of
$X$
, and with one 2-cell obtained by connecting the elements of
![]() $X$
by the action of
$X$
by the action of
![]() $\sigma$
. Hence, the cycle diagram is contractible. Thus, by [Reference Jones18, Definition 5.7] the multi-set of permutations defined by the set of states of
$\sigma$
. Hence, the cycle diagram is contractible. Thus, by [Reference Jones18, Definition 5.7] the multi-set of permutations defined by the set of states of
![]() $\mathfrak{K(v)}$
acting on
$\mathfrak{K(v)}$
acting on
![]() $X$
is tree-like.
$X$
is tree-like.
For condition (4), the restriction
![]() $(a_i)_{v_i}=a_i$
implies that the
$(a_i)_{v_i}=a_i$
implies that the
![]() $v_i$
have to be at level
$v_i$
have to be at level
![]() $ns$
for some positive integer
$ns$
for some positive integer
![]() $n$
. However, for any
$n$
. However, for any
![]() $a_i$
, after
$a_i$
, after
![]() $i$
levels, the section is
$i$
levels, the section is
![]() $a_0$
, which does not then fix any vertex below it. So we can never find vertices
$a_0$
, which does not then fix any vertex below it. So we can never find vertices
![]() $v_i$
such that
$v_i$
such that
![]() $a_i(v_i)=v_i$
. So (4) vacuously holds.
$a_i(v_i)=v_i$
. So (4) vacuously holds.
Lemma 3.2.
The group
![]() $\mathfrak{K(v)}$
is super strongly fractal and level-transitive.
$\mathfrak{K(v)}$
is super strongly fractal and level-transitive.
Proof. Observe that
![]() $a_0^m=(a_{s-1},\dots,a_{s-1})$
and, for any
$a_0^m=(a_{s-1},\dots,a_{s-1})$
and, for any
![]() $i \in{[1, s-1]}$
and
$i \in{[1, s-1]}$
and
![]() $j \in{[0, m-1]}$
,
$j \in{[0, m-1]}$
,
It follows that
![]() ${\varphi _x(\textrm{St}}_{\mathfrak{K(v)}}(1))=\mathfrak{K(v)}$
for all
${\varphi _x(\textrm{St}}_{\mathfrak{K(v)}}(1))=\mathfrak{K(v)}$
for all
![]() $x \in X$
. For
$x \in X$
. For
![]() $n\in \mathbb{N}$
, we write
$n\in \mathbb{N}$
, we write
![]() $n=\ell s+r$
, where
$n=\ell s+r$
, where
![]() $\ell \in \mathbb{N}_0$
and
$\ell \in \mathbb{N}_0$
and
![]() $r\in [0,s-1]$
. Using similar arguments with the elements
$r\in [0,s-1]$
. Using similar arguments with the elements
and their conjugates, we deduce that
![]() ${\varphi _w(\textrm{St}}_{\mathfrak{K(v)}}(n))=\mathfrak{K(v)}$
for all
${\varphi _w(\textrm{St}}_{\mathfrak{K(v)}}(n))=\mathfrak{K(v)}$
for all
![]() $w \in X^n$
.
$w \in X^n$
.
The second statement is immediate from the fact that
![]() ${\varphi _x(\textrm{st}}_{\mathfrak{K(v)}}(x))=\mathfrak{K(v)}$
for some
${\varphi _x(\textrm{st}}_{\mathfrak{K(v)}}(x))=\mathfrak{K(v)}$
for some
![]() $x \in X$
, and since
$x \in X$
, and since
![]() $a_0$
, and hence,
$a_0$
, and hence,
![]() $\mathfrak{K(v)}$
, acts transitively on the first layer.
$\mathfrak{K(v)}$
, acts transitively on the first layer.
Next, we record an elementary but useful result. Recall that
![]() ${\mathfrak{v}} = x_0\cdots x_{s-2}$
is a word in
${\mathfrak{v}} = x_0\cdots x_{s-2}$
is a word in
![]() $X^*$
.
$X^*$
.
Lemma 3.3.
For distinct
![]() $i,j\in [1,s-1]$
with
$i,j\in [1,s-1]$
with
![]() $x_{i-1}\ne x_{j-1}$
, we have
$x_{i-1}\ne x_{j-1}$
, we have
![]() $[a_i,a_j]=1$
in
$[a_i,a_j]=1$
in
![]() $\mathfrak{K(v)}$
. For
$\mathfrak{K(v)}$
. For
![]() $i\gt \ell \in [1, s-1]$
with
$i\gt \ell \in [1, s-1]$
with
![]() $x_{i-1}= x_{\ell -1}$
, we have
$x_{i-1}= x_{\ell -1}$
, we have
![]() $[a_i,a_\ell ]=1$
if
$[a_i,a_\ell ]=1$
if
![]() $x_{i-d}\ne x_{\ell -d}$
for some
$x_{i-d}\ne x_{\ell -d}$
for some
![]() $d\in [2,\ell ]$
and
$d\in [2,\ell ]$
and
![]() $[a_i,a_\ell ]\ne 1$
otherwise.
$[a_i,a_\ell ]\ne 1$
otherwise.
Proof. The first statement is a straightforward computation. For the next statement, note that for
![]() $i\in [1,s-1]$
,
$i\in [1,s-1]$
,
 \begin{equation*} [a_i,a_0]=\begin {cases} (a_{s-1}^{-1}a_{i-1}a_{s-1},1,\ldots,1,a_{i-1}^{-1})&\text {if }x_{i-1}= m-1,\\ (1,\overset {x_{i-1}-1}\ldots,1,a_{i-1}^{-1},a_{i-1},1,\ldots,1)&\text {if }x_{i-1}\ne m-1, \end {cases} \end{equation*}
\begin{equation*} [a_i,a_0]=\begin {cases} (a_{s-1}^{-1}a_{i-1}a_{s-1},1,\ldots,1,a_{i-1}^{-1})&\text {if }x_{i-1}= m-1,\\ (1,\overset {x_{i-1}-1}\ldots,1,a_{i-1}^{-1},a_{i-1},1,\ldots,1)&\text {if }x_{i-1}\ne m-1, \end {cases} \end{equation*}
so
![]() $a_0$
does not commute with any other
$a_0$
does not commute with any other
![]() $a_i$
. The result then follows, using the fact that
$a_i$
. The result then follows, using the fact that
Lemma 3.4.
The group
![]() $\mathfrak{K(v)}$
is weakly regular branch over
$\mathfrak{K(v)}$
is weakly regular branch over
![]() $\mathfrak{K(v)}^{\prime}$
.
$\mathfrak{K(v)}^{\prime}$
.
Proof. We use that
![]() $\mathfrak{K(v)}^{\prime} = \langle [a_i,a_j] \mid i,j \in{[0, s-1]}\rangle ^{\mathfrak{K(v)}}$
. We have
$\mathfrak{K(v)}^{\prime} = \langle [a_i,a_j] \mid i,j \in{[0, s-1]}\rangle ^{\mathfrak{K(v)}}$
. We have
 \begin{align*} \Big [a_i^{a_0^{m-1-x_{i-1}}}, a_j^{a_0^{m-1-x_{j-1}}}\Big ] &= (1,\dots,1,[a_{i-1},a_{j-1}]),\\ [a_i, a_0^m]^{a_0^{m-1-x_{i-1}}} &= (1,\dots,1,[a_{i-1}, a_{s-1}]), \end{align*}
\begin{align*} \Big [a_i^{a_0^{m-1-x_{i-1}}}, a_j^{a_0^{m-1-x_{j-1}}}\Big ] &= (1,\dots,1,[a_{i-1},a_{j-1}]),\\ [a_i, a_0^m]^{a_0^{m-1-x_{i-1}}} &= (1,\dots,1,[a_{i-1}, a_{s-1}]), \end{align*}
for
![]() $i,j\in{[1, s-1]}.$
Therefore, by transitivity and fractalness, we have
$i,j\in{[1, s-1]}.$
Therefore, by transitivity and fractalness, we have
![]() $\mathfrak{K(v)}^{\prime} \times \overset{m}\cdots \times \mathfrak{K(v)}^{\prime} \leq \psi (\mathfrak{K(v)}^{\prime})$
.
$\mathfrak{K(v)}^{\prime} \times \overset{m}\cdots \times \mathfrak{K(v)}^{\prime} \leq \psi (\mathfrak{K(v)}^{\prime})$
.
For
![]() $i \in{[0, s-1]}$
, let
$i \in{[0, s-1]}$
, let
![]() $A_i = \langle a_j\mid{j\in [0,s-1]\backslash \{i\}} \rangle ^{\mathfrak{K(v)}}$
.
$A_i = \langle a_j\mid{j\in [0,s-1]\backslash \{i\}} \rangle ^{\mathfrak{K(v)}}$
.
Lemma 3.5.
For
![]() $i \in{[0, s-1]}$
, we have
$i \in{[0, s-1]}$
, we have
![]() $\mathfrak{K(v)}/A_i \cong \mathbb{Z}$
. In particular, the elements
$\mathfrak{K(v)}/A_i \cong \mathbb{Z}$
. In particular, the elements
![]() $a_i$
have infinite order in
$a_i$
have infinite order in
![]() $\mathfrak{K(v)}$
.
$\mathfrak{K(v)}$
.
Proof. We prove simultaneously for all
![]() $i$
that
$i$
that
![]() $\mathfrak{K(v)}/A_i \cong \mathbb{Z}.$
Assume for a contradiction that, for some
$\mathfrak{K(v)}/A_i \cong \mathbb{Z}.$
Assume for a contradiction that, for some
![]() $n \in \mathbb{N}$
that
$n \in \mathbb{N}$
that
![]() $a_i^n \in A_i$
, for some
$a_i^n \in A_i$
, for some
![]() $i \in{[0, s-1]}.$
Choose
$i \in{[0, s-1]}.$
Choose
![]() $n \in \mathbb{N}$
minimal with respect to the property that
$n \in \mathbb{N}$
minimal with respect to the property that
![]() $a_i^n \in A_i$
for some
$a_i^n \in A_i$
for some
![]() $i \in{[0, s-1]}$
. If
$i \in{[0, s-1]}$
. If
![]() $i =0$
, then
$i =0$
, then
![]() $a_{0}^n \in \textrm{St}_{\mathfrak{K(v)}}(1)$
and, in particular
$a_{0}^n \in \textrm{St}_{\mathfrak{K(v)}}(1)$
and, in particular
![]() $n \equiv 0{\pmod m}$
. We have
$n \equiv 0{\pmod m}$
. We have
and hence,
![]() $a_{s-1}^{{n}/{m}} \in A_{s-1}.$
This is a contradiction to the minimality of
$a_{s-1}^{{n}/{m}} \in A_{s-1}.$
This is a contradiction to the minimality of
![]() $n$
. Now suppose that
$n$
. Now suppose that
![]() $i \neq 0$
. Then by considering appropriate sections of
$i \neq 0$
. Then by considering appropriate sections of
![]() $a_i^n$
, we see that
$a_i^n$
, we see that
![]() $a_0^n \in A_0$
, which cannot happen as shown above. Therefore, we conclude that
$a_0^n \in A_0$
, which cannot happen as shown above. Therefore, we conclude that
![]() ${\mathfrak{K(v)}}/A_i \cong \mathbb{Z}$
for all
${\mathfrak{K(v)}}/A_i \cong \mathbb{Z}$
for all
![]() $i \in{[0, s-1]}$
.
$i \in{[0, s-1]}$
.
Lemma 3.6.
We have
![]() $\textrm{Rist}_{\mathfrak{K(v)}}(1)=A_0$
. Hence, the group
$\textrm{Rist}_{\mathfrak{K(v)}}(1)=A_0$
. Hence, the group
![]() $\mathfrak{K(v)}$
is not branch.
$\mathfrak{K(v)}$
is not branch.
Proof. Analogous to the proof of [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Theorem 3.5(i)], we clearly have
![]() $A_0\le \textrm{Rist}_{\mathfrak{K(v)}}(1)\le \textrm{St}_{\mathfrak{K(v)}}(1)=A_0\langle a_0^m \rangle$
, where the last equality follows from the fact that
$A_0\le \textrm{Rist}_{\mathfrak{K(v)}}(1)\le \textrm{St}_{\mathfrak{K(v)}}(1)=A_0\langle a_0^m \rangle$
, where the last equality follows from the fact that
![]() $a_i\in \textrm{St}_{\mathfrak{K(v)}}(1)$
for all
$a_i\in \textrm{St}_{\mathfrak{K(v)}}(1)$
for all
![]() $i\ne 0$
, and that
$i\ne 0$
, and that
![]() $a_0^n\in \textrm{St}_{ \mathfrak{K(v)}}(1)$
if and only if
$a_0^n\in \textrm{St}_{ \mathfrak{K(v)}}(1)$
if and only if
![]() $n\equiv 0\pmod m$
. So
$n\equiv 0\pmod m$
. So
![]() $\textrm{Rist}_{\mathfrak{K(v)}}(1)=A_0\langle a_0^{mn} \rangle$
for some
$\textrm{Rist}_{\mathfrak{K(v)}}(1)=A_0\langle a_0^{mn} \rangle$
for some
![]() $n$
. Since
$n$
. Since
and
![]() $a_{s-1}$
has infinite order modulo
$a_{s-1}$
has infinite order modulo
![]() $A_{s-1}$
by Lemma 3.5, it follows from the definition of the rigid stabiliser that
$A_{s-1}$
by Lemma 3.5, it follows from the definition of the rigid stabiliser that
![]() $n=0$
. Hence,
$n=0$
. Hence,
![]() $\textrm{Rist}_{\mathfrak{K(v)}}(1)=A_0$
, which has infinite index in
$\textrm{Rist}_{\mathfrak{K(v)}}(1)=A_0$
, which has infinite index in
![]() $\mathfrak{K(v)}$
, so
$\mathfrak{K(v)}$
, so
![]() $\mathfrak{K(v)}$
is not branch.
$\mathfrak{K(v)}$
is not branch.
We shall adopt the convention that the subscripts of the
![]() $a_i$
’s are taken modulo
$a_i$
’s are taken modulo
![]() $s$
. Set
$s$
. Set
![]() $S = \{a_i^{\pm 1} \mid i \in{[0, s-1]}\}$
and then
$S = \{a_i^{\pm 1} \mid i \in{[0, s-1]}\}$
and then
![]() $\mathfrak{K(v)}= \langle S \rangle$
. For each word
$\mathfrak{K(v)}= \langle S \rangle$
. For each word
![]() $w \in S^*$
, the length
$w \in S^*$
, the length
![]() $|w|$
is the usual word length of
$|w|$
is the usual word length of
![]() $w$
over the alphabet
$w$
over the alphabet
![]() $S$
.
$S$
.
Lemma 3.7.
Let
![]() $w$
be a word in
$w$
be a word in
![]() $S$
representing the identity in
$S$
representing the identity in
![]() $\mathfrak{K(v)}$
. Then the exponent sum of
$\mathfrak{K(v)}$
. Then the exponent sum of
![]() $a_i$
in
$a_i$
in
![]() $w$
must be zero for all
$w$
must be zero for all
![]() $i \in{[0, s-1]}$
.
$i \in{[0, s-1]}$
.
Proof. We proceed by induction on the length of
![]() $w$
. Let
$w$
. Let
![]() $w$
be a non-trivial word in
$w$
be a non-trivial word in
![]() $S$
representing the identity in
$S$
representing the identity in
![]() $\mathfrak{K(v)}$
. It is immediate from Lemma 3.5 that
$\mathfrak{K(v)}$
. It is immediate from Lemma 3.5 that
![]() $|w| \geq 2$
and
$|w| \geq 2$
and
![]() $w$
must contain non-trivial powers of at least two distinct
$w$
must contain non-trivial powers of at least two distinct
![]() $a_i,a_j \in S$
. For the base case
$a_i,a_j \in S$
. For the base case
![]() $|w|=2$
, we have that
$|w|=2$
, we have that
![]() $w=a_i^{\epsilon _i}a_j^{\epsilon _j}$
for distinct
$w=a_i^{\epsilon _i}a_j^{\epsilon _j}$
for distinct
![]() $i,j\in [0,s-1]$
and
$i,j\in [0,s-1]$
and
![]() $\epsilon _i,\epsilon _j\in \{\pm 1\}$
. From considering the image of
$\epsilon _i,\epsilon _j\in \{\pm 1\}$
. From considering the image of
![]() $w$
in
$w$
in
![]() $\mathfrak{K(v)}/A_i$
, we obtain a contradiction to
$\mathfrak{K(v)}/A_i$
, we obtain a contradiction to
![]() $\epsilon _i$
being non-zero.
$\epsilon _i$
being non-zero.
Assume that the result holds for all words of length
![]() $n \geq 2$
, and let
$n \geq 2$
, and let
![]() $|w|=n+1$
. By realising
$|w|=n+1$
. By realising
![]() $w$
in
$w$
in
![]() $\mathfrak{K(v)}$
, we can see that the exponent sum of
$\mathfrak{K(v)}$
, we can see that the exponent sum of
![]() $a_0$
in
$a_0$
in
![]() $w$
must be zero modulo
$w$
must be zero modulo
![]() $m$
. By abuse of notation, we write
$m$
. By abuse of notation, we write
where
![]() $w_i$
are reduced words determined by the appropriate sections of the letters of
$w_i$
are reduced words determined by the appropriate sections of the letters of
![]() $w$
. Since
$w$
. Since
![]() $w$
represents the identity in
$w$
represents the identity in
![]() $\mathfrak{K(v)}$
, each
$\mathfrak{K(v)}$
, each
![]() $w_k$
also represents the identity in
$w_k$
also represents the identity in
![]() $\mathfrak{K(v)}$
. It follows from the definition of the generators
$\mathfrak{K(v)}$
. It follows from the definition of the generators
![]() $a_i$
that
$a_i$
that
![]() $\sum \limits _{k=0}^{m-1}|w_{k}| \leq |w|$
. In particular, if
$\sum \limits _{k=0}^{m-1}|w_{k}| \leq |w|$
. In particular, if
![]() $|w_{k}| = |w|$
, for some
$|w_{k}| = |w|$
, for some
![]() $k \in{[0, m-1]}$
, then the
$k \in{[0, m-1]}$
, then the
![]() $w_j$
are trivial for all
$w_j$
are trivial for all
![]() $j \in{[0, m-1]}\backslash \{k\}$
, otherwise
$j \in{[0, m-1]}\backslash \{k\}$
, otherwise
![]() $|w_{k}| \lt |w|$
for all
$|w_{k}| \lt |w|$
for all
![]() ${k} \in{[0, m-1]}$
.
${k} \in{[0, m-1]}$
.
Assume that
![]() $|w_{k}| \lt |w|$
for all
$|w_{k}| \lt |w|$
for all
![]() $k \in{[0, m-1]}$
. By the induction hypothesis, for all
$k \in{[0, m-1]}$
. By the induction hypothesis, for all
![]() $i \in{[0, s-1]}$
the exponent sum of
$i \in{[0, s-1]}$
the exponent sum of
![]() $a_i$
is zero in
$a_i$
is zero in
![]() $w_{k}$
for all
$w_{k}$
for all
![]() ${k} \in{[0, m-1]}$
. Since the
${k} \in{[0, m-1]}$
. Since the
![]() $a_i$
in
$a_i$
in
![]() $w_{k}$
are obtained from
$w_{k}$
are obtained from
![]() $a_{i+1}$
in
$a_{i+1}$
in
![]() $w$
, we conclude that the exponent sum of
$w$
, we conclude that the exponent sum of
![]() $a_{i+1}$
in
$a_{i+1}$
in
![]() $w$
is zero for all
$w$
is zero for all
![]() $i \in{[0, s-1]}$
.
$i \in{[0, s-1]}$
.
Now, assume that there exists
![]() $k \in{[0, m-1]}$
such that
$k \in{[0, m-1]}$
such that
![]() $|w_k| = |w|$
. By replacing
$|w_k| = |w|$
. By replacing
![]() $w$
with
$w$
with
![]() $w_k$
, repeatedly if necessary, we may assume that
$w_k$
, repeatedly if necessary, we may assume that
![]() $w$
does involve the letters
$w$
does involve the letters
![]() $a_0^{\pm 1}$
. Then, if
$a_0^{\pm 1}$
. Then, if
![]() $w$
has
$w$
has
![]() $a_0^{\pm 1}$
as a letter, then the total exponent of
$a_0^{\pm 1}$
as a letter, then the total exponent of
![]() $a_0$
is congruent to 0 modulo
$a_0$
is congruent to 0 modulo
![]() $m$
. Suppose first that the total exponent of
$m$
. Suppose first that the total exponent of
![]() $a_0$
is non-zero. Since the total exponent of
$a_0$
is non-zero. Since the total exponent of
![]() $a_0$
is congruent to
$a_0$
is congruent to
![]() $0$
modulo
$0$
modulo
![]() $m$
, we can find a subword
$m$
, we can find a subword
![]() $a_0^{\pm 1}w^{\prime} a_0^{\pm 1}$
such that the exponent sum of
$a_0^{\pm 1}w^{\prime} a_0^{\pm 1}$
such that the exponent sum of
![]() $a_0$
in
$a_0$
in
![]() $w^{\prime}$
is zero. By realising this subword in
$w^{\prime}$
is zero. By realising this subword in
![]() $\mathfrak{K(v)}$
, we immediately see a length reduction among the sections, and it follows by induction that every section
$\mathfrak{K(v)}$
, we immediately see a length reduction among the sections, and it follows by induction that every section
![]() $w_k$
has exponent sum of
$w_k$
has exponent sum of
![]() $a_i$
equal to zero for all
$a_i$
equal to zero for all
![]() $i\in [0,s-1]$
. So in particular, the case that total exponent of
$i\in [0,s-1]$
. So in particular, the case that total exponent of
![]() $a_0$
in
$a_0$
in
![]() $w$
is non-zero cannot occur. So assume that the total exponent of
$w$
is non-zero cannot occur. So assume that the total exponent of
![]() $a_0$
is zero. Upon considering each
$a_0$
is zero. Upon considering each
![]() $w_k$
, we may assume that the total exponent of
$w_k$
, we may assume that the total exponent of
![]() $a_0$
in
$a_0$
in
![]() $w_k$
is zero, else we are done by the above argument. Hence, the total exponent of
$w_k$
is zero, else we are done by the above argument. Hence, the total exponent of
![]() $a_1$
in
$a_1$
in
![]() $w$
is zero. Recursively, we deduce that the total exponent in
$w$
is zero. Recursively, we deduce that the total exponent in
![]() $w$
of any
$w$
of any
![]() $a_i$
is zero. The result then follows.
$a_i$
is zero. The result then follows.
We proceed to prove parts (iv) and (v) of Theorem 1.1.
Lemma 3.8.
The quotient group
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}$
is isomorphic to the free abelian group of rank
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}$
is isomorphic to the free abelian group of rank
![]() $s$
.
$s$
.
Proof. For every
![]() $g \in \mathfrak{K(v)}$
, there exist integers
$g \in \mathfrak{K(v)}$
, there exist integers
![]() $n_0,\dots,n_{s-1}$
such that
$n_0,\dots,n_{s-1}$
such that
![]() $g \equiv a_0^{n_0}\cdots a_{s-1}^{n_{s-1}}$
modulo
$g \equiv a_0^{n_0}\cdots a_{s-1}^{n_{s-1}}$
modulo
![]() $\mathfrak{K(v)}^{\prime}$
. It is enough to show that, if
$\mathfrak{K(v)}^{\prime}$
. It is enough to show that, if
![]() $a_0^{n_0}\cdots a_{s-1}^{n_{s-1}} \in \mathfrak{K(v)}^{\prime}$
, for some
$a_0^{n_0}\cdots a_{s-1}^{n_{s-1}} \in \mathfrak{K(v)}^{\prime}$
, for some
![]() $n_0,\dots,n_{s-1} \in \mathbb{Z}$
, then
$n_0,\dots,n_{s-1} \in \mathbb{Z}$
, then
![]() $n_0=\cdots =n_{s-1} = 0$
.
$n_0=\cdots =n_{s-1} = 0$
.
Assume that
![]() $a_0^{n_0}\cdots a_{s-1}^{n_{s-1}} \in \mathfrak{K(v)}^{\prime}$
for some
$a_0^{n_0}\cdots a_{s-1}^{n_{s-1}} \in \mathfrak{K(v)}^{\prime}$
for some
![]() $n_0,\dots,n_{s-1} \in \mathbb{Z}$
. It is clear that every element in
$n_0,\dots,n_{s-1} \in \mathbb{Z}$
. It is clear that every element in
![]() $\mathfrak{K(v)}^{\prime}$
can be written as a word in
$\mathfrak{K(v)}^{\prime}$
can be written as a word in
![]() $S$
and the exponent sum of each
$S$
and the exponent sum of each
![]() $a_i$
is zero. It follows from Lemma 3.7 that the exponent sums of the
$a_i$
is zero. It follows from Lemma 3.7 that the exponent sums of the
![]() $a_i$
’s in all words representing the same element in
$a_i$
’s in all words representing the same element in
![]() $\mathfrak{K(v)}$
are the same. This, in particular, applies to
$\mathfrak{K(v)}$
are the same. This, in particular, applies to
![]() $a_0^{n_0}\cdots a_{s-1}^{n_{s-1}}$
, and hence,
$a_0^{n_0}\cdots a_{s-1}^{n_{s-1}}$
, and hence,
![]() $n_0 = \cdots = n_{s-1} = 0$
.
$n_0 = \cdots = n_{s-1} = 0$
.
Lemma 3.9.
The group
![]() $\mathfrak{K(v)}$
is torsion-free.
$\mathfrak{K(v)}$
is torsion-free.
Proof. It follows immediately from [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Theorem 3.6] that
![]() $\mathfrak{K(v)}$
is torsion-free as the quotient group
$\mathfrak{K(v)}$
is torsion-free as the quotient group
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}$
is torsion-free and the subgroup
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}$
is torsion-free and the subgroup
![]() $\mathfrak{K(v)}^{\prime}$
is contained in
$\mathfrak{K(v)}^{\prime}$
is contained in
![]() $\textrm{St}_{\mathfrak{K(v)}}(1)$
.
$\textrm{St}_{\mathfrak{K(v)}}(1)$
.
Next, we finish the proof of Theorem 1.1. Recall that for
![]() $g\in \mathfrak{K(v)}$
, the
$g\in \mathfrak{K(v)}$
, the
![]() $n$
th level sections
$n$
th level sections
![]() $g_0,\ldots,g_{m^n-1}$
of
$g_0,\ldots,g_{m^n-1}$
of
![]() $g$
are determined from expressing
$g$
are determined from expressing
![]() $g$
as the product
$g$
as the product
where
![]() $\psi _n^{-1}((g_0,\ldots,g_{m^n-1}))\in \textrm{St}_{\mathfrak{K(v)}}(n)$
and
$\psi _n^{-1}((g_0,\ldots,g_{m^n-1}))\in \textrm{St}_{\mathfrak{K(v)}}(n)$
and
![]() $\tau _g\in \textrm{Sym}(X^n)$
.
$\tau _g\in \textrm{Sym}(X^n)$
.
Theorem 3.10.
The group
![]() $\mathfrak{K(v)}$
is contracting with respect to the set of generators
$\mathfrak{K(v)}$
is contracting with respect to the set of generators
![]() $S$
, with
$S$
, with
![]() $\lambda =\frac{2}{3}$
,
$\lambda =\frac{2}{3}$
,
![]() $L=s-1$
and
$L=s-1$
and
![]() $C=1$
.
$C=1$
.
Proof. By [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Lemma 3.7], it suffices to prove that
We can further reduce the problem to showing that
![]() $\ell _s(h)\le 2$
for every
$\ell _s(h)\le 2$
for every
![]() $h\in \mathfrak{K(v)}$
of length
$h\in \mathfrak{K(v)}$
of length
![]() $3$
. Indeed, writing
$3$
. Indeed, writing
![]() $|g|=3\alpha +\beta$
with
$|g|=3\alpha +\beta$
with
![]() $\beta \in \{0,1,2\}$
and
$\beta \in \{0,1,2\}$
and
![]() $g=h_1\cdots h_\alpha f$
with
$g=h_1\cdots h_\alpha f$
with
![]() $|h_1|=\cdots =|h_\alpha |=3$
and
$|h_1|=\cdots =|h_\alpha |=3$
and
![]() $|f|=\beta$
, we see that (3.1) immediately follows from the subadditivity of
$|f|=\beta$
, we see that (3.1) immediately follows from the subadditivity of
![]() $\ell _s$
; cf. [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Equation (3.3)].
$\ell _s$
; cf. [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Equation (3.3)].
Let us then consider an arbitrary element
![]() $h\in \mathfrak{K(v)}$
of length
$h\in \mathfrak{K(v)}$
of length
![]() $3$
and prove that
$3$
and prove that
![]() $\ell _s(h)\le 2$
. Observe that
$\ell _s(h)\le 2$
. Observe that
![]() $h$
is of the form
$h$
is of the form
-
(i)
 $a_i^{\epsilon _i}a_j^{\epsilon _j}a_k^{\epsilon _k}$
for
$a_i^{\epsilon _i}a_j^{\epsilon _j}a_k^{\epsilon _k}$
for
 $i\ne j$
and
$i\ne j$
and
 $j\ne k$
; or
$j\ne k$
; or -
(ii)
 $a_i^{2\epsilon _i}a_j^{\epsilon _j}$
or
$a_i^{2\epsilon _i}a_j^{\epsilon _j}$
or
 $a_i^{\epsilon _i}a_j^{2\epsilon _j}$
for
$a_i^{\epsilon _i}a_j^{2\epsilon _j}$
for
 $i\ne j$
; or
$i\ne j$
; or -
(iii)
 $a_i^{3\epsilon _i}$
,
$a_i^{3\epsilon _i}$
,
where
![]() $\epsilon _i, \epsilon _j, \epsilon _k\in \{\pm 1\}$
. For case (iii), it is clear that
$\epsilon _i, \epsilon _j, \epsilon _k\in \{\pm 1\}$
. For case (iii), it is clear that
![]() $\ell _{i+1}(h)\le 2$
, since the only non-trivial
$\ell _{i+1}(h)\le 2$
, since the only non-trivial
![]() $i$
th level section is
$i$
th level section is
![]() $a_0^{3\epsilon _i}$
. Similarly for case (ii).
$a_0^{3\epsilon _i}$
. Similarly for case (ii).
For case (i), suppose for a contradiction that
![]() $\ell _n(h)=3$
for all
$\ell _n(h)=3$
for all
![]() $n\in \mathbb{N}$
. Then note that for every
$n\in \mathbb{N}$
. Then note that for every
![]() $n$
, the element
$n$
, the element
![]() $h$
has exactly one non-trivial
$h$
has exactly one non-trivial
![]() $n$
th level section, which is
$n$
th level section, which is
![]() $a_{i-n}^{\epsilon _i}a_{j-n}^{\epsilon _j}a_{k-n}^{\epsilon _k}$
. As usual, the indices of the generators are viewed modulo
$a_{i-n}^{\epsilon _i}a_{j-n}^{\epsilon _j}a_{k-n}^{\epsilon _k}$
. As usual, the indices of the generators are viewed modulo
![]() $s$
, so we effectively only consider the first
$s$
, so we effectively only consider the first
![]() $(s-1)$
st level sections.
$(s-1)$
st level sections.
Consider now the non-trivial
![]() $i$
th level section, which is
$i$
th level section, which is
![]() $a_0^{\epsilon _i}a_{j-i}^{\epsilon _j}a_{k-i}^{\epsilon _k}$
. Suppose
$a_0^{\epsilon _i}a_{j-i}^{\epsilon _j}a_{k-i}^{\epsilon _k}$
. Suppose
![]() $k=i$
. If
$k=i$
. If
![]() $\epsilon _i=\epsilon _k$
, then clearly the
$\epsilon _i=\epsilon _k$
, then clearly the
![]() $(i+1)$
st sections decrease in length. So suppose
$(i+1)$
st sections decrease in length. So suppose
![]() $\epsilon _i\ne \epsilon _k$
. Upon considering the only non-trivial
$\epsilon _i\ne \epsilon _k$
. Upon considering the only non-trivial
![]() $j$
th level section
$j$
th level section
![]() $a_{i-j}^{\epsilon _i}a_{0}^{\epsilon _j}a_{i-j}^{\epsilon _k}$
, we see that
$a_{i-j}^{\epsilon _i}a_{0}^{\epsilon _j}a_{i-j}^{\epsilon _k}$
, we see that
![]() $\ell _{j+1}(h)\le 2$
. So we suppose that
$\ell _{j+1}(h)\le 2$
. So we suppose that
![]() $k\ne i$
. Consider first the case
$k\ne i$
. Consider first the case
![]() $\epsilon _i=1$
. Recall that the non-trivial
$\epsilon _i=1$
. Recall that the non-trivial
![]() $i$
th level section of
$i$
th level section of
![]() $h$
is
$h$
is
![]() $a_0a_{j-i}^{\epsilon _j}a_{k-i}^{\epsilon _k}$
. In order for
$a_0a_{j-i}^{\epsilon _j}a_{k-i}^{\epsilon _k}$
. In order for
![]() $\ell _{i+1}(h)$
to still be 3, we need
$\ell _{i+1}(h)$
to still be 3, we need
If the defining word
![]() $\mathfrak{v}$
of the group
$\mathfrak{v}$
of the group
![]() $\mathfrak{K(v)}$
does not correspond to the above generators, then this implies that our assumption for this case (i) does not hold, and hence, the section lengths eventually decrease, giving us
$\mathfrak{K(v)}$
does not correspond to the above generators, then this implies that our assumption for this case (i) does not hold, and hence, the section lengths eventually decrease, giving us
![]() $\ell _s(h)\le 2$
. So we proceed by assuming that
$\ell _s(h)\le 2$
. So we proceed by assuming that
![]() $\mathfrak{v}$
tallies with the above generators and with the other generators singled out below.
$\mathfrak{v}$
tallies with the above generators and with the other generators singled out below.
Next, we similarly see that in order for
![]() $\ell _{s+2i-j}(h)$
to still be 3, we need
$\ell _{s+2i-j}(h)$
to still be 3, we need
![]() $a_{j-i}a_{2j-2i}^{\epsilon _j}a_{j+k-2i}^{\epsilon _k}$
to have exactly one non-trivial section. Thus,
$a_{j-i}a_{2j-2i}^{\epsilon _j}a_{j+k-2i}^{\epsilon _k}$
to have exactly one non-trivial section. Thus,
In particular, proceeding in this manner, we may assume that
for all
![]() $\theta \in \mathbb{N}$
. Now let
$\theta \in \mathbb{N}$
. Now let
![]() $\theta =s-1$
, and so
$\theta =s-1$
, and so
![]() $a_{i-j}=(a_{i-j-1},1,\ldots,1)$
. Observe that the only non-trivial
$a_{i-j}=(a_{i-j-1},1,\ldots,1)$
. Observe that the only non-trivial
![]() $j$
th level section of
$j$
th level section of
![]() $h$
is
$h$
is
![]() $a_{i-j}a_0^{\epsilon _j}a_{k-j}^{\epsilon _k}$
. To avoid a decrease in length at the next level, we must have
$a_{i-j}a_0^{\epsilon _j}a_{k-j}^{\epsilon _k}$
. To avoid a decrease in length at the next level, we must have
![]() $\epsilon _j=-1$
and
$\epsilon _j=-1$
and
![]() $a_{k-j}=(1,\ldots,1,a_{k-j-1})$
. Similarly, for
$a_{k-j}=(1,\ldots,1,a_{k-j-1})$
. Similarly, for
![]() $\ell _{s+2j-k}(h)$
to still be 3, we need
$\ell _{s+2j-k}(h)$
to still be 3, we need
![]() $a_{k-2j+i}a_{k-j}^{-1}a_{2(k-j)}^{\epsilon _k}$
to have exactly one non-trivial section. Thus,
$a_{k-2j+i}a_{k-j}^{-1}a_{2(k-j)}^{\epsilon _k}$
to have exactly one non-trivial section. Thus,
As deduced above, since
![]() $a_{k-i}=(a_{k-i-1},1,\ldots,1)$
we also then have that
$a_{k-i}=(a_{k-i-1},1,\ldots,1)$
we also then have that
for all
![]() $\theta \in \mathbb{N}$
. As before, we let
$\theta \in \mathbb{N}$
. As before, we let
![]() $\theta =s-1$
, and consider the only non-trivial
$\theta =s-1$
, and consider the only non-trivial
![]() $k$
th level section of
$k$
th level section of
![]() $h$
, which is
$h$
, which is
![]() $a_{i-k}a_{j-k}^{-1}a_{0}^{\epsilon _k}$
. Since
$a_{i-k}a_{j-k}^{-1}a_{0}^{\epsilon _k}$
. Since
Then, we see that
![]() $\ell _{k+1}(h)\le 2$
, and we are done in this case
$\ell _{k+1}(h)\le 2$
, and we are done in this case
![]() $\epsilon _i=1$
.
$\epsilon _i=1$
.
The remaining case
![]() $\epsilon _i=-1$
follows similarly. Hence, the proof is complete.
$\epsilon _i=-1$
follows similarly. Hence, the proof is complete.
Lemma 3.11.
The semigroup generated by
![]() $a_0,\dots,a_{s-1}$
is free. In particular, the group
$a_0,\dots,a_{s-1}$
is free. In particular, the group
![]() $\mathfrak{K(v)}$
has exponential word growth.
$\mathfrak{K(v)}$
has exponential word growth.
Proof. We proceed as in the proof of [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Theorem 6.1], which is based on [Reference Grigorchuk and Żuk15, Lemma 4]. Let
![]() $u$
and
$u$
and
![]() $w$
be two different words representing the same element in the semigroup generated by
$w$
be two different words representing the same element in the semigroup generated by
![]() $a_0,\dots,a_{s-1}$
, and with
$a_0,\dots,a_{s-1}$
, and with
![]() $\rho =\max (|u|,|w|)$
minimal. Clearly,
$\rho =\max (|u|,|w|)$
minimal. Clearly,
![]() $\rho \ge 2$
. Now for any word
$\rho \ge 2$
. Now for any word
![]() $z$
in the semigroup, let
$z$
in the semigroup, let
![]() $|z|_{a_0}$
denote the
$|z|_{a_0}$
denote the
![]() $a_0$
-length in
$a_0$
-length in
![]() $z$
, that is, the number of occurrences of
$z$
, that is, the number of occurrences of
![]() $a_0$
in
$a_0$
in
![]() $z$
. Note that we have
$z$
. Note that we have
![]() $|u|_{a_0}\equiv |w|_{a_0} \pmod m$
. In the rest of the proof, we may consider the sections of
$|u|_{a_0}\equiv |w|_{a_0} \pmod m$
. In the rest of the proof, we may consider the sections of
![]() $u$
and
$u$
and
![]() $w$
as defined in the proof of Lemma 3.7.
$w$
as defined in the proof of Lemma 3.7.
Suppose first that
![]() $u$
contains no
$u$
contains no
![]() $a_0$
s. We may assume that
$a_0$
s. We may assume that
![]() $w$
contains at least one
$w$
contains at least one
![]() $a_0$
. Indeed, if both
$a_0$
. Indeed, if both
![]() $u$
and
$u$
and
![]() $w$
have no
$w$
have no
![]() $a_0$
’s, by replacing both words with their corresponding non-trivial sections respectively, the condition of both words having no
$a_0$
’s, by replacing both words with their corresponding non-trivial sections respectively, the condition of both words having no
![]() $a_0$
’s cannot hold indefinitely, as then both words
$a_0$
’s cannot hold indefinitely, as then both words
![]() $u$
and
$u$
and
![]() $w$
would be the trivial word. Thus
$w$
would be the trivial word. Thus
![]() $w$
contains at least one
$w$
contains at least one
![]() $a_0$
. Since
$a_0$
. Since
![]() $|w|_{a_0}$
must then be a non-zero multiple of
$|w|_{a_0}$
must then be a non-zero multiple of
![]() $m$
, one deduces that
$m$
, one deduces that
![]() $w_j$
, for
$w_j$
, for
![]() $j\in [0,m-1]$
, is a non-empty word, where
$j\in [0,m-1]$
, is a non-empty word, where
![]() $\psi (w)=(w_0,\ldots,w_{m-1})$
. Indeed, every component of
$\psi (w)=(w_0,\ldots,w_{m-1})$
. Indeed, every component of
![]() $\psi (w)$
contains an
$\psi (w)$
contains an
![]() $a_{s-1}$
. Certainly
$a_{s-1}$
. Certainly
![]() $|w_j|\lt \rho$
. Therefore,
$|w_j|\lt \rho$
. Therefore,
![]() $u$
must have only one section with a non-empty word, as otherwise, it will contradict the minimality of
$u$
must have only one section with a non-empty word, as otherwise, it will contradict the minimality of
![]() $\rho$
. Suppose this section is in the
$\rho$
. Suppose this section is in the
![]() $i$
th component, for some
$i$
th component, for some
![]() $i\in [0,m-1]$
. From considering the
$i\in [0,m-1]$
. From considering the
![]() $j$
th section of
$j$
th section of
![]() $u$
and
$u$
and
![]() $w$
, for
$w$
, for
![]() $j\ne i$
, we obtain a contradiction to the minimality of
$j\ne i$
, we obtain a contradiction to the minimality of
![]() $\rho$
. So the number of occurrences of
$\rho$
. So the number of occurrences of
![]() $a_0$
in
$a_0$
in
![]() $u$
is at least one.
$u$
is at least one.
If the number of occurrences of
![]() $a_0$
in
$a_0$
in
![]() $u$
, respectively
$u$
, respectively
![]() $w$
, is at least 2, then there are at least two sections of
$w$
, is at least 2, then there are at least two sections of
![]() $u$
, respectively
$u$
, respectively
![]() $w$
, that contain
$w$
, that contain
![]() $a_{s-1}$
. Hence, all sections of
$a_{s-1}$
. Hence, all sections of
![]() $u$
, respectively
$u$
, respectively
![]() $w$
, have length strictly less than
$w$
, have length strictly less than
![]() $|u|$
, respectively
$|u|$
, respectively
![]() $|w|$
, which contradicts the minimality of
$|w|$
, which contradicts the minimality of
![]() $\rho$
. So suppose that both
$\rho$
. So suppose that both
![]() $u$
and
$u$
and
![]() $w$
have exactly one occurrence of
$w$
have exactly one occurrence of
![]() $a_0$
. Repeating this argument for the sections of
$a_0$
. Repeating this argument for the sections of
![]() $u$
and
$u$
and
![]() $w$
, we may assume that every generator appears at most once in
$w$
, we may assume that every generator appears at most once in
![]() $u$
and
$u$
and
![]() $w$
and that the same generators appear in both
$w$
and that the same generators appear in both
![]() $u$
and
$u$
and
![]() $w$
. In other words, the word
$w$
. In other words, the word
![]() $w$
is a reordering of the letters in
$w$
is a reordering of the letters in
![]() $u$
. Furthermore, as seen above, both
$u$
. Furthermore, as seen above, both
![]() $u$
and
$u$
and
![]() $w$
have only one non-empty section, which is therefore the rightmost section. Indeed, if this is not the case, then either
$w$
have only one non-empty section, which is therefore the rightmost section. Indeed, if this is not the case, then either
![]() $u$
or
$u$
or
![]() $w$
have more than one non-trivial section, then we contradict the minimality of
$w$
have more than one non-trivial section, then we contradict the minimality of
![]() $\rho$
. Without loss of generality, we may suppose that
$\rho$
. Without loss of generality, we may suppose that
![]() $a_0$
is the
$a_0$
is the
![]() $i$
th letter of the word
$i$
th letter of the word
![]() $u$
, but the
$u$
, but the
![]() $j$
th letter of the word
$j$
th letter of the word
![]() $w$
where
$w$
where
![]() $j\lt i$
. The restrictions on the sections of
$j\lt i$
. The restrictions on the sections of
![]() $u$
imply that the first
$u$
imply that the first
![]() $i$
letters of
$i$
letters of
![]() $u$
have non-empty section in the rightmost component, and all other letters have non-empty section in the leftmost component. At least one of these first
$u$
have non-empty section in the rightmost component, and all other letters have non-empty section in the leftmost component. At least one of these first
![]() $i-1$
letters of
$i-1$
letters of
![]() $u$
appears to the right of
$u$
appears to the right of
![]() $a_0$
in the word
$a_0$
in the word
![]() $w$
. Thus, there is a non-empty section in the second last component, which yields a contradiction to the minimality of
$w$
. Thus, there is a non-empty section in the second last component, which yields a contradiction to the minimality of
![]() $\rho$
. Hence, we are done.
$\rho$
. Hence, we are done.
Lastly, we end this section with a result that will be useful for the final section.
Lemma 3.12.
The subgroup
![]() $\psi ^{-1}(\gamma _3(\mathfrak{K(v)}) \times \overset{m}\cdots \times \gamma _3(\mathfrak{K(v)}))$
is contained in
$\psi ^{-1}(\gamma _3(\mathfrak{K(v)}) \times \overset{m}\cdots \times \gamma _3(\mathfrak{K(v)}))$
is contained in
![]() $\mathfrak{K(v)}^{\prime\prime}$
.
$\mathfrak{K(v)}^{\prime\prime}$
.
Proof. Notice first that, for
![]() $i \in{[1, s-1]}$
with
$i \in{[1, s-1]}$
with
![]() $x_{i-1} \neq m-1$
, we have
$x_{i-1} \neq m-1$
, we have
When
![]() $x_{i-1} = m-1$
, we get
$x_{i-1} = m-1$
, we get
Together with Lemma 3.4, we see that the elements of the form
are contained in
![]() $\psi (\mathfrak{K(v)}^{\prime\prime})$
, for
$\psi (\mathfrak{K(v)}^{\prime\prime})$
, for
![]() $i,j \in{[0, s-1]}$
and
$i,j \in{[0, s-1]}$
and
![]() $k \in{[0, s-2]}$
.
$k \in{[0, s-2]}$
.
We have to find the elements of the form
![]() $(1,\dots,1,{[a_i,a_j,a_{s-1}]} )$
. Observe from Lemma 3.4 that
$(1,\dots,1,{[a_i,a_j,a_{s-1}]} )$
. Observe from Lemma 3.4 that
Then from the Hall-Witt identity, we deduce that
 \begin{align*} 1&=[a_j,a_i^{-1},a_{s-1}]^{a_i} [a_i,a_{s-1}^{-1},a_j]^{a_{s-1}}[a_{s-1},a_j^{-1},a_i]^{a_j}\\ &=[a_i,a_j,a_{s-1}^{a_i}] [a_{s-1},a_i,a_j^{a_{s-1}}][a_j,a_{s-1},a_i^{a_j}]\\ &\equiv [a_i,a_j,a_{s-1}] [a_{s-1},a_i,a_j][a_j,a_{s-1},a_i] \pmod{\mathfrak{K(v)}^{\prime\prime}}. \end{align*}
\begin{align*} 1&=[a_j,a_i^{-1},a_{s-1}]^{a_i} [a_i,a_{s-1}^{-1},a_j]^{a_{s-1}}[a_{s-1},a_j^{-1},a_i]^{a_j}\\ &=[a_i,a_j,a_{s-1}^{a_i}] [a_{s-1},a_i,a_j^{a_{s-1}}][a_j,a_{s-1},a_i^{a_j}]\\ &\equiv [a_i,a_j,a_{s-1}] [a_{s-1},a_i,a_j][a_j,a_{s-1},a_i] \pmod{\mathfrak{K(v)}^{\prime\prime}}. \end{align*}
Hence, if
![]() $i,j\ne s-1$
, from considering the product of
$i,j\ne s-1$
, from considering the product of
together with an appropriate element from
![]() $\mathfrak{K(v)}^{\prime\prime}\times \overset{m}{\cdots }\times \mathfrak{K(v)}^{\prime\prime}$
, we obtain
$\mathfrak{K(v)}^{\prime\prime}\times \overset{m}{\cdots }\times \mathfrak{K(v)}^{\prime\prime}$
, we obtain
If
![]() $i=s-1$
but
$i=s-1$
but
![]() $j\ne s-1$
, we will show that
$j\ne s-1$
, we will show that
![]() ${[a_{s-1},a_j},a_{s-1}]=1$
. To this end, in light of Lemma 3.3 it suffices to consider
${[a_{s-1},a_j},a_{s-1}]=1$
. To this end, in light of Lemma 3.3 it suffices to consider
![]() ${[a_{s-1-j},a_0},a_{s-1-j}]$
. Recall from the proof of Lemma 3.3 that
${[a_{s-1-j},a_0},a_{s-1-j}]$
. Recall from the proof of Lemma 3.3 that
 \begin{equation*} [a_{s-1-j},a_0]=\begin {cases} (a_{s-1}^{-1}a_{s-j-2}a_{s-1},1,\ldots,1,a_{s-j-2}^{-1})&\text {if }x_{s-j-2}= m-1,\\ (1,\overset {x_{s-j-2}-1}\ldots,1,a_{s-j-2}^{-1},a_{s-j-2},1,\ldots,1)&\text {if }x_{s-j-2}\ne m-1. \end {cases} \end{equation*}
\begin{equation*} [a_{s-1-j},a_0]=\begin {cases} (a_{s-1}^{-1}a_{s-j-2}a_{s-1},1,\ldots,1,a_{s-j-2}^{-1})&\text {if }x_{s-j-2}= m-1,\\ (1,\overset {x_{s-j-2}-1}\ldots,1,a_{s-j-2}^{-1},a_{s-j-2},1,\ldots,1)&\text {if }x_{s-j-2}\ne m-1. \end {cases} \end{equation*}
Hence, it is now clear that
![]() ${[a_{s-1-j},a_0},a_{s-1-j}]=1$
.
${[a_{s-1-j},a_0},a_{s-1-j}]=1$
.
If
![]() $j=s-1$
but
$j=s-1$
but
![]() $i\ne s-1$
, from the Hall-Witt identity, we have the equivalence
$i\ne s-1$
, from the Hall-Witt identity, we have the equivalence
Hence, we are done from the previous case.
The result now follows from the level-transitivity and the fractalness of
![]() $\mathfrak{K(v)}$
.
$\mathfrak{K(v)}$
.
4. Length-reducing properties
As before, we have
![]() ${\mathfrak{v}} = x_0 \cdots x_{s-2}$
is a word in the alphabet
${\mathfrak{v}} = x_0 \cdots x_{s-2}$
is a word in the alphabet
![]() $X=\{0,1,\dots,m-1\}$
and
$X=\{0,1,\dots,m-1\}$
and
![]() $\mathfrak{K(v)}$
is the group associated with
$\mathfrak{K(v)}$
is the group associated with
![]() $\mathfrak{v}$
. In this section, we establish some length-reducing properties for some of the groups
$\mathfrak{v}$
. In this section, we establish some length-reducing properties for some of the groups
![]() $\mathfrak{K(v)}$
. Notice that for every
$\mathfrak{K(v)}$
. Notice that for every
![]() $g \in \mathfrak{K(v)}$
, the local action
$g \in \mathfrak{K(v)}$
, the local action
![]() $g^{\epsilon }$
of
$g^{\epsilon }$
of
![]() $g$
at the root is an element of
$g$
at the root is an element of
![]() $\langle \sigma \rangle$
. Hence, for conciseness, we denote
$\langle \sigma \rangle$
. Hence, for conciseness, we denote
![]() $g^{\epsilon }$
by
$g^{\epsilon }$
by
![]() $\sigma _g$
. If
$\sigma _g$
. If
![]() $g \in \mathfrak{K(v)}$
then
$g \in \mathfrak{K(v)}$
then
![]() $|g|$
denotes the minimal length of all words in the alphabet
$|g|$
denotes the minimal length of all words in the alphabet
![]() $S$
representing
$S$
representing
![]() $g$
. A word
$g$
. A word
![]() $w \in S^*$
is called a geodesic word if
$w \in S^*$
is called a geodesic word if
![]() $\vert w \vert = \vert g \vert$
, where
$\vert w \vert = \vert g \vert$
, where
![]() $g$
is the image of the word
$g$
is the image of the word
![]() $w$
in
$w$
in
![]() $\mathfrak{K(v)}$
.
$\mathfrak{K(v)}$
.
Lemma 4.1.
Let
![]() $g = (g_0,\dots,g_{m-1})\sigma _g \in \mathfrak{K(v)}.$
Then
$g = (g_0,\dots,g_{m-1})\sigma _g \in \mathfrak{K(v)}.$
Then
![]() $\sum \limits _{k =0}^{m-1} \vert g_k \vert \leq \vert g \vert$
.
$\sum \limits _{k =0}^{m-1} \vert g_k \vert \leq \vert g \vert$
.
Proof. The proof proceeds by induction on the length of
![]() $g$
. Clearly, the result is true if
$g$
. Clearly, the result is true if
![]() $\vert g \vert =0$
and
$\vert g \vert =0$
and
![]() $\vert g \vert =1.$
Assume that
$\vert g \vert =1.$
Assume that
![]() $\vert g \vert \gt 1.$
Let
$\vert g \vert \gt 1.$
Let
![]() $w \in S^*$
be a geodesic word representing
$w \in S^*$
be a geodesic word representing
![]() $g$
. The word
$g$
. The word
![]() $w$
can be written as
$w$
can be written as
![]() $w=bw^{\prime}$
for some
$w=bw^{\prime}$
for some
![]() $b \in S$
and
$b \in S$
and
![]() $w^{\prime}\in S^*$
such that
$w^{\prime}\in S^*$
such that
![]() $w^{\prime}$
is reduced. Then
$w^{\prime}$
is reduced. Then
![]() $\vert w^{\prime} \vert \lt \vert w \vert$
and
$\vert w^{\prime} \vert \lt \vert w \vert$
and
![]() $w^{\prime}$
does not represent
$w^{\prime}$
does not represent
![]() $g$
in
$g$
in
![]() $\mathfrak{K(v)}$
. Denote by
$\mathfrak{K(v)}$
. Denote by
![]() $g^{\prime}$
the corresponding element in
$g^{\prime}$
the corresponding element in
![]() $\mathfrak{K(v)}$
. Then
$\mathfrak{K(v)}$
. Then
![]() $\vert g^{\prime} \vert \leq \vert w^{\prime} \vert \lt \vert w \vert = \vert g \vert$
. We obtain
$\vert g^{\prime} \vert \leq \vert w^{\prime} \vert \lt \vert w \vert = \vert g \vert$
. We obtain
which implies
![]() $g_k ={b}_kg^{\prime}_{k^{\sigma _{b}}}$
for all
$g_k ={b}_kg^{\prime}_{k^{\sigma _{b}}}$
for all
![]() $k \in{[0, m-1]}$
. It follows by induction that
$k \in{[0, m-1]}$
. It follows by induction that
Lemma 4.2.
Let
![]() ${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
![]() $X$
, and let
$X$
, and let
![]() $g = (g_0,\dots,g_{m-1})\sigma _g \in \mathfrak{K(v)}$
with
$g = (g_0,\dots,g_{m-1})\sigma _g \in \mathfrak{K(v)}$
with
![]() $\sigma _g = \sigma ^{i}$
for some
$\sigma _g = \sigma ^{i}$
for some
![]() $i \in{[1, m-1]}$
such that
$i \in{[1, m-1]}$
such that
![]() $\gcd{(i,m)}=1$
. Let
$\gcd{(i,m)}=1$
. Let
![]() $\alpha _0,\dots,\alpha _{m-1} \in \mathfrak{K(v)}$
be such that
$\alpha _0,\dots,\alpha _{m-1} \in \mathfrak{K(v)}$
be such that
![]() $g^m = (\alpha _0,\dots,\alpha _{m-1})$
. Then
$g^m = (\alpha _0,\dots,\alpha _{m-1})$
. Then
![]() $\vert \alpha _k \vert \leq \sum \limits _{\ell =0}^{m-1} \vert g_{\ell } \vert \leq \vert g \vert$
for all
$\vert \alpha _k \vert \leq \sum \limits _{\ell =0}^{m-1} \vert g_{\ell } \vert \leq \vert g \vert$
for all
![]() $k \in{[0, m-1]}$
.
$k \in{[0, m-1]}$
.
Proof. Observe that
By setting
![]() $\alpha _k = g_{k}g_{k^{\sigma ^i}}\cdots g_{k^{\sigma ^{(m-1)i}}}$
, for each
$\alpha _k = g_{k}g_{k^{\sigma ^i}}\cdots g_{k^{\sigma ^{(m-1)i}}}$
, for each
![]() $k \in{[0, m-1]}$
, we obtain
$k \in{[0, m-1]}$
, we obtain
where the last inequality follows from Lemma 4.1.
Lemma 4.3.
Let
![]() ${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
![]() $X\backslash \{0\}$
. Let
$X\backslash \{0\}$
. Let
![]() $g = (g_0,\dots,g_{m-1})\sigma _g \in{\mathfrak{K(v)}}$
and let
$g = (g_0,\dots,g_{m-1})\sigma _g \in{\mathfrak{K(v)}}$
and let
![]() ${b}_1 \cdots{b}_\ell \in S^*$
be a geodesic word representing
${b}_1 \cdots{b}_\ell \in S^*$
be a geodesic word representing
![]() $g$
. If there exist
$g$
. If there exist
![]() $1 \leq r \lt r^{\prime} \leq \ell$
such that
$1 \leq r \lt r^{\prime} \leq \ell$
such that
![]() ${b}_r = a_{0}$
,
${b}_r = a_{0}$
,
![]() ${b}_{r^{\prime}}=a_0^{-1}$
, then
${b}_{r^{\prime}}=a_0^{-1}$
, then
![]() $\sum \limits _{k =0}^{m-1} \vert g_k \vert \lt \vert g \vert .$
$\sum \limits _{k =0}^{m-1} \vert g_k \vert \lt \vert g \vert .$
Proof. By assumption, the word
![]() ${b}_1\cdots{b}_\ell$
contains a subword of the form
${b}_1\cdots{b}_\ell$
contains a subword of the form
![]() $a_{0}wa_{0}^{-1}$
, where
$a_{0}wa_{0}^{-1}$
, where
![]() $w$
is a non-trivial reduced word in the alphabet
$w$
is a non-trivial reduced word in the alphabet
![]() $S$
. We assume, without loss of generality, that
$S$
. We assume, without loss of generality, that
![]() $w$
is a reduced word in the alphabet
$w$
is a reduced word in the alphabet
![]() $S\setminus \{a_0^{\,\pm 1}\}$
. Let
$S\setminus \{a_0^{\,\pm 1}\}$
. Let
![]() $w$
represent an element
$w$
represent an element
![]() $h$
in
$h$
in
![]() $\mathfrak{K(v)}$
. Since
$\mathfrak{K(v)}$
. Since
![]() ${b}_1 \cdots{b}_\ell \in S^*$
is a geodesic word, the word
${b}_1 \cdots{b}_\ell \in S^*$
is a geodesic word, the word
![]() $w$
is also geodesic and so
$w$
is also geodesic and so
![]() $|h| = |w|$
. Notice that
$|h| = |w|$
. Notice that
![]() $\vert a_{0}w a_{0}^{-1} \vert = \vert w \vert + 2$
. Realising the word
$\vert a_{0}w a_{0}^{-1} \vert = \vert w \vert + 2$
. Realising the word
![]() $a_{0}wa_{0}^{-1}$
in
$a_{0}wa_{0}^{-1}$
in
![]() $\mathfrak{K(v)}$
gives
$\mathfrak{K(v)}$
gives
indeed, recall that by assumption we have
By Lemma 4.1, we get
![]() $\sum _{i=1}^{m-1}|\varphi _{i}(h)| \le |h| = |w|$
. Therefore, we conclude that
$\sum _{i=1}^{m-1}|\varphi _{i}(h)| \le |h| = |w|$
. Therefore, we conclude that
Lemma 4.4.
Let
![]() ${\mathfrak{v}} = 0 \,\overset{s-1}\dots \, 0$
and let
${\mathfrak{v}} = 0 \,\overset{s-1}\dots \, 0$
and let
![]() $g = (g_0,\dots,g_{m-1})\sigma ^{\epsilon } \in{\mathfrak{K(v)}}$
with
$g = (g_0,\dots,g_{m-1})\sigma ^{\epsilon } \in{\mathfrak{K(v)}}$
with
![]() $\epsilon \in \{\pm 1\}$
. Suppose
$\epsilon \in \{\pm 1\}$
. Suppose
![]() ${b}_1 \cdots{b}_\ell \in S^*$
is a geodesic word representing
${b}_1 \cdots{b}_\ell \in S^*$
is a geodesic word representing
![]() $g$
. If there exist
$g$
. If there exist
![]() $1 \leq r \lt r^{\prime} \leq \ell$
such that either
$1 \leq r \lt r^{\prime} \leq \ell$
such that either
![]() ${b}_r = a_{0}$
,
${b}_r = a_{0}$
,
![]() ${b}_{r^{\prime}}=a_0^{-1}$
or
${b}_{r^{\prime}}=a_0^{-1}$
or
![]() ${b}_r = a_{0}^{-1}$
,
${b}_r = a_{0}^{-1}$
,
![]() ${b}_{r^{\prime}}=a_0$
, then
${b}_{r^{\prime}}=a_0$
, then
![]() $\vert g_0g_1\cdots g_{m-1} \vert \lt \vert g \vert$
if
$\vert g_0g_1\cdots g_{m-1} \vert \lt \vert g \vert$
if
![]() $\epsilon =1$
, and
$\epsilon =1$
, and
![]() $\vert g_0g_{m-1}\cdots g_{1} \vert \lt \vert g \vert$
if
$\vert g_0g_{m-1}\cdots g_{1} \vert \lt \vert g \vert$
if
![]() $\epsilon =-1$
.
$\epsilon =-1$
.
Proof. Note that we may assume that there are no
![]() $1\le i\lt j\le \ell$
such that
$1\le i\lt j\le \ell$
such that
![]() $b_i=a_0^{-1}$
and
$b_i=a_0^{-1}$
and
![]() $b_j=a_0$
, as then the desired length reduction is clear. It then follows that
$b_j=a_0$
, as then the desired length reduction is clear. It then follows that
and
for some
![]() $\lambda \in \mathbb{N}_0$
and the
$\lambda \in \mathbb{N}_0$
and the
![]() $*\in \langle a_1,\ldots,a_{s-1}\rangle$
are arbitrary.
$*\in \langle a_1,\ldots,a_{s-1}\rangle$
are arbitrary.
Let
Write
![]() $w^{\prime}=(w_0^{\prime},\ldots,w_{m-1}^{\prime})$
and
$w^{\prime}=(w_0^{\prime},\ldots,w_{m-1}^{\prime})$
and
![]() $\lambda =\mu m+\chi$
for some
$\lambda =\mu m+\chi$
for some
![]() $\mu \in \mathbb{N}_0$
and
$\mu \in \mathbb{N}_0$
and
![]() $\chi \in [0,m-1]$
. If
$\chi \in [0,m-1]$
. If
![]() $\mu \ne 0$
, the first-level sections of
$\mu \ne 0$
, the first-level sections of
![]() $w^{\prime}$
have the following form
$w^{\prime}$
have the following form
 \begin{align*} w_0^{\prime} &=\varphi _0(*)(a_{s-1}\varphi _0(*))\overset{\mu -1}{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu -1}{\cdots }(\varphi _0(*)a_{s-1}^{-1}) \varphi _0(*)\\ w_1^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu -1}{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu -1}{\cdots }(\varphi _0(*)a_{s-1}^{-1})\\ &\,\,\,\vdots \\ w_{m-1-\chi }^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu -1}{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu -1}{\cdots }(\varphi _0(*)a_{s-1}^{-1})\\ w_{m-\chi }^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu }{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu }{\cdots }(\varphi _0(*)a_{s-1}^{-1})\\ &\,\,\,\vdots \\ w_{m-1}^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu }{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu }{\cdots }(\varphi _0(*)a_{s-1}^{-1}). \end{align*}
\begin{align*} w_0^{\prime} &=\varphi _0(*)(a_{s-1}\varphi _0(*))\overset{\mu -1}{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu -1}{\cdots }(\varphi _0(*)a_{s-1}^{-1}) \varphi _0(*)\\ w_1^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu -1}{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu -1}{\cdots }(\varphi _0(*)a_{s-1}^{-1})\\ &\,\,\,\vdots \\ w_{m-1-\chi }^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu -1}{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu -1}{\cdots }(\varphi _0(*)a_{s-1}^{-1})\\ w_{m-\chi }^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu }{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu }{\cdots }(\varphi _0(*)a_{s-1}^{-1})\\ &\,\,\,\vdots \\ w_{m-1}^{\prime}&=(a_{s-1}\varphi _0(*))\overset{\mu }{\cdots }(a_{s-1}\varphi _0(*))a_{s-1}\varphi _0(*)a_{s-1}^{-1} (\varphi _0(*)a_{s-1}^{-1})\overset{\mu }{\cdots }(\varphi _0(*)a_{s-1}^{-1}). \end{align*}
When
![]() $\mu = 0$
and hence
$\mu = 0$
and hence
![]() $\chi \ne 0$
, we get
$\chi \ne 0$
, we get
 \begin{align*} w_0^{\prime} &= \varphi _0(*)\\ w_1^{\prime} &= 1\\ &\,\,\,\vdots \\ w_{m-1-\chi }^{\prime} &= 1 \\ w_{m-\chi }^{\prime} &= a_{s-1}\varphi _0(*)a_{s-1}^{-1}\\ &\,\,\,\vdots \\ w_{m-1}^{\prime} &= a_{s-1}\varphi _0(*)a_{s-1}^{-1}. \end{align*}
\begin{align*} w_0^{\prime} &= \varphi _0(*)\\ w_1^{\prime} &= 1\\ &\,\,\,\vdots \\ w_{m-1-\chi }^{\prime} &= 1 \\ w_{m-\chi }^{\prime} &= a_{s-1}\varphi _0(*)a_{s-1}^{-1}\\ &\,\,\,\vdots \\ w_{m-1}^{\prime} &= a_{s-1}\varphi _0(*)a_{s-1}^{-1}. \end{align*}
Hence, a straightforward computation shows that
![]() $|g_0g_1\cdots g_{m-1}|\lt |g|$
if
$|g_0g_1\cdots g_{m-1}|\lt |g|$
if
![]() $\epsilon =1$
, and that
$\epsilon =1$
, and that
![]() $\vert g_0g_{m-1}\cdots g_{1} \vert \lt \vert g \vert$
if
$\vert g_0g_{m-1}\cdots g_{1} \vert \lt \vert g \vert$
if
![]() $\epsilon =-1$
, as required.
$\epsilon =-1$
, as required.
5. Maximal subgroups
It follows from Proposition 5.1 below together with [Reference Francoeur10, Proposition 2.21] that the group
![]() $\mathfrak{K(v)}$
admits maximal subgroups of infinite index if and only if it admits a proper subgroup
$\mathfrak{K(v)}$
admits maximal subgroups of infinite index if and only if it admits a proper subgroup
![]() $H \lt \mathfrak{K(v)}$
such that
$H \lt \mathfrak{K(v)}$
such that
![]() $HN = \mathfrak{K(v)}$
for every non-trivial normal subgroup
$HN = \mathfrak{K(v)}$
for every non-trivial normal subgroup
![]() $N \trianglelefteq \mathfrak{K(v)}$
. A subgroup
$N \trianglelefteq \mathfrak{K(v)}$
. A subgroup
![]() $H \leq \mathfrak{K(v)}$
satisfying the above condition is called a prodense subgroup. As seen below, we prove that
$H \leq \mathfrak{K(v)}$
satisfying the above condition is called a prodense subgroup. As seen below, we prove that
![]() $\mathfrak{K(v)}$
, for a constant word
$\mathfrak{K(v)}$
, for a constant word
![]() $\mathfrak{v}$
, does not admit any proper prodense subgroup, which proves Theorem 1.2.
$\mathfrak{v}$
, does not admit any proper prodense subgroup, which proves Theorem 1.2.
Proposition 5.1.
The group
![]() $\mathfrak{K(v)}$
is just non-(virtually nilpotent). Hence, maximal subgroups of proper quotients of
$\mathfrak{K(v)}$
is just non-(virtually nilpotent). Hence, maximal subgroups of proper quotients of
![]() $\mathfrak{K(v)}$
are of finite index.
$\mathfrak{K(v)}$
are of finite index.
Proof. As
![]() $\mathfrak{K(v)}$
has exponential word growth from Lemma 3.11, it follows from Bass [Reference Bass5] and Guivarc’h [Reference Guivarc’h16] that
$\mathfrak{K(v)}$
has exponential word growth from Lemma 3.11, it follows from Bass [Reference Bass5] and Guivarc’h [Reference Guivarc’h16] that
![]() $\mathfrak{K(v)}$
is not virtually nilpotent. To see that every proper quotient of
$\mathfrak{K(v)}$
is not virtually nilpotent. To see that every proper quotient of
![]() $\mathfrak{K(v)}$
is virtually nilpotent, by [Reference Francoeur10, Theorem 4.10], it suffices to prove that
$\mathfrak{K(v)}$
is virtually nilpotent, by [Reference Francoeur10, Theorem 4.10], it suffices to prove that
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime\prime}$
is virtually nilpotent. Set
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime\prime}$
is virtually nilpotent. Set
![]() $N = \psi ^{-1}(\gamma _3(\mathfrak{K(v)}) \times \cdots \times \gamma _3(\mathfrak{K(v)}))$
. From Lemma 3.12, we have
$N = \psi ^{-1}(\gamma _3(\mathfrak{K(v)}) \times \cdots \times \gamma _3(\mathfrak{K(v)}))$
. From Lemma 3.12, we have
![]() $N \leq \mathfrak{K(v)}^{\prime\prime} \lt \textrm{St}_{\mathfrak{K(v)}}(1) \lt{\mathfrak{K(v)}}$
. Therefore,
$N \leq \mathfrak{K(v)}^{\prime\prime} \lt \textrm{St}_{\mathfrak{K(v)}}(1) \lt{\mathfrak{K(v)}}$
. Therefore,
![]() $\psi$
induces a homomorphism
$\psi$
induces a homomorphism
Since
![]() $\widetilde{\psi }$
is injective and
$\widetilde{\psi }$
is injective and
![]() $\widetilde{\psi }(\textrm{St}_{\mathfrak{K(v)}}(1)/N)$
is nilpotent (being a subgroup of a nilpotent group), we obtain that
$\widetilde{\psi }(\textrm{St}_{\mathfrak{K(v)}}(1)/N)$
is nilpotent (being a subgroup of a nilpotent group), we obtain that
![]() $\textrm{St}_{\mathfrak{K(v)}}(1)/N$
is nilpotent. This implies that
$\textrm{St}_{\mathfrak{K(v)}}(1)/N$
is nilpotent. This implies that
![]() $\textrm{St}_{\mathfrak{K(v)}}(1)/{\mathfrak{K(v)}}^{\prime\prime}$
is nilpotent as it is a quotient of
$\textrm{St}_{\mathfrak{K(v)}}(1)/{\mathfrak{K(v)}}^{\prime\prime}$
is nilpotent as it is a quotient of
![]() $\textrm{St}_{\mathfrak{K(v)}}(1)/N$
. As the subgroup
$\textrm{St}_{\mathfrak{K(v)}}(1)/N$
. As the subgroup
![]() $\textrm{St}_{\mathfrak{K(v)}}(1)$
has finite index in
$\textrm{St}_{\mathfrak{K(v)}}(1)$
has finite index in
![]() $\mathfrak{K(v)}$
, the group
$\mathfrak{K(v)}$
, the group
![]() $\textrm{St}_{\mathfrak{K(v)}}(1)/\mathfrak{K(v)}^{\prime\prime}$
has finite index in
$\textrm{St}_{\mathfrak{K(v)}}(1)/\mathfrak{K(v)}^{\prime\prime}$
has finite index in
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime\prime}$
, and hence,
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime\prime}$
, and hence,
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime\prime}$
is virtually nilpotent. The last part of the result follows from [Reference Francoeur9, Corollary 5.1.3].
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime\prime}$
is virtually nilpotent. The last part of the result follows from [Reference Francoeur9, Corollary 5.1.3].
Hereafter, for
![]() $g,h \in \mathfrak{K(v)}$
, the equivalence
$g,h \in \mathfrak{K(v)}$
, the equivalence
![]() $g \equiv h \mod \mathfrak{K(v)}^{\prime}$
will simply be denoted by
$g \equiv h \mod \mathfrak{K(v)}^{\prime}$
will simply be denoted by
![]() $g \equiv h$
. Notice that for every
$g \equiv h$
. Notice that for every
![]() $z \in \mathfrak{K(v)}^{\prime}$
, we have
$z \in \mathfrak{K(v)}^{\prime}$
, we have
![]() $\sigma _z =1$
and
$\sigma _z =1$
and
![]() $\mathfrak{K(v)}^{\prime} \leq \textrm{St}_{\mathfrak{K(v)}}(1)$
. Recall also from Subsection 2.1 the map
$\mathfrak{K(v)}^{\prime} \leq \textrm{St}_{\mathfrak{K(v)}}(1)$
. Recall also from Subsection 2.1 the map
![]() $\varphi _u$
for
$\varphi _u$
for
![]() $u\in X^*$
. For convenience, we introduce the following notation. For
$u\in X^*$
. For convenience, we introduce the following notation. For
![]() $i \in [0,s-2]$
and
$i \in [0,s-2]$
and
![]() $j \in [0,m-1]$
, we define
$j \in [0,m-1]$
, we define
 \begin{align*} \delta _{j}(a_i) = \begin{cases} a_i &\text{ if } x_i = j,\\ 1 &\text{otherwise}, \end{cases} \end{align*}
\begin{align*} \delta _{j}(a_i) = \begin{cases} a_i &\text{ if } x_i = j,\\ 1 &\text{otherwise}, \end{cases} \end{align*}
and extend
![]() $\delta _j$
to a homomorphism on
$\delta _j$
to a homomorphism on
![]() $S^*$
.
$S^*$
.
Lemma 5.2.
Let
![]() ${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
${\mathfrak{v}} = x_0 \cdots x_{s-2}$
be a word in the alphabet
![]() $X$
, and let
$X$
, and let
![]() $g \in \mathfrak{K(v)}$
be such that
$g \in \mathfrak{K(v)}$
be such that
![]() $g \equiv a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}}$
, where
$g \equiv a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}}$
, where
![]() $\epsilon _{i}\in \{\pm 1\}$
. For
$\epsilon _{i}\in \{\pm 1\}$
. For
![]() $j \in \mathbb{N}_0$
, write
$j \in \mathbb{N}_0$
, write
![]() $j = \ell s +r$
, where
$j = \ell s +r$
, where
![]() $\ell \in \mathbb{N}_0$
and
$\ell \in \mathbb{N}_0$
and
![]() $r \in [0, s-1]$
. If
$r \in [0, s-1]$
. If
![]() $\psi _j(g^{m^j})=(g_0,\dots,g_{m^j-1})$
then
$\psi _j(g^{m^j})=(g_0,\dots,g_{m^j-1})$
then
![]() $g_k \equiv a_{s-1-r}^{\epsilon _{s-1}} \cdots a_{0-r}^{\epsilon _{0}}$
for all
$g_k \equiv a_{s-1-r}^{\epsilon _{s-1}} \cdots a_{0-r}^{\epsilon _{0}}$
for all
![]() $k \in{[0, m^j-1]}$
.
$k \in{[0, m^j-1]}$
.
Proof. Since
![]() $g \equiv a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}}$
, there exists an element
$g \equiv a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}}$
, there exists an element
![]() $(z_0,\dots,z_{m-1})= z \in \mathfrak{K(v)}^{\prime}$
such that
$(z_0,\dots,z_{m-1})= z \in \mathfrak{K(v)}^{\prime}$
such that
![]() $g = a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}} z$
. Suppose that
$g = a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}} z$
. Suppose that
![]() $\epsilon _0 = 1$
. We have that the section of
$\epsilon _0 = 1$
. We have that the section of
![]() $g$
at the vertex
$g$
at the vertex
![]() $j$
is
$j$
is
 \begin{align*} (a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}} z)_j= \begin{cases} \delta _j(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1} )z_{j+1} & \text{ if } j \in [0,m-2],\\ \delta _{m-1}(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1} ) a_{s-1}z_0 & \text{ if } j = m-1. \end{cases} \end{align*}
\begin{align*} (a_{s-1}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{0}} z)_j= \begin{cases} \delta _j(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1} )z_{j+1} & \text{ if } j \in [0,m-2],\\ \delta _{m-1}(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1} ) a_{s-1}z_0 & \text{ if } j = m-1. \end{cases} \end{align*}
Therefore, for
![]() $j \in [0,m-1]$
, the element
$j \in [0,m-1]$
, the element
![]() $\varphi _j(g^m)$
is equal to the product
$\varphi _j(g^m)$
is equal to the product
 \begin{align*} &\big (\delta _j(a_{s-2}^{\epsilon _{s-1}} \cdots a_0^{\epsilon _1} )z_{j+1}\big )\cdot \,\cdots \,\cdot \big ( \delta _{m-2}( a_{s-2}^{\epsilon _{s-1}} \cdots a_0^{\epsilon _1})z_{m-1} \big )\cdot \\ &\qquad \qquad \big (\delta _{m-1}(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1}) a_{s-1}z_0\big )\cdot \\ &\big (\delta _0(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1})z_{1}\big )\cdot \,\cdots \,\cdot \big ( \delta _{j-1}(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1})z_{j}\big ). \end{align*}
\begin{align*} &\big (\delta _j(a_{s-2}^{\epsilon _{s-1}} \cdots a_0^{\epsilon _1} )z_{j+1}\big )\cdot \,\cdots \,\cdot \big ( \delta _{m-2}( a_{s-2}^{\epsilon _{s-1}} \cdots a_0^{\epsilon _1})z_{m-1} \big )\cdot \\ &\qquad \qquad \big (\delta _{m-1}(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1}) a_{s-1}z_0\big )\cdot \\ &\big (\delta _0(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1})z_{1}\big )\cdot \,\cdots \,\cdot \big ( \delta _{j-1}(a_{s-2}^{\epsilon _{s-1}}\cdots a_0^{\epsilon _1})z_{j}\big ). \end{align*}
Since
![]() $\delta _k(a_i^{\epsilon _{i+1}})$
is non-trivial for only one
$\delta _k(a_i^{\epsilon _{i+1}})$
is non-trivial for only one
![]() $k \in [0,m-1]$
, we get that
$k \in [0,m-1]$
, we get that
![]() $\varphi _j(g^m) \equiv a_{s-2}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{1}}a_{s-1}^{\epsilon _{0}}$
for all
$\varphi _j(g^m) \equiv a_{s-2}^{\epsilon _{s-1}} \cdots a_{0}^{\epsilon _{1}}a_{s-1}^{\epsilon _{0}}$
for all
![]() $j \in{[0, m-1]}$
, since
$j \in{[0, m-1]}$
, since
![]() $z_0 \cdots z_{m-1} \in \mathfrak{K(v)}^{\prime}$
by Lemma 2.1. The case
$z_0 \cdots z_{m-1} \in \mathfrak{K(v)}^{\prime}$
by Lemma 2.1. The case
![]() $\epsilon _0 = -1$
follows in a similar way. The result then follows upon repeating the above process.
$\epsilon _0 = -1$
follows in a similar way. The result then follows upon repeating the above process.
In the following, we denote by
![]() $\textrm{Sym}(s)$
the symmetric group on
$\textrm{Sym}(s)$
the symmetric group on
![]() $[0,s-1]$
.
$[0,s-1]$
.
Lemma 5.3.
Let
![]() ${\mathfrak{v}}=t\,\overset{s-1}\dots \,t$
be a constant word, where
${\mathfrak{v}}=t\,\overset{s-1}\dots \,t$
be a constant word, where
![]() $t\in [0,m-1]$
. Let
$t\in [0,m-1]$
. Let
![]() $g=a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in \mathfrak{K(v)}$
where
$g=a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in \mathfrak{K(v)}$
where
![]() $\pi \in \textrm{Sym}(s)$
and
$\pi \in \textrm{Sym}(s)$
and
![]() $\epsilon _i \in \{\pm 1\}$
. For
$\epsilon _i \in \{\pm 1\}$
. For
![]() $j \in \mathbb{N}_0$
, write
$j \in \mathbb{N}_0$
, write
![]() $j = \ell s +r$
, where
$j = \ell s +r$
, where
![]() $\ell \in \mathbb{N}_0$
and
$\ell \in \mathbb{N}_0$
and
![]() $r \in [0, s-1]$
. Then
$r \in [0, s-1]$
. Then
![]() $\varphi _{t^j}(g^{m^j})=a_{(s-1)^{\pi }-r}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }-r}^{\epsilon _{0^{\pi }}}$
.
$\varphi _{t^j}(g^{m^j})=a_{(s-1)^{\pi }-r}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }-r}^{\epsilon _{0^{\pi }}}$
.
Proof. Let
![]() $i \in{[0, s-1]}$
be such that
$i \in{[0, s-1]}$
be such that
![]() $0 = i ^{\pi }$
. Then
$0 = i ^{\pi }$
. Then
 \begin{align*} g&= a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }}^{\epsilon _{(i+1)^{\pi }}}a_0^{\epsilon _{0}}a_{(i-1)^{\pi }}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}\\ &={\begin{cases}(1,\overset{t-1}\dots,1, a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}, 1,\ldots,1,a_{s-1})\sigma & \text{ if } \epsilon _0 =1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}, 1,\ldots,1,a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}})\sigma & \text{ if } \epsilon _0 =1\text{ and }t=0,\\ (a_{s-1}^{-1},1,\overset{t-1}\dots,1,a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}, a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},1,\ldots,1)\sigma ^{-1} & \text{ if } \epsilon _0 =-1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1}, a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},1,\ldots,1)\sigma ^{-1} & \text{ if } \epsilon _0 =-1\text{ and }t=0. \end{cases} } \end{align*}
\begin{align*} g&= a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }}^{\epsilon _{(i+1)^{\pi }}}a_0^{\epsilon _{0}}a_{(i-1)^{\pi }}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}\\ &={\begin{cases}(1,\overset{t-1}\dots,1, a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}, 1,\ldots,1,a_{s-1})\sigma & \text{ if } \epsilon _0 =1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}, 1,\ldots,1,a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}})\sigma & \text{ if } \epsilon _0 =1\text{ and }t=0,\\ (a_{s-1}^{-1},1,\overset{t-1}\dots,1,a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}, a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},1,\ldots,1)\sigma ^{-1} & \text{ if } \epsilon _0 =-1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1}, a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},1,\ldots,1)\sigma ^{-1} & \text{ if } \epsilon _0 =-1\text{ and }t=0. \end{cases} } \end{align*}
By taking the
![]() $m$
th power of the element
$m$
th power of the element
![]() $g$
we get
$g$
we get
 \begin{align*} g^m= {\begin{cases}(*,\overset{t}\dots,*,a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#) & \text{ if } \epsilon _0 =1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#) & \text{ if } \epsilon _0 =1\text{ and }t=0,\\ (*,\overset{t}\dots,*,a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1} a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#) & \text{ if } \epsilon _0 =-1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1} a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#)\sigma ^{-1} & \text{ if } \epsilon _0 =-1\text{ and }t=0. \end{cases}} \end{align*}
\begin{align*} g^m= {\begin{cases}(*,\overset{t}\dots,*,a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#) & \text{ if } \epsilon _0 =1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#) & \text{ if } \epsilon _0 =1\text{ and }t=0,\\ (*,\overset{t}\dots,*,a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1} a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#) & \text{ if } \epsilon _0 =-1\text{ and }t\gt 0,\\ (a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1} a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}},\#,\ldots,\#)\sigma ^{-1} & \text{ if } \epsilon _0 =-1\text{ and }t=0. \end{cases}} \end{align*}
where
 \begin{align*} * = \begin{cases}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1} & \text{ if } \epsilon _0 =1, \\ \qquad &\\ a_{s-1}^{-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} & \text{ if } \epsilon _0 = -1, \end{cases} \end{align*}
\begin{align*} * = \begin{cases}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1} & \text{ if } \epsilon _0 =1, \\ \qquad &\\ a_{s-1}^{-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} & \text{ if } \epsilon _0 = -1, \end{cases} \end{align*}
and
 \begin{align*} \# = \begin{cases}a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} & \text{ if } \epsilon _0 =1, \\ &\\ a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1} & \text{ if } \epsilon _0 = -1. \end{cases} \end{align*}
\begin{align*} \# = \begin{cases}a_{s-1}a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}} & \text{ if } \epsilon _0 =1, \\ &\\ a_{(i-1)^{\pi }-1}^{\epsilon _{(i-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{(i+1)^{\pi }-1}^{\epsilon _{(i+1)^{\pi }}}a_{s-1}^{-1} & \text{ if } \epsilon _0 = -1. \end{cases} \end{align*}
In particular, we have
![]() $\varphi _{t}(g^{m})=a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}$
, and the result follows recursively.
$\varphi _{t}(g^{m})=a_{(s-1)^{\pi }-1}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }-1}^{\epsilon _{0^{\pi }}}$
, and the result follows recursively.
We recall that
![]() $H_u$
denotes the subgroup
$H_u$
denotes the subgroup
![]() $\varphi _u(\textrm{st}_H(u))$
for a vertex
$\varphi _u(\textrm{st}_H(u))$
for a vertex
![]() $u \in X^*$
. By Lemma 3.2, the group
$u \in X^*$
. By Lemma 3.2, the group
![]() $\mathfrak{K(v)}$
is fractal, so
$\mathfrak{K(v)}$
is fractal, so
![]() $ \mathfrak{K(v)}_u= \mathfrak{K(v)}$
for all
$ \mathfrak{K(v)}_u= \mathfrak{K(v)}$
for all
![]() $u \in X^*$
.
$u \in X^*$
.
Lemma 5.4.
Let
![]() ${\mathfrak{v}}=t\,\overset{s-1}\dots \, t$
be a constant word, where
${\mathfrak{v}}=t\,\overset{s-1}\dots \, t$
be a constant word, where
![]() $t\in [0,m-1]$
, and let
$t\in [0,m-1]$
, and let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathfrak{K(v)}$
. Assume that
$\mathfrak{K(v)}$
. Assume that
![]() $a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in H$
for some
$a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in H$
for some
![]() $\pi \in \textrm{Sym}(s)$
, where
$\pi \in \textrm{Sym}(s)$
, where
![]() $\epsilon _i \in \{\pm 1\}$
. Then the following assertions hold.
$\epsilon _i \in \{\pm 1\}$
. Then the following assertions hold.
-
(i) For each
 $n \in \mathbb{N}$
and vertex
$n \in \mathbb{N}$
and vertex
 $u$
of level
$u$
of level
 $ns$
, the subgroup
$ns$
, the subgroup
 $H_u$
contains a cyclic permutation of the word
$H_u$
contains a cyclic permutation of the word
 $a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
.
$a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
. -
(ii) Furthermore, if
 $\epsilon _i=1$
for some
$\epsilon _i=1$
for some
 $i\in [0,s]$
, then for each
$i\in [0,s]$
, then for each
 $n \in \mathbb{N}$
, there is a vertex
$n \in \mathbb{N}$
, there is a vertex
 $u$
of level
$u$
of level
 $ns$
such that the cyclic permutation
$ns$
such that the cyclic permutation
 $w$
of
$w$
of
 $a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
that is contained in
$a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
that is contained in
 $H_u$
satisfies the following property:
$H_u$
satisfies the following property:
-
(a) if
 $t\gt 0$
, the cyclic permutation
$t\gt 0$
, the cyclic permutation
 $w$
ends with
$w$
ends with
 $a_i$
on the right;
$a_i$
on the right;
-
(b) if
 $t=0$
, the cyclic permutation
$t=0$
, the cyclic permutation
 $w$
starts with
$w$
starts with
 $a_i$
on the left.
$a_i$
on the left.
-
Proof. (i) Let
![]() $g = a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in H$
. Then,
$g = a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in H$
. Then,
![]() $0 = i ^{\pi }$
for some
$0 = i ^{\pi }$
for some
![]() $i \in{[0, s-1]}$
. Observe from the proof of Lemma 5.3 that
$i \in{[0, s-1]}$
. Observe from the proof of Lemma 5.3 that
and that
![]() $\varphi _j(g^m)$
is a cyclic permutation of
$\varphi _j(g^m)$
is a cyclic permutation of
![]() $\varphi _{t}(g^m)$
for every
$\varphi _{t}(g^m)$
for every
![]() $j \in{[0, m-1]}$
. By repeating the process of taking powers we get that
$j \in{[0, m-1]}$
. By repeating the process of taking powers we get that
![]() ${\psi }_s(g^{m^s})=(g_0,\dots,g_{m^s-1})$
with
${\psi }_s(g^{m^s})=(g_0,\dots,g_{m^s-1})$
with
![]() $g_{\tau }= g$
, for the component
$g_{\tau }= g$
, for the component
![]() $\tau$
corresponding to the vertex
$\tau$
corresponding to the vertex
![]() $t^s$
, and
$t^s$
, and
![]() $g_k$
is a cyclic permutation of the word
$g_k$
is a cyclic permutation of the word
![]() $a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
for
$a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
for
![]() $k\in [ 0,m^s-1]$
.
$k\in [ 0,m^s-1]$
.
(ii) We will only consider the case
![]() $t\gt 0$
, as the case
$t\gt 0$
, as the case
![]() $t=0$
is analogous. In particular, if
$t=0$
is analogous. In particular, if
![]() $\epsilon _0 =1$
, we note from the proof of Lemma 5.3 that
$\epsilon _0 =1$
, we note from the proof of Lemma 5.3 that
and by Lemma 5.3 we see that
More generally, suppose that
![]() $\epsilon _j =1$
for
$\epsilon _j =1$
for
![]() $j\in [0,s]$
and let
$j\in [0,s]$
and let
![]() $\ell \in [0,s]$
be such that
$\ell \in [0,s]$
be such that
![]() $\ell ^\pi =j$
. Writing
$\ell ^\pi =j$
. Writing
![]() $v_j= t\overset{j}\cdots t$
and
$v_j= t\overset{j}\cdots t$
and
![]() $w_j=(t-1)t\,\overset{s-j-1}\cdots \, t$
, we recall from Lemma 5.3 that
$w_j=(t-1)t\,\overset{s-j-1}\cdots \, t$
, we recall from Lemma 5.3 that
Then similar to the above, we see that
and as
![]() $u_j\,{:\!=}\,v_jw_j$
is a vertex of level
$u_j\,{:\!=}\,v_jw_j$
is a vertex of level
![]() $s$
, we have that
$s$
, we have that
![]() $H_{u_j}$
contains a cyclic permutation of
$H_{u_j}$
contains a cyclic permutation of
![]() $a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
that ends with
$a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
that ends with
![]() $a_j$
on the right.
$a_j$
on the right.
Now, by using Lemma 5.3 repeatedly, one can see that the result holds for level
![]() $ns$
of
$ns$
of
![]() $T$
, for
$T$
, for
![]() $n\gt 1$
.
$n\gt 1$
.
Proposition 5.5.
Let
![]() ${\mathfrak{v}}=t\,\overset{s-1}\dots \, t$
be a constant word, where
${\mathfrak{v}}=t\,\overset{s-1}\dots \, t$
be a constant word, where
![]() $t\in [0,m-1]$
, and let
$t\in [0,m-1]$
, and let
![]() $ g \in \mathfrak{K(v)}$
be such that
$ g \in \mathfrak{K(v)}$
be such that
![]() $g \equiv a_{s-1}^{\epsilon _{s-1}}\cdots a_{0}^{\epsilon _{0}}$
, where
$g \equiv a_{s-1}^{\epsilon _{s-1}}\cdots a_{0}^{\epsilon _{0}}$
, where
![]() $\epsilon _{i}\in \{\pm 1\}$
. Then, there exists a vertex
$\epsilon _{i}\in \{\pm 1\}$
. Then, there exists a vertex
![]() $u$
of level
$u$
of level
![]() $ns$
in
$ns$
in
![]() $T$
, for some
$T$
, for some
![]() $n \in \mathbb{N}_0$
, and an element
$n \in \mathbb{N}_0$
, and an element
![]() $g^{\prime} \in \textrm{st}_{\langle g \rangle }(u)$
such that
$g^{\prime} \in \textrm{st}_{\langle g \rangle }(u)$
such that
![]() $\varphi _u(g^{\prime})=a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
for some
$\varphi _u(g^{\prime})=a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}}$
for some
![]() $\pi \in \textrm{Sym}(s)$
.
$\pi \in \textrm{Sym}(s)$
.
Proof. The proof proceeds by induction on the length of
![]() $g$
. Recall from Lemma 3.8 that
$g$
. Recall from Lemma 3.8 that
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}=\langle a_0\mathfrak{K(v)}^{\prime},\ldots,a_{s-1}\mathfrak{K(v)}^{\prime}\rangle \cong \mathbb{Z}^s$
. Hence, if
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}=\langle a_0\mathfrak{K(v)}^{\prime},\ldots,a_{s-1}\mathfrak{K(v)}^{\prime}\rangle \cong \mathbb{Z}^s$
. Hence, if
![]() $g$
is equivalent to
$g$
is equivalent to
![]() $a_{s-1}^{\epsilon _{s-1}}\cdots a_{0}^{\epsilon _{0}}$
then
$a_{s-1}^{\epsilon _{s-1}}\cdots a_{0}^{\epsilon _{0}}$
then
![]() $|g| \gt s-1$
, since any word containing each of the distinct generators of
$|g| \gt s-1$
, since any word containing each of the distinct generators of
![]() $\mathfrak{K(v)}$
has length at least
$\mathfrak{K(v)}$
has length at least
![]() $s$
. Assume that
$s$
. Assume that
![]() $\vert g \vert = s$
. Then
$\vert g \vert = s$
. Then
and the result follows trivially by choosing
![]() $u$
as the root vertex. Now, assume that
$u$
as the root vertex. Now, assume that
![]() $\vert g \vert \gt s$
. Since the exponent sum of
$\vert g \vert \gt s$
. Since the exponent sum of
![]() $a_0$
in any word representing
$a_0$
in any word representing
![]() $g$
is
$g$
is
![]() $\epsilon _0$
, we can write
$\epsilon _0$
, we can write
![]() $g = (g_0,\dots, g_{m-1})\sigma ^{\epsilon _0}$
with
$g = (g_0,\dots, g_{m-1})\sigma ^{\epsilon _0}$
with
![]() $g_0, \dots,g_{m-1}\in \mathfrak{K(v)}$
. We get
$g_0, \dots,g_{m-1}\in \mathfrak{K(v)}$
. We get
 \begin{equation*} g^m = \begin {cases}(g_0g_1\cdots g_{m-1},\,g_1\cdots g_{m-1}g_0\,,\,\dots \,,\, g_{m-1}g_0g_1\cdots g_{m-2}) & \text { if } \epsilon _0 =1,\\ (g_0g_{m-1}g_{m-2}\cdots g_1,\,g_1g_0g_{m-1}\cdots g_2\,,\,\dots \,,\, g_{m-1}g_{m-2}\cdots g_{0}) & \text { if } \epsilon _0 = -1. \end {cases} \end{equation*}
\begin{equation*} g^m = \begin {cases}(g_0g_1\cdots g_{m-1},\,g_1\cdots g_{m-1}g_0\,,\,\dots \,,\, g_{m-1}g_0g_1\cdots g_{m-2}) & \text { if } \epsilon _0 =1,\\ (g_0g_{m-1}g_{m-2}\cdots g_1,\,g_1g_0g_{m-1}\cdots g_2\,,\,\dots \,,\, g_{m-1}g_{m-2}\cdots g_{0}) & \text { if } \epsilon _0 = -1. \end {cases} \end{equation*}
For every
![]() $k \in{[0, m-1]}$
, we set
$k \in{[0, m-1]}$
, we set
![]() $\alpha _k = \varphi _{k}(g^m)$
. It follows from Lemma 5.2 that
$\alpha _k = \varphi _{k}(g^m)$
. It follows from Lemma 5.2 that
for all
![]() $k \in{[0, m-1]}$
. Furthermore,
$k \in{[0, m-1]}$
. Furthermore,
![]() $\vert \alpha _k \vert \leq \vert g \vert$
for all
$\vert \alpha _k \vert \leq \vert g \vert$
for all
![]() $k \in{[0, m-1]}$
by Lemma 4.2. If there exists
$k \in{[0, m-1]}$
by Lemma 4.2. If there exists
![]() $k \in{[0, m-1]}$
such that
$k \in{[0, m-1]}$
such that
![]() $\vert \alpha _k \vert \lt \vert g \vert$
, then it follows by induction that there exists a vertex
$\vert \alpha _k \vert \lt \vert g \vert$
, then it follows by induction that there exists a vertex
![]() $u$
of level
$u$
of level
![]() $ns$
in
$ns$
in
![]() $T$
, for some
$T$
, for some
![]() $n \in \mathbb{N}_0$
, and
$n \in \mathbb{N}_0$
, and
![]() $g^{\prime} \in \textrm{st}_{\langle \alpha _k \rangle }(u)$
such that
$g^{\prime} \in \textrm{st}_{\langle \alpha _k \rangle }(u)$
such that
for some
![]() $\pi \in \textrm{Sym}(s)$
. Using Lemma 5.3, we get that
$\pi \in \textrm{Sym}(s)$
. Using Lemma 5.3, we get that
and hence, the result follows.
Assume that
![]() $\vert \alpha _k \vert = \vert g \vert$
for all
$\vert \alpha _k \vert = \vert g \vert$
for all
![]() $k \in{[0, m-1]}.$
Since
$k \in{[0, m-1]}.$
Since
![]() $\vert \alpha _k \vert \leq \sum \limits _{\ell =0}^{m-1} \vert g_{\ell } \vert$
, in particular, we get
$\vert \alpha _k \vert \leq \sum \limits _{\ell =0}^{m-1} \vert g_{\ell } \vert$
, in particular, we get
Let
![]() $w_g \in S^*$
be a geodesic word representing
$w_g \in S^*$
be a geodesic word representing
![]() $g$
. Since for each
$g$
. Since for each
![]() $i\in [0,s-1]$
the element
$i\in [0,s-1]$
the element
![]() $a_i^{\epsilon _i}$
contributes
$a_i^{\epsilon _i}$
contributes
![]() $a_{i-1}^{\epsilon _i}$
in exactly one component, we can obtain words
$a_{i-1}^{\epsilon _i}$
in exactly one component, we can obtain words
![]() $w_{g_k}$
representing
$w_{g_k}$
representing
![]() $g_k$
by substituting
$g_k$
by substituting
![]() $a_i^{\epsilon _i}$
in
$a_i^{\epsilon _i}$
in
![]() $w_g$
with
$w_g$
with
![]() $a_{i-1}^{\epsilon _i}$
in the appropriate component. Notice that
$a_{i-1}^{\epsilon _i}$
in the appropriate component. Notice that
![]() $\vert g_k\vert \leq \vert w_{g_k} \vert$
for every
$\vert g_k\vert \leq \vert w_{g_k} \vert$
for every
![]() $k \in{[0, m-1]}$
. Moreover, the words
$k \in{[0, m-1]}$
. Moreover, the words
![]() $w_{g_k}$
are geodesic. Indeed,
$w_{g_k}$
are geodesic. Indeed,
which forces that
![]() $\vert w_{g_k} \vert = \vert g_k \vert .$
Now, set
$\vert w_{g_k} \vert = \vert g_k \vert .$
Now, set
 \begin{equation*} w_{\alpha _k} = \begin {cases} w_{g_k}w_{g_{k+1}}\cdots w_{g_{k+m-1}} & \text { if } \epsilon _0 = 1,\\ w_{g_k}w_{g_{k-1}}\cdots w_{g_{k-(m-1)}} & \text { if } \epsilon _0 = -1. \end {cases} \end{equation*}
\begin{equation*} w_{\alpha _k} = \begin {cases} w_{g_k}w_{g_{k+1}}\cdots w_{g_{k+m-1}} & \text { if } \epsilon _0 = 1,\\ w_{g_k}w_{g_{k-1}}\cdots w_{g_{k-(m-1)}} & \text { if } \epsilon _0 = -1. \end {cases} \end{equation*}
Clearly,
![]() $w_{\alpha _k}$
represents
$w_{\alpha _k}$
represents
![]() $\alpha _k$
. Therefore,
$\alpha _k$
. Therefore,
![]() $\vert \alpha _k \vert \leq \vert w_{\alpha _k} \vert$
. Furthermore,
$\vert \alpha _k \vert \leq \vert w_{\alpha _k} \vert$
. Furthermore,
Thus,
![]() $\vert \alpha _k \vert = \vert w_{\alpha _k} \vert$
and
$\vert \alpha _k \vert = \vert w_{\alpha _k} \vert$
and
![]() $w_{\alpha _k}$
is a geodesic word.
$w_{\alpha _k}$
is a geodesic word.
Now, we claim that in order to prove the result, it suffices to consider the situation in which for every
![]() $i \in{[0, s-1]}$
there exists a unique
$i \in{[0, s-1]}$
there exists a unique
![]() $k \in{[0, m-1]}$
such that
$k \in{[0, m-1]}$
such that
![]() $w_{g_k}$
contains a non-trivial power of
$w_{g_k}$
contains a non-trivial power of
![]() $a_i$
. First, we consider the case when
$a_i$
. First, we consider the case when
![]() $i=0$
. Assume to the contrary that there exist distinct
$i=0$
. Assume to the contrary that there exist distinct
![]() $k_1,k_2 \in{[0, m-1]}$
such that
$k_1,k_2 \in{[0, m-1]}$
such that
![]() $w_{g_{k_1}}$
and
$w_{g_{k_1}}$
and
![]() $w_{g_{k_2}}$
contain non-trivial powers of
$w_{g_{k_2}}$
contain non-trivial powers of
![]() $a_0$
. We can reduce to the following two cases.
$a_0$
. We can reduce to the following two cases.
Case 1: Suppose that there exist distinct
![]() $k_1,k_2 \in{[0, m-1]}$
such that
$k_1,k_2 \in{[0, m-1]}$
such that
![]() $w_{g_{k_1}}$
and
$w_{g_{k_1}}$
and
![]() $w_{g_{k_2}}$
contain
$w_{g_{k_2}}$
contain
![]() $a_0$
and
$a_0$
and
![]() $a_0^{-1}$
, respectively. Then for some
$a_0^{-1}$
, respectively. Then for some
![]() $k\in{[0, m-1]}$
, the word
$k\in{[0, m-1]}$
, the word
![]() $w_{\alpha _k}$
contains a subword of the form
$w_{\alpha _k}$
contains a subword of the form
![]() $a_0 w a_0^{-1}$
with
$a_0 w a_0^{-1}$
with
![]() $w \in S^*$
. If
$w \in S^*$
. If
![]() $\alpha _k^m = (\beta _0,\dots,\beta _{m-1})$
then, by Lemma 4.2, Lemma 4.3 and Lemma 4.4, we obtain that
$\alpha _k^m = (\beta _0,\dots,\beta _{m-1})$
then, by Lemma 4.2, Lemma 4.3 and Lemma 4.4, we obtain that
![]() $\vert \beta _\ell \vert \lt \vert \alpha \vert$
for
$\vert \beta _\ell \vert \lt \vert \alpha \vert$
for
![]() $\ell \in{[0, m-1]}$
. Again, the result follows by induction.
$\ell \in{[0, m-1]}$
. Again, the result follows by induction.
Case 2: Suppose there exist distinct
![]() $k_1,k_2 \in{[0, m-1]}$
such that
$k_1,k_2 \in{[0, m-1]}$
such that
![]() $w_{g_{k_1}}$
and
$w_{g_{k_1}}$
and
![]() $w_{g_{k_2}}$
contain
$w_{g_{k_2}}$
contain
![]() $a_0$
. Recall that
$a_0$
. Recall that
![]() $\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}=\langle a_0\mathfrak{K(v)}^{\prime},\ldots,a_{s-1}\mathfrak{K(v)}^{\prime}\rangle \cong \mathbb{Z}^s$
. Hence, as the exponent sum of
$\mathfrak{K(v)}/\mathfrak{K(v)}^{\prime}=\langle a_0\mathfrak{K(v)}^{\prime},\ldots,a_{s-1}\mathfrak{K(v)}^{\prime}\rangle \cong \mathbb{Z}^s$
. Hence, as the exponent sum of
![]() $a_{1}$
in any word representing
$a_{1}$
in any word representing
![]() $g$
is
$g$
is
![]() $\epsilon _1$
, the exponent sum of
$\epsilon _1$
, the exponent sum of
![]() $a_0$
in
$a_0$
in
![]() $w_{\alpha _k}$
is equal to
$w_{\alpha _k}$
is equal to
![]() $\epsilon _1$
for all
$\epsilon _1$
for all
![]() $k \in{[0, m-1]}$
. This implies that there exists
$k \in{[0, m-1]}$
. This implies that there exists
![]() $k_3 \in{[0, m-1]}$
such that
$k_3 \in{[0, m-1]}$
such that
![]() $w_{g_{k_3}}$
contains
$w_{g_{k_3}}$
contains
![]() $a_{0}^{-1}$
, and we are in the previous case. Analogously, the same argument works if both
$a_{0}^{-1}$
, and we are in the previous case. Analogously, the same argument works if both
![]() $w_{g_{k_1}}$
and
$w_{g_{k_1}}$
and
![]() $w_{g_{k_2}}$
contain
$w_{g_{k_2}}$
contain
![]() $a_0^{-1}$
.
$a_0^{-1}$
.
We reduce to the case where there exists a unique
![]() $k \in{[0, m-1]}$
such that
$k \in{[0, m-1]}$
such that
![]() $w_{g_k}$
contains a non-trivial power of
$w_{g_k}$
contains a non-trivial power of
![]() $a_0$
. By inducting on
$a_0$
. By inducting on
![]() $i \in{[0, s-1]}$
, assume that there exists a unique
$i \in{[0, s-1]}$
, assume that there exists a unique
![]() $k \in{[0, m-1]}$
such that
$k \in{[0, m-1]}$
such that
![]() $w_{g_k}$
contains a non-trivial power of
$w_{g_k}$
contains a non-trivial power of
![]() $a_{i-1}$
. Then suppose that there exist distinct
$a_{i-1}$
. Then suppose that there exist distinct
![]() $k_1,k_2 \in{[0, m-1]}$
such that
$k_1,k_2 \in{[0, m-1]}$
such that
![]() $w_{g_{k_1}}$
and
$w_{g_{k_1}}$
and
![]() $w_{g_{k_2}}$
contain non-trivial powers of
$w_{g_{k_2}}$
contain non-trivial powers of
![]() $a_{i}$
. We can find
$a_{i}$
. We can find
![]() $k_3 \in{[0, m-1]}$
such that
$k_3 \in{[0, m-1]}$
such that
![]() $w_{\alpha _{k_3}}$
contains a subword of the form
$w_{\alpha _{k_3}}$
contains a subword of the form
![]() $a_{i} ^{\ell _1}wa_{i} ^{\ell _2}$
, where
$a_{i} ^{\ell _1}wa_{i} ^{\ell _2}$
, where
![]() $\ell _1,\ell _2 \in \mathbb{Z}\backslash \{0\}$
and
$\ell _1,\ell _2 \in \mathbb{Z}\backslash \{0\}$
and
![]() $w \in S^*$
with exponent sum of
$w \in S^*$
with exponent sum of
![]() $a_0$
in
$a_0$
in
![]() $w$
is not equal to
$w$
is not equal to
![]() $0 \bmod m$
. Thanks to Lemma 5.2, we may replace
$0 \bmod m$
. Thanks to Lemma 5.2, we may replace
![]() $g$
with
$g$
with
![]() $\alpha _{k_3}$
. Then we find more than one
$\alpha _{k_3}$
. Then we find more than one
![]() $w_{g_k}$
containing non-trivial powers of
$w_{g_k}$
containing non-trivial powers of
![]() $a_{i-1}$
, contradicting the induction hypothesis and hence proving the claim.
$a_{i-1}$
, contradicting the induction hypothesis and hence proving the claim.
Thus, we reduce to the situation in which for every
![]() $i \in{[0, s-1]}$
there exists a unique
$i \in{[0, s-1]}$
there exists a unique
![]() $k \in{[0, m-1]}$
such that
$k \in{[0, m-1]}$
such that
![]() $w_{g_k}$
contains a non-trivial power of
$w_{g_k}$
contains a non-trivial power of
![]() $a_i$
. An easy computation yields that
$a_i$
. An easy computation yields that
![]() $w_{g}$
does not contain a subword of the form
$w_{g}$
does not contain a subword of the form
![]() $a_{i}^{\ell _1}wa_{i}^{\ell _2}$
, for some
$a_{i}^{\ell _1}wa_{i}^{\ell _2}$
, for some
![]() $i \in{[0, s-1]}$
where
$i \in{[0, s-1]}$
where
![]() $\ell _1,\ell _2 \in \mathbb{Z}\backslash \{0\}$
and
$\ell _1,\ell _2 \in \mathbb{Z}\backslash \{0\}$
and
![]() $w \in S^*$
with the exponent sum of
$w \in S^*$
with the exponent sum of
![]() $a_0$
in
$a_0$
in
![]() $w$
being not equal to
$w$
being not equal to
![]() $0 \bmod m$
. Hence, we conclude that
$0 \bmod m$
. Hence, we conclude that
![]() $w_g$
must be of the form
$w_g$
must be of the form
where
![]() $w_1$
and
$w_1$
and
![]() $w_2$
are words in the given elements, and
$w_2$
are words in the given elements, and
![]() $\{i_1,\dots,i_r,i_{r+1},\dots,i_{s-1}\}={[1, s-1]}$
such that the intersection
$\{i_1,\dots,i_r,i_{r+1},\dots,i_{s-1}\}={[1, s-1]}$
such that the intersection
![]() $\{i_1,\dots,{i_r} \} \cap \{i_{r+1},\dots,i_{s-1}\}$
is empty. Consider the element
$\{i_1,\dots,{i_r} \} \cap \{i_{r+1},\dots,i_{s-1}\}$
is empty. Consider the element
![]() $\alpha _{t}$
obtained from the element
$\alpha _{t}$
obtained from the element
![]() $g$
above. Then, the corresponding
$g$
above. Then, the corresponding
![]() $w_{\alpha _t}$
has the form
$w_{\alpha _t}$
has the form
and continuing the above procedure with this word yields the element
![]() $a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in H_u$
for some
$a_{(s-1)^{\pi }}^{\epsilon _{(s-1)^{\pi }}}\cdots a_{0^{\pi }}^{\epsilon _{0^{\pi }}} \in H_u$
for some
![]() $u$
of level
$u$
of level
![]() $ns$
in
$ns$
in
![]() $T$
, for some
$T$
, for some
![]() $n \in \mathbb{N}_0$
.
$n \in \mathbb{N}_0$
.
Theorem 5.6.
Let
![]() ${\mathfrak{v}}=t\,\overset{s-1}\dots \,t$
be a constant word, where
${\mathfrak{v}}=t\,\overset{s-1}\dots \,t$
be a constant word, where
![]() $t\in [0,m-1]$
. If
$t\in [0,m-1]$
. If
![]() $H$
is a prodense subgroup of
$H$
is a prodense subgroup of
![]() $\mathfrak{K(v)}$
, then
$\mathfrak{K(v)}$
, then
![]() $H = \mathfrak{K(v)}$
.
$H = \mathfrak{K(v)}$
.
Proof. Note that
![]() $H\mathfrak{K(v)}^{\prime} =\mathfrak{K(v)}$
as
$H\mathfrak{K(v)}^{\prime} =\mathfrak{K(v)}$
as
![]() $H$
is a prodense subgroup. Therefore, there exists an element
$H$
is a prodense subgroup. Therefore, there exists an element
![]() $z \in \mathfrak{K(v)}^{\prime}$
such that
$z \in \mathfrak{K(v)}^{\prime}$
such that
![]() $ a_{s-1}\cdots a_0z\in H$
. By an application of Proposition 5.5, we can find
$ a_{s-1}\cdots a_0z\in H$
. By an application of Proposition 5.5, we can find
![]() $u\in T$
such that
$u\in T$
such that
![]() $H_{u}$
contains
$H_{u}$
contains
![]() $a_{(s-1)^{\pi }}\cdots a_{0^{\pi }}$
for some
$a_{(s-1)^{\pi }}\cdots a_{0^{\pi }}$
for some
![]() $\pi \in \textrm{Sym}(s)$
. We set
$\pi \in \textrm{Sym}(s)$
. We set
![]() $g=a_{(s-1)^{\pi }}\cdots a_{0^{\pi }}$
. Thanks to [Reference Francoeur10, Lemma 3.1], the subgroup
$g=a_{(s-1)^{\pi }}\cdots a_{0^{\pi }}$
. Thanks to [Reference Francoeur10, Lemma 3.1], the subgroup
![]() $H_u$
is again a prodense subgroup of
$H_u$
is again a prodense subgroup of
![]() $\mathfrak{K(v)}$
. Without loss of generality, we replace
$\mathfrak{K(v)}$
. Without loss of generality, we replace
![]() $H$
with
$H$
with
![]() $H_u$
.
$H_u$
.
Again, as
![]() $H$
is prodense, for some
$H$
is prodense, for some
![]() $\widetilde{z}\in \mathfrak{K(v)}^{\prime}$
we similarly have
$\widetilde{z}\in \mathfrak{K(v)}^{\prime}$
we similarly have
![]() $a_{s-1}\cdots a_1a_0^{-1}\widetilde{z}\in H$
. By Proposition 5.5, there exists a vertex
$a_{s-1}\cdots a_1a_0^{-1}\widetilde{z}\in H$
. By Proposition 5.5, there exists a vertex
![]() $u$
at level
$u$
at level
![]() $ns$
, for some
$ns$
, for some
![]() $n \in \mathbb{N}$
, such that
$n \in \mathbb{N}$
, such that
![]() $H_u$
contains an element
$H_u$
contains an element
![]() $h_0$
of the form
$h_0$
of the form
where
![]() $\tau _0 \in \textrm{Sym}(s)$
, with
$\tau _0 \in \textrm{Sym}(s)$
, with
![]() $\epsilon _{i^{\tau _0}}=-1$
if
$\epsilon _{i^{\tau _0}}=-1$
if
![]() $i^{\tau _0}=0$
and
$i^{\tau _0}=0$
and
![]() $\epsilon _{i^{\tau _0}}=1$
otherwise. Now, by Lemma 5.4(i), the subgroup
$\epsilon _{i^{\tau _0}}=1$
otherwise. Now, by Lemma 5.4(i), the subgroup
![]() $H_u$
also contains some cyclic permutation of the element
$H_u$
also contains some cyclic permutation of the element
![]() $g$
. By abuse of notation, we replace
$g$
. By abuse of notation, we replace
![]() $g$
with this cyclic permutation of
$g$
with this cyclic permutation of
![]() $g$
. We again replace
$g$
. We again replace
![]() $H$
with
$H$
with
![]() $H_u$
. Now
$H_u$
. Now
![]() $H$
contains the elements
$H$
contains the elements
![]() $g$
and
$g$
and
![]() $h_0$
. Repeating this argument
$h_0$
. Repeating this argument
![]() $s-1$
times, we may assume that
$s-1$
times, we may assume that
![]() $H$
contains the elements
$H$
contains the elements
![]() $g,h_0,\dots,h_{s-1}$
, where
$g,h_0,\dots,h_{s-1}$
, where
where
![]() $\tau _j \in \textrm{Sym}(s)$
with
$\tau _j \in \textrm{Sym}(s)$
with
![]() $\epsilon _{i^{\tau _j}}=-1$
if
$\epsilon _{i^{\tau _j}}=-1$
if
![]() $i^{\tau _j}=j$
and
$i^{\tau _j}=j$
and
![]() $\epsilon _{i^{\tau _j}}=1$
otherwise.
$\epsilon _{i^{\tau _j}}=1$
otherwise.
For the remainder of the proof, we will assume that
![]() $t\gt 0$
; the case
$t\gt 0$
; the case
![]() $t=0$
is analogous, as accounted for in Remark 5.7. Appealing to Lemma 5.4(ii), we now choose a vertex
$t=0$
is analogous, as accounted for in Remark 5.7. Appealing to Lemma 5.4(ii), we now choose a vertex
![]() $v$
, with
$v$
, with
![]() $v$
of level
$v$
of level
![]() $\widetilde{n}s$
for some
$\widetilde{n}s$
for some
![]() $\widetilde{n} \in \mathbb{N}$
, such that the cyclic permutation of
$\widetilde{n} \in \mathbb{N}$
, such that the cyclic permutation of
![]() $g$
that is contained in
$g$
that is contained in
![]() $H_v$
ends with
$H_v$
ends with
![]() $a_0$
on the right. We rename this element
$a_0$
on the right. We rename this element
![]() $g$
. So we have
$g$
. So we have
![]() $g\in H_v$
and by Lemma 5.4(i) we have a cyclic permutation of each of the elements
$g\in H_v$
and by Lemma 5.4(i) we have a cyclic permutation of each of the elements
![]() $h_0,\ldots,h_{s-1}$
in
$h_0,\ldots,h_{s-1}$
in
![]() $H_v$
. By abuse of notation, we rename these cyclic permutations
$H_v$
. By abuse of notation, we rename these cyclic permutations
![]() $h_0,\ldots,h_{s-1}$
respectively. As before we replace
$h_0,\ldots,h_{s-1}$
respectively. As before we replace
![]() $H$
with
$H$
with
![]() $H_v$
. Now
$H_v$
. Now
![]() $H$
contains the elements
$H$
contains the elements
![]() $g,h_0,\dots,h_{s-1}$
, where
$g,h_0,\dots,h_{s-1}$
, where
![]() $g$
ends with
$g$
ends with
![]() $a_0$
on the right.
$a_0$
on the right.
For each
![]() $n \in \mathbb{N}_0$
, let
$n \in \mathbb{N}_0$
, let
![]() $v_n=t \,\overset{n}\dots \, t$
. It follows from Lemma 5.3 that for
$v_n=t \,\overset{n}\dots \, t$
. It follows from Lemma 5.3 that for
![]() $d\in \mathbb{N}$
,
$d\in \mathbb{N}$
,
![]() $\varphi _{v_{ds}}(g^{m^{ds}})=g$
and
$\varphi _{v_{ds}}(g^{m^{ds}})=g$
and
![]() $\varphi _{v_{ds}}(h_i^{\,m^{ds}})=h_i$
where
$\varphi _{v_{ds}}(h_i^{\,m^{ds}})=h_i$
where
![]() $i\in [0,s-1]$
. Furthermore, for any element
$i\in [0,s-1]$
. Furthermore, for any element
![]() $f \in \mathfrak{K(v)}$
of the form
$f \in \mathfrak{K(v)}$
of the form
for pairwise distinct
![]() $\iota _1,\ldots,\iota _{b}\in [0,s-1]$
with
$\iota _1,\ldots,\iota _{b}\in [0,s-1]$
with
![]() ${b}\in [1,s]$
and
${b}\in [1,s]$
and
![]() $\epsilon _i\in \{\pm 1\}$
, we can consider its contribution to
$\epsilon _i\in \{\pm 1\}$
, we can consider its contribution to
![]() $H_{v_n}$
. Specifically, if
$H_{v_n}$
. Specifically, if
![]() $f \in \textrm{St}_{\mathfrak{K(v)}}(1)$
, we simply consider its image under
$f \in \textrm{St}_{\mathfrak{K(v)}}(1)$
, we simply consider its image under
![]() $\varphi _{t}$
. If
$\varphi _{t}$
. If
![]() $f \notin \textrm{St}_{\mathfrak{K(v)}}(1)$
, then we consider
$f \notin \textrm{St}_{\mathfrak{K(v)}}(1)$
, then we consider
![]() $\varphi _{t}(f^m)$
. We refer to this general process as projecting along the path
$\varphi _{t}(f^m)$
. We refer to this general process as projecting along the path
![]() $t_{\infty }\,{:\!=}\,tt\cdots$
. By projecting along this path, we observe that if
$t_{\infty }\,{:\!=}\,tt\cdots$
. By projecting along this path, we observe that if
![]() $f \in H_{v_j}$
, for
$f \in H_{v_j}$
, for
![]() $j \in \mathbb{N}$
, then
$j \in \mathbb{N}$
, then
![]() $f \in H_{v_{j+s}}$
; compare the proof of Lemma 5.3. This observation will be used repeatedly throughout the proof without special mention.
$f \in H_{v_{j+s}}$
; compare the proof of Lemma 5.3. This observation will be used repeatedly throughout the proof without special mention.
The strategy of the proof is now to consider the contributions from
to
![]() $H_{v_n}$
and to multiply them appropriately to separate the generators
$H_{v_n}$
and to multiply them appropriately to separate the generators
![]() $a_0,\ldots,a_{s-1}$
. More specifically, if for some
$a_0,\ldots,a_{s-1}$
. More specifically, if for some
![]() $n\in \mathbb{N}$
, suppose we have non-trivial distinct elements
$n\in \mathbb{N}$
, suppose we have non-trivial distinct elements
![]() $\alpha,\beta \in H_{v_n}$
of the form
$\alpha,\beta \in H_{v_n}$
of the form
where
![]() $\epsilon _i,\delta _j\in \{\pm 1\}$
and
$\epsilon _i,\delta _j\in \{\pm 1\}$
and
![]() $2\le{q},r\le s$
, with
$2\le{q},r\le s$
, with
![]() $i_1,\ldots,i_{q}\in [0,s-1]$
pairwise distinct, and also
$i_1,\ldots,i_{q}\in [0,s-1]$
pairwise distinct, and also
![]() $j_1,\ldots,j_r\in [0,s-1]$
pairwise distinct. We consider two situations below, where we assume always that
$j_1,\ldots,j_r\in [0,s-1]$
pairwise distinct. We consider two situations below, where we assume always that
![]() $\widetilde{\alpha },\widetilde{\beta }$
are non-trivial.
$\widetilde{\alpha },\widetilde{\beta }$
are non-trivial.
-
(i) If
 $\alpha = \widetilde{\alpha }a_0$
and
$\alpha = \widetilde{\alpha }a_0$
and
 $\beta = \widetilde{\beta }a_0^{-1}\widehat{\beta }$
, thenyields
$\beta = \widetilde{\beta }a_0^{-1}\widehat{\beta }$
, thenyields \begin{equation*} \beta \alpha =\widetilde {\beta }a_0^{-1}\widehat {\beta }\widetilde {\alpha }a_0 \end{equation*}
and hence
\begin{equation*} \beta \alpha =\widetilde {\beta }a_0^{-1}\widehat {\beta }\widetilde {\alpha }a_0 \end{equation*}
and hence \begin{equation*} \varphi _{t}(\widetilde {\beta })\in H_{v_{n+1}}, \end{equation*}
\begin{equation*} \varphi _{t}(\widetilde {\beta })\in H_{v_{n+1}}, \end{equation*}
 \begin{equation*} \widetilde {\beta }\in H_{v_{n+s}}\qquad \text {and}\qquad a_0^{-1}\widehat {\beta }\in H_{v_{n+s}}. \end{equation*}
\begin{equation*} \widetilde {\beta }\in H_{v_{n+s}}\qquad \text {and}\qquad a_0^{-1}\widehat {\beta }\in H_{v_{n+s}}. \end{equation*}
-
(ii) If
 $ \alpha = a_0\widetilde{\alpha }$
and
$ \alpha = a_0\widetilde{\alpha }$
and
 $\beta = \widehat{\beta }a_0^{-1}\widetilde{\beta }$
, fromwe obtain
$\beta = \widehat{\beta }a_0^{-1}\widetilde{\beta }$
, fromwe obtain \begin{equation*} \alpha \beta =a_0\widetilde {\alpha }\widehat {\beta }a_0^{-1}\widetilde {\beta }, \end{equation*}
and similarly,
\begin{equation*} \alpha \beta =a_0\widetilde {\alpha }\widehat {\beta }a_0^{-1}\widetilde {\beta }, \end{equation*}
and similarly, \begin{equation*} \varphi _{t}(\widetilde {\beta })\in H_{v_{n+1}}, \end{equation*}
\begin{equation*} \varphi _{t}(\widetilde {\beta })\in H_{v_{n+1}}, \end{equation*}
 \begin{equation*} \widetilde {\beta }\in H_{v_{n+s}}\qquad \text {and}\qquad \widehat {\beta }a_0^{-1}\in H_{v_{n+s}}. \end{equation*}
\begin{equation*} \widetilde {\beta }\in H_{v_{n+s}}\qquad \text {and}\qquad \widehat {\beta }a_0^{-1}\in H_{v_{n+s}}. \end{equation*}
In other words, upon replacing
![]() $H_{v_n}$
with
$H_{v_n}$
with
![]() $H_{v_{n+s}}$
we have split
$H_{v_{n+s}}$
we have split
![]() $\beta \in H_{v_{n+s}}$
into two non-trivial parts. The plan is to repeatedly perform such operations as in (i) and (ii) above to keep splitting the products of generators. Eventually we will end up with
$\beta \in H_{v_{n+s}}$
into two non-trivial parts. The plan is to repeatedly perform such operations as in (i) and (ii) above to keep splitting the products of generators. Eventually we will end up with
![]() $a_0,\ldots,a_{s-1}\in H_u$
for some
$a_0,\ldots,a_{s-1}\in H_u$
for some
![]() $u$
, which gives
$u$
, which gives
![]() $H_u=\mathfrak{K(v)}$
and equivalently that
$H_u=\mathfrak{K(v)}$
and equivalently that
![]() $H=\mathfrak{K(v)}$
, as required.
$H=\mathfrak{K(v)}$
, as required.
We begin by first considering the contributions from
![]() $\langle g\rangle$
and
$\langle g\rangle$
and
![]() $\langle h_0\rangle$
along the path
$\langle h_0\rangle$
along the path
![]() $t_{\infty }$
of the tree. For convenience, write
$t_{\infty }$
of the tree. For convenience, write
for some
![]() $d\in [1,s]$
, where
$d\in [1,s]$
, where
![]() $\{i_1,\ldots,i_{s-1}\}=\{j_1,\ldots,j_{d-1},j_{d+1},\ldots,j_s\}=[1,s-1]$
.
$\{i_1,\ldots,i_{s-1}\}=\{j_1,\ldots,j_{d-1},j_{d+1},\ldots,j_s\}=[1,s-1]$
.
Case 1: Suppose
![]() $1\lt d\lt s$
. Then we are in situation (i) from above, and it follows that
$1\lt d\lt s$
. Then we are in situation (i) from above, and it follows that
We will now use (the projections of) these two parts of
![]() $h_0$
to split
$h_0$
to split
![]() $g$
into two non-trivial parts.
$g$
into two non-trivial parts.
Let
![]() $j\,{:\!=}\,j_{d-1}$
. We consider the contribution of
$j\,{:\!=}\,j_{d-1}$
. We consider the contribution of
![]() $a_{j_1}\cdots a_{j_{d-1}}$
to
$a_{j_1}\cdots a_{j_{d-1}}$
to
![]() $H_{v_j}$
. In other words, we project along the path
$H_{v_j}$
. In other words, we project along the path
![]() $t_{\infty }$
down to level
$t_{\infty }$
down to level
![]() $j$
, which gives
$j$
, which gives
Recalling that
![]() $g=a_{i_1}\cdots a_{i_{s-1}}a_0$
, we have that
$g=a_{i_1}\cdots a_{i_{s-1}}a_0$
, we have that
![]() $i_r=j$
for some
$i_r=j$
for some
![]() $r\in [1,s-1]$
. Then setting
$r\in [1,s-1]$
. Then setting
and
it follows from situation (i) that
so we have split
![]() $g$
into two non-trivial parts.
$g$
into two non-trivial parts.
We now use the two parts of
![]() $g$
to split the parts of
$g$
to split the parts of
![]() $h_0$
further. For clarity, let us first project to
$h_0$
further. For clarity, let us first project to
![]() $v_s$
. Here in
$v_s$
. Here in
![]() $H_{v_s}$
we have the elements
$H_{v_s}$
we have the elements
The left two elements are the two parts of
![]() $h_0$
, and the right two are those of
$h_0$
, and the right two are those of
![]() $g$
. Without loss of generality, we replace
$g$
. Without loss of generality, we replace
![]() $H$
with
$H$
with
![]() $H_{v_s}$
.
$H_{v_s}$
.
Subcase (a): Suppose
![]() $1\lt r\lt s-1$
. Let
$1\lt r\lt s-1$
. Let
![]() $k\,{:\!=}\,i_1$
. Then either
$k\,{:\!=}\,i_1$
. Then either
![]() $k=j_{q}$
for
$k=j_{q}$
for
![]() ${q}\in [1,d-2]$
or
${q}\in [1,d-2]$
or
![]() $k=j_{q}$
for
$k=j_{q}$
for
![]() ${q}\in [d+1,s]$
. Suppose the former; a similar argument works for the latter. If
${q}\in [d+1,s]$
. Suppose the former; a similar argument works for the latter. If
![]() ${q}\gt 1$
, we let
${q}\gt 1$
, we let
![]() $\beta ^{-1}$
be the
$\beta ^{-1}$
be the
![]() $k$
th level projection of
$k$
th level projection of
![]() $a_{j_1}\cdots a_{j_{d-2}}a_j$
(as usual along the path
$a_{j_1}\cdots a_{j_{d-2}}a_j$
(as usual along the path
![]() $t_{\infty }$
) and
$t_{\infty }$
) and
![]() $\alpha$
be that of
$\alpha$
be that of
![]() $a_ka_{i_2}\cdots a_{i_{r-1}}a_j$
, which by (ii) gives, upon replacing
$a_ka_{i_2}\cdots a_{i_{r-1}}a_j$
, which by (ii) gives, upon replacing
![]() $H$
with
$H$
with
![]() $H_{v_s}$
, the following elements in
$H_{v_s}$
, the following elements in
![]() $H$
:
$H$
:
If
![]() ${q}=1$
, before splitting, we have instead the following elements in
${q}=1$
, before splitting, we have instead the following elements in
![]() $H$
:
$H$
:
Hence, we let
![]() ${\ell }\,{:\!=}\,i_{r+1}$
and let
${\ell }\,{:\!=}\,i_{r+1}$
and let
![]() $c\in [2,d-2]\cup [d+1,s]$
be such that
$c\in [2,d-2]\cup [d+1,s]$
be such that
![]() $j_c={\ell }$
. We consider the
$j_c={\ell }$
. We consider the
![]() $\ell$
th projection of
$\ell$
th projection of
![]() $a_{\ell }a_{i_{r+2}}\cdots a_{i_{s-1}}a_0$
multiplied accordingly with that of
$a_{\ell }a_{i_{r+2}}\cdots a_{i_{s-1}}a_0$
multiplied accordingly with that of
![]() $a_j^{-1}a_{j_{d-2}}^{-1} \cdots a_{j_2}^{-1} a_k^{-1}$
or
$a_j^{-1}a_{j_{d-2}}^{-1} \cdots a_{j_2}^{-1} a_k^{-1}$
or
![]() $a_{j_s}^{-1} \cdots a_{j_{d+1}}^{-1} a_0$
. This is situation (ii).
$a_{j_s}^{-1} \cdots a_{j_{d+1}}^{-1} a_0$
. This is situation (ii).
Subcase (b): Suppose
![]() $r=1$
. Then we have the following elements in
$r=1$
. Then we have the following elements in
![]() $H$
:
$H$
:
If
![]() $i_2\ne j_1$
, let
$i_2\ne j_1$
, let
![]() $k\,{:\!=}\,{j_1}$
, and we proceed according to (ii), with
$k\,{:\!=}\,{j_1}$
, and we proceed according to (ii), with
![]() $\alpha$
being the
$\alpha$
being the
![]() $k$
th projection of
$k$
th projection of
![]() $a_ka_{j_2}\cdots a_{j_{d-2}}$
and
$a_ka_{j_2}\cdots a_{j_{d-2}}$
and
![]() $\beta$
that of
$\beta$
that of
![]() $( a_{i_{2}}\cdots a_{i_{s-1}}a_0)^{-1}$
. If
$( a_{i_{2}}\cdots a_{i_{s-1}}a_0)^{-1}$
. If
![]() $i_2= j_1$
, we let instead
$i_2= j_1$
, we let instead
![]() $k\,{:\!=}\,j_s$
and consider the
$k\,{:\!=}\,j_s$
and consider the
![]() $k$
th projection of
$k$
th projection of
![]() $(a_{i_{2}}\cdots a_{i_{s-1}}a_0)^{-1}$
multiplied with that of
$(a_{i_{2}}\cdots a_{i_{s-1}}a_0)^{-1}$
multiplied with that of
![]() $a_0^{-1}a_{j_{d+1}}\cdots a_{j_{s-1}}a_k$
; that is, situation (i).
$a_0^{-1}a_{j_{d+1}}\cdots a_{j_{s-1}}a_k$
; that is, situation (i).
Subcase (c): Suppose
![]() $r=s-1$
. Here we have the following elements in
$r=s-1$
. Here we have the following elements in
![]() $H$
:
$H$
:
If
![]() $i_1\ne j_1$
, we let
$i_1\ne j_1$
, we let
![]() $k\,{:\!=}\,{j_1}$
, and proceed as in (ii), taking
$k\,{:\!=}\,{j_1}$
, and proceed as in (ii), taking
![]() $\alpha$
to be the
$\alpha$
to be the
![]() $k$
th projection of
$k$
th projection of
![]() $a_ka_{j_2}\cdots a_{j_{d-2}}a_j$
and
$a_ka_{j_2}\cdots a_{j_{d-2}}a_j$
and
![]() $\beta$
that of
$\beta$
that of
![]() $( a_{i_{1}}\cdots a_{i_{s-2}}a_j)^{-1}$
. If
$( a_{i_{1}}\cdots a_{i_{s-2}}a_j)^{-1}$
. If
![]() $i_1= j_1$
, we instead let
$i_1= j_1$
, we instead let
![]() $k\,{:\!=}\,j_{d+1}$
and likewise following (ii) we consider the
$k\,{:\!=}\,j_{d+1}$
and likewise following (ii) we consider the
![]() $k$
th level projection of
$k$
th level projection of
![]() $ a_ka_{j_{d+2}}\cdots a_{j_s}$
multiplied with that of
$ a_ka_{j_{d+2}}\cdots a_{j_s}$
multiplied with that of
![]() $\big ( a_{i_1}\cdots a_{i_{s-2}}a_j \big )^{-1}$
.
$\big ( a_{i_1}\cdots a_{i_{s-2}}a_j \big )^{-1}$
.
We aim to continue in this manner, using newly formed parts of
![]() $g$
to split the existing parts of
$g$
to split the existing parts of
![]() $h_0$
, and then using the newly formed parts of
$h_0$
, and then using the newly formed parts of
![]() $h_0$
to split the existing parts of
$h_0$
to split the existing parts of
![]() $g$
. Observe also that if
$g$
. Observe also that if
![]() $a_i$
, for some
$a_i$
, for some
![]() $i\in [0,s-1]$
, is an isolated part of
$i\in [0,s-1]$
, is an isolated part of
![]() $g$
(i.e. a part of
$g$
(i.e. a part of
![]() $g$
of length one), then using (i) or (ii), one can further split the parts of
$g$
of length one), then using (i) or (ii), one can further split the parts of
![]() $h_0$
to isolate
$h_0$
to isolate
![]() $a_i$
from the parts of
$a_i$
from the parts of
![]() $h_0$
. Indeed, if
$h_0$
. Indeed, if
![]() $a_i$
or
$a_i$
or
![]() $a_i^{-1}$
occurs as an endpoint of a part of
$a_i^{-1}$
occurs as an endpoint of a part of
![]() $h_0$
, then it is clear. If
$h_0$
, then it is clear. If
![]() $a_i$
is an interior point of a part
$a_i$
is an interior point of a part
![]() $a_{r_1}\cdots a_{r_\xi } a_i a_{r_{\xi +1}}\cdots a_{r_{\xi +z}}$
of
$a_{r_1}\cdots a_{r_\xi } a_i a_{r_{\xi +1}}\cdots a_{r_{\xi +z}}$
of
![]() $h_0$
, then projecting to the
$h_0$
, then projecting to the
![]() $i$
th level, we have
$i$
th level, we have
and thus
are elements of
![]() $H_{v_{i+1}}$
, giving
$H_{v_{i+1}}$
, giving
in
![]() $H_{v_{i+s}}$
. As usual, we then replace
$H_{v_{i+s}}$
. As usual, we then replace
![]() $H$
with
$H$
with
![]() $H_{v_{i+s}}$
. We proceed similarly in the case when
$H_{v_{i+s}}$
. We proceed similarly in the case when
![]() $a_i^{-1}$
is an interior point in a part of
$a_i^{-1}$
is an interior point in a part of
![]() $h_0$
.
$h_0$
.
Hence, we may assume that the set of length one part of
![]() $g$
is equal to the set of length one part of
$g$
is equal to the set of length one part of
![]() $h_0$
. Equivalently, the set of parts of
$h_0$
. Equivalently, the set of parts of
![]() $g$
of length at least two involve the same generators that appear in the parts of
$g$
of length at least two involve the same generators that appear in the parts of
![]() $h_0$
of length at least two.
$h_0$
of length at least two.
If there are no parts of length at least two, then all generators have been isolated, and we are done, so assume otherwise. Suppose for now that the parts of
![]() $g$
of length at least two are labelled as follows:
$g$
of length at least two are labelled as follows:
for some
![]() $1\le \mu \lt s$
, and similarly for
$1\le \mu \lt s$
, and similarly for
![]() $h_0$
:
$h_0$
:
for some
![]() $1\le \nu \lt s$
, with
$1\le \nu \lt s$
, with
![]() $\gamma _j=1$
if
$\gamma _j=1$
if
![]() $j\in [1,s-1]$
and
$j\in [1,s-1]$
and
![]() $\gamma _j=-1$
if
$\gamma _j=-1$
if
![]() $j=0$
and similarly for
$j=0$
and similarly for
![]() $\lambda _j$
. Here
$\lambda _j$
. Here
![]() $*$
stands for unspecified elements in the alphabet
$*$
stands for unspecified elements in the alphabet
![]() $S$
. Write
$S$
. Write
for the set of ordered pairs of the so-called endpoint generators. If
![]() $a_0$
has not been isolated, it follows that the corresponding set
$a_0$
has not been isolated, it follows that the corresponding set
![]() $\mathcal{E}_{h_0}$
of endpoint generator pairs for
$\mathcal{E}_{h_0}$
of endpoint generator pairs for
![]() $h_0$
is of the form
$h_0$
is of the form
subject to reordering the parts of
![]() $h_0$
. Indeed, else we may separate the parts further using (i). Without loss of generality, write
$h_0$
. Indeed, else we may separate the parts further using (i). Without loss of generality, write
Note that if
we may proceed as in (i) or (ii), since then an endpoint from a part of
![]() $g$
is an interior point in a part of
$g$
is an interior point in a part of
![]() $h_0$
, or vice versa. Hence,
$h_0$
, or vice versa. Hence,
![]() $\mu =\nu$
and
$\mu =\nu$
and
Since
![]() $ \{p_2,\ldots,p_\mu \}$
has less elements than
$ \{p_2,\ldots,p_\mu \}$
has less elements than
![]() $\{e_1,\ldots,e_\mu \}$
, it follows that
$\{e_1,\ldots,e_\mu \}$
, it follows that
![]() $e_i\in \{ q_1,\ldots,q_{\mu }\}$
for some
$e_i\in \{ q_1,\ldots,q_{\mu }\}$
for some
![]() $i\in [1,\mu ]$
. Then, we proceed as in (ii). Hence, if
$i\in [1,\mu ]$
. Then, we proceed as in (ii). Hence, if
![]() $a_0$
is not an isolated part of
$a_0$
is not an isolated part of
![]() $g$
(equivalently of
$g$
(equivalently of
![]() $h_0$
), then we can continue splitting the parts of
$h_0$
), then we can continue splitting the parts of
![]() $g$
and
$g$
and
![]() $h_0$
.
$h_0$
.
So suppose now that
![]() $a_0$
has been isolated. As reasoned above, we have
$a_0$
has been isolated. As reasoned above, we have
and
with
Similarly, if
we proceed as in (ii). So we assume that
To proceed, we now consider the element
![]() $h_{e_1}$
defined at the beginning of the proof. Proceeding as in (i) and (ii), we use the parts of
$h_{e_1}$
defined at the beginning of the proof. Proceeding as in (i) and (ii), we use the parts of
![]() $g$
and
$g$
and
![]() $h_0$
to split
$h_0$
to split
![]() $h_{e_1}$
into parts, and if possible, we likewise use the parts of
$h_{e_1}$
into parts, and if possible, we likewise use the parts of
![]() $h_{e_1}$
to further split the parts of
$h_{e_1}$
to further split the parts of
![]() $g$
and
$g$
and
![]() $h_0$
. We claim that
$h_0$
. We claim that
![]() $a_{e_1}$
has been isolated through this process. Indeed, analogously to the considerations above for when
$a_{e_1}$
has been isolated through this process. Indeed, analogously to the considerations above for when
![]() $a_0$
was assumed to be an endpoint in
$a_0$
was assumed to be an endpoint in
![]() $\mathcal{E}_g$
, if we have
$\mathcal{E}_g$
, if we have
and
where here
![]() $\eta \ge \mu$
, and by abuse of notation, we still write
$\eta \ge \mu$
, and by abuse of notation, we still write
![]() $e_i$
for the left endpoints and
$e_i$
for the left endpoints and
![]() $f_i$
for the right endpoints for the parts of
$f_i$
for the right endpoints for the parts of
![]() $g$
. Then, as seen before, there is some
$g$
. Then, as seen before, there is some
![]() $f_i\in \{k_1,\ldots,k_{\eta }\}$
for
$f_i\in \{k_1,\ldots,k_{\eta }\}$
for
![]() $i\in [1,{\eta }]$
, and we can proceed as in (i) or (ii). If instead
$i\in [1,{\eta }]$
, and we can proceed as in (i) or (ii). If instead
![]() $ (a_{e_1}^{-1},a_{\ell _1})\in \mathcal{E}_{h_{e_1}}$
then we multiply the
$ (a_{e_1}^{-1},a_{\ell _1})\in \mathcal{E}_{h_{e_1}}$
then we multiply the
![]() $e_1$
th projection of
$e_1$
th projection of
![]() $a_{e_1}*\cdots *a_{f_1}$
with that of
$a_{e_1}*\cdots *a_{f_1}$
with that of
![]() $a_{e_1}^{-1}*\cdots *a_{\ell _1}$
as in (ii). Lastly, if
$a_{e_1}^{-1}*\cdots *a_{\ell _1}$
as in (ii). Lastly, if
![]() $a_{e_1}^{-1}$
is an interior point in
$a_{e_1}^{-1}$
is an interior point in
![]() $\mathcal{E}_{h_{e_1}}$
, then we proceed as in (ii). In other words, if
$\mathcal{E}_{h_{e_1}}$
, then we proceed as in (ii). In other words, if
![]() $a_{e_1}$
is not an isolated part of
$a_{e_1}$
is not an isolated part of
![]() $g$
(equivalently of
$g$
(equivalently of
![]() $h_0$
and of
$h_0$
and of
![]() $h_{e_1}$
), then we can always continue splitting.
$h_{e_1}$
), then we can always continue splitting.
By abuse of notation, we redefine
![]() $\mathcal{E}_g$
to be the new set of endpoint pairs, after this further splitting of the parts of
$\mathcal{E}_g$
to be the new set of endpoint pairs, after this further splitting of the parts of
![]() $g$
. If
$g$
. If
![]() $\mathcal{E}_g\ne \varnothing$
, pick a left endpoint
$\mathcal{E}_g\ne \varnothing$
, pick a left endpoint
![]() $a_e$
for some
$a_e$
for some
![]() ${(a_e,a_*)}\in \mathcal{E}_g$
. From working in a similar manner with the element
${(a_e,a_*)}\in \mathcal{E}_g$
. From working in a similar manner with the element
![]() $h_e$
, we can isolate
$h_e$
, we can isolate
![]() $a_e$
.
$a_e$
.
Proceeding in this manner, we will end up with all individual generators.
Case 2: Suppose
![]() $d=1$
. Thus we have
$d=1$
. Thus we have
Write
![]() $i\,{:\!=}\,i_1$
and let
$i\,{:\!=}\,i_1$
and let
![]() $r\in [2,s]$
be such that
$r\in [2,s]$
be such that
![]() $j_r=i$
. As in situation (ii), we consider instead the
$j_r=i$
. As in situation (ii), we consider instead the
![]() $i$
th projection of
$i$
th projection of
![]() $g$
multiplied with that of
$g$
multiplied with that of
![]() $h_0^{-1}$
. We now proceed as in Case 1 with the argument using the pairs of endpoints
$h_0^{-1}$
. We now proceed as in Case 1 with the argument using the pairs of endpoints
![]() $\mathcal{E}_g$
.
$\mathcal{E}_g$
.
Case 3: Suppose
![]() $d=s$
. Here we proceed first using (i) and then following the argument laid out in Case 1.
$d=s$
. Here we proceed first using (i) and then following the argument laid out in Case 1.
Remark 5.7.
For the case
![]() $t=0$
, as mentioned above it is entirely analogous as compared to the case
$t=0$
, as mentioned above it is entirely analogous as compared to the case
![]() $t\gt 0$
. Whenever we had applied situation (i) in the case of
$t\gt 0$
. Whenever we had applied situation (i) in the case of
![]() $t\gt 0$
, we now use situation (ii) in the case
$t\gt 0$
, we now use situation (ii) in the case
![]() $t=0$
. After the first splitting, whenever we consider new endpoints for the next splittings, where we had considered left endpoints in the case
$t=0$
. After the first splitting, whenever we consider new endpoints for the next splittings, where we had considered left endpoints in the case
![]() $t\gt 0$
, we consider right endpoints in the case
$t\gt 0$
, we consider right endpoints in the case
![]() $t=0$
, and vice versa.
$t=0$
, and vice versa.
Remark 5.8.
Akin to [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8, Proposition 6.6], one can show that the group
![]() $\mathfrak{K(v)}$
has a non-normal maximal subgroup of index
$\mathfrak{K(v)}$
has a non-normal maximal subgroup of index
![]() $q$
, for infinitely many primes
$q$
, for infinitely many primes
![]() $q$
. Indeed, the group
$q$
. Indeed, the group
![]() $\mathfrak{K(v)}$
has a proper quotient isomorphic to
$\mathfrak{K(v)}$
has a proper quotient isomorphic to
![]() $W_m(\mathbb{Z})$
, where for
$W_m(\mathbb{Z})$
, where for
![]() $\mathcal{G}$
a group and
$\mathcal{G}$
a group and
![]() $m\in \mathbb{N}_{\ge 2}$
, we write
$m\in \mathbb{N}_{\ge 2}$
, we write
![]() $W_m(\mathcal{G})$
for the wreath product of
$W_m(\mathcal{G})$
for the wreath product of
![]() $\mathcal{G}$
with a cyclic group of order
$\mathcal{G}$
with a cyclic group of order
![]() $m$
. Writing
$m$
. Writing
![]() $L=\psi ^{-1}(\mathfrak{K(v)}^{\prime}\times \cdots \times \mathfrak{K(v)}^{\prime})$
and
$L=\psi ^{-1}(\mathfrak{K(v)}^{\prime}\times \cdots \times \mathfrak{K(v)}^{\prime})$
and
![]() $N=L\langle a_0^m \rangle \trianglelefteq \mathfrak{K(v)}$
, analogous to [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8
, Lemma 6.4] we have that
$N=L\langle a_0^m \rangle \trianglelefteq \mathfrak{K(v)}$
, analogous to [Reference Di Domenico, Fernández-Alcober, Noce and Thillaisundaram8
, Lemma 6.4] we have that
![]() $\mathfrak{K(v)}/N\cong W_m(\mathbb{Z}^{s-1})$
, which has
$\mathfrak{K(v)}/N\cong W_m(\mathbb{Z}^{s-1})$
, which has
![]() $W_m(\mathbb{Z})$
as a quotient group; compare also Theorem
1.1
(iii).
$W_m(\mathbb{Z})$
as a quotient group; compare also Theorem
1.1
(iii).
Acknowledgements
We are grateful to the referee for their valuable comments and for suggesting the iterated monodromy groups, and we thank G. A. Fernández-Alcober and B. Klopsch for their helpful feedback.
Financial support
This research was partially conducted in the framework of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)-funded research training group GRK 2240: Algebro-Geometric Methods in Algebra, Arithmetic and Topology and by the DFG – Project-ID 491392403 – TRR 358. The second author thanks the Heinrich-Heine-University of Düsseldorf and Bielefeld University for their hospitality.
Competing interests
The authors declare none.