Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T18:55:01.010Z Has data issue: false hasContentIssue false
  • English
  • Français

The Mazur property and completeness in the space of Bochner-integrable functions L1(μ, X)

Published online by Cambridge University Press:  18 May 2009

G. Schlüchtermann
G. Schlüchtermann
Affiliation:
Mathematisches Institut der Ludwig-Maximilians Universität, Theresienstrasse 39, W-8000 München 2, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A locally convex space (E, 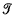) has the Mazur Property if and only if every linear 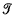-sequential continuous functional is 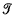-continuous (see [11]).

In the Banach space setting, a Banach space X is a Mazur space if and only if the dual space X* endowed with the w*-topology has the Mazur property. The Mazur property was introduced by S. Mazur, and, for Banach spaces, it is investigated in detail in [4], where relations with other properties and applications to measure theory are listed. T. Kappeler obtained (see [8]) certain results for the injective tensor product and showed that L1(μ, X), the space of Bochner-integrable functions over a finite and positive measure space (S, σ, μ), is a Mazur space provided X is also, and ℓ1 does not embed in X.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 2 , May 1992 , pp. 201 - 206
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Batt, J. and Hiermeyer, W., On compactness in L p (μ, X) in the weak topology and in the topology σL p (μ, X), L q (μ, X′) Math. Z. 182 (1983), 409–432.CrossRefGoogle Scholar
2.Diestel, J., Remarks on weak compactness in L 1(μ, X), Glasgow Math. J. 18 (1977), 87–91.CrossRefGoogle Scholar
3.Diestel, J. and Uhl, J. J. Jr, Vector measures, Mathematical Surveys No. 15 (American Mathematical Society, 1977).CrossRefGoogle Scholar
4.Edgar, G., Measurability in a Banach space, II, Indiana Univ. Math. J. 28 (1979), 559–579.CrossRefGoogle Scholar
5.Floret, K., Weakly compact sets, Lecture Notes in Mathematics 801 (Springer, 1980).CrossRefGoogle Scholar
6.Ghoussoub, N. and Saab, P., Weak compactness in spaces of Bochner integrable functions and the Radon–Nikodym property, Pacific J. Math. 110 (1984), 65–70.CrossRefGoogle Scholar
7.James, R. C., Weak compactness and reflexivity, Israel J. Math. 2 (1964), 101–119.CrossRefGoogle Scholar
8.Kappeler, T., Banach spaces with the condition of Mazur, Math. Z. 191 (1981), 623–631.CrossRefGoogle Scholar
9.Leung, D. H., On Banach Spaces with Mazur's property, Glasgow Math. J. 33 (1991), 51–54.CrossRefGoogle Scholar
10.Schlüchtermann, G. and Wheeler, R. F., On strongly WCG Banach spaces, Math. Z. 199 (1988), 387–398.CrossRefGoogle Scholar
11.Wilansky, A., Modern methods in topological vector spaces (McGraw-Hill, 1978).Google Scholar