Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mazo, J. E.
and
Odlyzko, A. M.
1990.
Lattice points in high-dimensional spheres.
Monatshefte für Mathematik,
Vol. 110,
Issue. 1,
p.
47.
Orlovskaya, E. V.
1997.
A minimum for the theta function in three variables and the solution of the Rankin-Sobolev problem in a three-dimensional space.
Journal of Mathematical Sciences,
Vol. 83,
Issue. 5,
p.
657.
Maeda, Yoshiaki
Rosenberg, Steven
and
Tondeur, Philippe
1997.
Minimal orbits of metrics.
Journal of Geometry and Physics,
Vol. 23,
Issue. 3-4,
p.
319.
Laugesen, Richard Snyder
and
Morpurgo, Carlo
1998.
Extremals for Eigenvalues of Laplacians under Conformal Mapping.
Journal of Functional Analysis,
Vol. 155,
Issue. 1,
p.
64.
Chua, Kok Seng
2000.
The height of the Leech lattice.
Bulletin of the Australian Mathematical Society,
Vol. 62,
Issue. 2,
p.
243.
El Soufi, Ahmad
and
Ilias, Saïd
2002.
Critical metrics of the trace of the heat kernel on a compact manifold.
Journal de Mathématiques Pures et Appliquées,
Vol. 81,
Issue. 10,
p.
1053.
Masser, D. W.
2003.
Sharp estimates for weierstrass elliptic functions.
Journal d'Analyse Mathématique,
Vol. 90,
Issue. 1,
p.
257.
Sarnak, Peter
and
Strömbergsson, Andreas
2006.
Minima of Epstein’s Zeta function and heights of flat tori.
Inventiones mathematicae,
Vol. 165,
Issue. 1,
p.
115.
Cohn, Henry
and
Kumar, Abhinav
2006.
Universally optimal distribution of points on spheres.
Journal of the American Mathematical Society,
Vol. 20,
Issue. 1,
p.
99.
Cohn, Henry
and
Kumar, Abhinav
2008.
Counterintuitive ground states in soft-core models.
Physical Review E,
Vol. 78,
Issue. 6,
Sandier, Etienne
and
Serfaty, Sylvia
2012.
From the Ginzburg-Landau Model to Vortex Lattice Problems.
Communications in Mathematical Physics,
Vol. 313,
Issue. 3,
p.
635.
Gruber, Peter M.
2012.
Application of an idea of Voronoĭ to lattice zeta functions.
Proceedings of the Steklov Institute of Mathematics,
Vol. 276,
Issue. 1,
p.
103.
Grabner, Peter J.
2014.
Applied Algebra and Number Theory.
p.
109.
Serfaty, Sylvia
2014.
Ginzburg-Landau Vortices, Coulomb Gases, and Renormalized Energies.
Journal of Statistical Physics,
Vol. 154,
Issue. 3,
p.
660.
Serfaty, Sylvia
2014.
Systems with Coulomb interactions.
Journées équations aux dérivées partielles,
p.
1.
Osting, Braxton
Marzuola, Jeremy
and
Cherkaev, Elena
2015.
An isoperimetric inequality for an integral operator on flat tori.
Illinois Journal of Mathematics,
Vol. 59,
Issue. 3,
Bétermin, Laurent
and
Zhang, Peng
2015.
Minimization of energy per particle among Bravais lattices in ℝ2: Lennard–Jones and Thomas–Fermi cases.
Communications in Contemporary Mathematics,
Vol. 17,
Issue. 06,
p.
1450049.
Zhang, Peng
2015.
On the minimizer of a renormalized energy related to the Ginzburg–Landau model.
Comptes Rendus. Mathématique,
Vol. 353,
Issue. 3,
p.
255.
Brauchart, Johann S.
and
Grabner, Peter J.
2015.
Distributing many points on spheres: Minimal energy and designs.
Journal of Complexity,
Vol. 31,
Issue. 3,
p.
293.
Bétermin, Laurent
2016.
Two-Dimensional Theta Functions and Crystallization among Bravais Lattices.
SIAM Journal on Mathematical Analysis,
Vol. 48,
Issue. 5,
p.
3236.

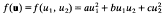 be a positive definite binary quadratic form with real coefficients and discriminant
be a positive definite binary quadratic form with real coefficients and discriminant 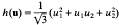 . The Epstein zeta function of
. The Epstein zeta function of