Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T14:36:25.339Z Has data issue: false hasContentIssue false
  • English
  • Français

A Minimum Problem for the Epstein Zeta-Function

Published online by Cambridge University Press:  18 May 2009

R. A. Rankin
R. A. Rankin
Affiliation:
The University, Birmingham, 15
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

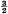In some recent work by D. G. Kendall and the author † on the number of points of a lattice which lie in a random circle the mean value of the variance emerged as a constant multiple of the value of the Epstein zeta-function Z(s) associated with the lattice, taken at the point s=. Because of the connexion with the problems of closest packing and covering it seemed likely that the minimum value of Z(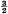) would be attained for the hexagonal lattice; it is the purpose of this paper to prove this and to extend the result to other real values of the variable s.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 1 , Issue 4 , December 1953 , pp. 149 - 158
Copyright
Copyright © Glasgow Mathematical Journal Trust 1953

References

† “On the number of points of a given lattice in a random hypersphere.” (To appear in the Quarterly Journal.)

‡ For the general theory of Zh(s) see Deuring, Max, “Zetafunktionen quadratischer Formen” J. reine angew. Math. 172 (1935), 226–252.Google Scholar

† Deuring (loc. cit.) gives a somewhat similar formula for the function G (x, y), but with a different form of remainder and without the explicit numerical constants which are essential for our purpose.

† Cambridge, 1922.

† “On the number of lattice points inside a random oval,” Quart. J. Math., Oxford Ser. 19 (1948), 1–26.Google Scholar