Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T04:43:48.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed Hilbert modular forms and families of abelian varieties

Published online by Cambridge University Press:  18 May 2009

Min Ho Lee
Min Ho Lee
Affiliation:
Department of Mathematics, University of Northern Iowa, Cedar Falls, IA 50614, U.S.A. E-mail address: lee@math.uni.edu
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [18] Shioda proved that the space of holomorphic 2-forms on a certain type of elliptic surface is canonically isomorphic to the space of modular forms of weight three for the associated Fuchsian group. Later, Hunt and Meyer [6] made an observation that the holomorphic 2-forms on a more general elliptic surface should in fact be identified with mixed automorphic forms associated to an automorphy factor of the form

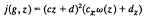
for z in the Poincaré upper half plane ℋ, g = 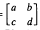and χ(g) = 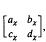, where g is an element of the fundamental group Γ⊂PSL(2, R) of the base space of the elliptic fibration, χ-Γ→SL(2, R) the monodromy representation, and w: ℋ→ℋ the lifting of the period map of the elliptic surface.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 2 , May 1997 , pp. 131 - 140
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Ash, A., Mumford, D., Rapoport, M. and Tai, Y., Smooth compactification of locally symmetric varieties. Lie groups: history, frontiers and applications IV, (Math. Sci. Press, 1975).Google Scholar
2.Baily, W. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains, Ann. of Math. 84 (1966), 442–528.CrossRefGoogle Scholar
3.Deligne, P., Variétés de Shimura: interpretation modulaire, et techniques de construction de modèles canoniques, Proc. Sympos. Pure Math. 33 (1979), 247–290.Google Scholar
4.Harris, M., Functorial properties of toroidal compactification of locally symmetric varieties, Proc. London Math. Soc. (3) 59 (1989), 1–22.CrossRefGoogle Scholar
5.Harris, M., Automorphic forms of δ-cohomology type as coherent cohomology classes, J. Differential Geom. 32 (1990), 1–63.Google Scholar
6.Hunt, B. and Meyer, W., Mixed automorphic forms and invariants of elliptic surfaces, Math. Ann. 271 (1985), 53–80.CrossRefGoogle Scholar
7.Kuga, M., Fiber varieties over a symmetric space whose fibers are abelian varieties I, II, Lect. Notes, Univ. Chicago (1963/1964).Google Scholar
8.Lee, M. H., Mixed cusp forms and holomorphic forms on elliptic varieties, Pacific J. Math. 132 (1988), 363–370.Google Scholar
9.Lee, M. H., Conjugates of equivariant holomorphic maps of symmetric domains, Pacific J. Math. 149 (1991), 127–144.Google Scholar
10.Lee, M. H., Mixed cusp forms and Poincare' series, Rocky Mountain J. Math. 23 (1993), 1009–1022.CrossRefGoogle Scholar
11.Lee, M. H., Mixed Siegel modular forms and Kuga fiber varieties, Illinois J. Math. 38 (1994), 692–700.CrossRefGoogle Scholar
12.Lee, M. H., Mixed automorphic vector bundles on Shimura varieties, Pacific J. Math. 173 (1996), 105–126.CrossRefGoogle Scholar
13.Lee, M. H., Hodge cycles on Kuga fiber varieties, J. Austral. Math. Soc. Ser. A 61 (1996), 1–13.CrossRefGoogle Scholar
14.Manin, Y., Non-archimedian integration and Jacquet-Langlands p-adic L-functions, Russian Math. Surveys 31 (1976), 5–57.Google Scholar
15.Milne, J., Canonical models of (mixed) Shimura varieties and automorphic vector bundles, Automorphic forms, Shimura varieties, and L-functions, vol. I (Academic Press, 1990), 283–414.Google Scholar
16.Pink, R., Arithmetical compactification of mixed Shimura varieties, Bonner Math. Schriften, 209 (Universität Bonn, 1990).Google Scholar
17.Satake, I., Algebraic structures of symmetric domains (Princeton Univ. Press, 1980).Google Scholar
18.Shioda, T., On elliptic modular surfaces, J. Math. Soc. Japan 24 (1972), 20–59.CrossRefGoogle Scholar