Hostname: page-component-6bf8c574d5-n2sc8 Total loading time: 0 Render date: 2025-03-07T02:56:44.375Z Has data issue: false hasContentIssue false
  • English
  • Français

The modularity of the lattice of varieties of completely regular semigroups and related representations

Published online by Cambridge University Press:  18 May 2009

Mario Petrich  and
Norman R. Reilly
Mario Petrich
Affiliation:
Simon Fraser University, Burnaby, B.C., Canada.
Norman R. Reilly
Affiliation:
Simon Fraser University, Burnaby, B.C., Canada.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A semigroup endowed with a unary operation satisfying the identities

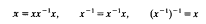
is a completely regular semigroup. In several recent papers devoted to the study of the lattice 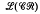of subvarieties of the variety 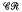of completely regular semigroups, various results have been obtained which decompose special intervals in 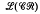into either direct products or subdirect products. Petrich [14], Hall and Jones [6] and Rasin [20] have shown that certain intervals of the form 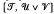, where 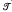is the trivial variety and 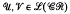are subdirect products of 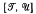and 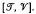Pastijn and Trotter [13] show that certain intervals of the form 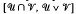are direct products of the intervals 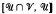and 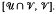The main objective of this paper is to develop an appropriate lattice theoretic framework for these representations.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 2 , May 1990 , pp. 137 - 152
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Birkhoff, G., Lattice Theory, Amer. Math. Soc. Colloq. Publ. Vol. XXV, Providence, 1964.Google Scholar
2.Burris, S. and Nelson, E., Embedding the dual of nm in the lattice of equational classes of commutative semigroups, Proc. Amer. Math. Soc. 30 (1971), 37–39.Google Scholar
3.Clifford, A. H., The free completely regular semigroup on a set, J. Algebra 59 (1979), 434–451.Google Scholar
4.Feigenbaum, R., Regular semigroup congruences, Semigroup Forum 17 (1979), 371–377.CrossRefGoogle Scholar
5.Gratzer, G., General lattice theory, (Academic Press 1978).CrossRefGoogle Scholar
6.Hall, T. E. and Jones, P. R., On the lattice of varieties of bands of groups, Pacific J. Math. 91 (1980), 327–337.Google Scholar
7.Higman, G., Representations of general linear groups and varieties of p-groups, Proc. Int. Conf. on the Theory of Groups, Gordon and Breach, New York (1967), 167–173.Google Scholar
8.Howie, J. M., An Introduction to Semigroup Theory, (Academic Press, 1976).Google Scholar
9.Jones, P. R., On the lattice of varieties of completely regular semigroups, J. Austral. Math. Soc. A35 (1983), 227–235.CrossRefGoogle Scholar
10.Jones, P. R., Mal'cev products of varieties of completely regular semigroups, J. Austral. Math. Soc. A42 (1987), 227–246.CrossRefGoogle Scholar
11.Pastijn, F., The lattice of completely regular semigroup varieties (preprint).Google Scholar
12.Pastijn, F. and Petrich, M., Congruences on regular semigroups, Trans. Amer. Math. Soc. 295 (1986), 607–633.CrossRefGoogle Scholar
13.Pastijn, F. and Trotter, P. G., Lattices of completely regular semigroup varieties, Pacific J. Math. 119 (1985), 191–214.CrossRefGoogle Scholar
14.Petrich, M., Varieties of orthodox bands of groups, Pacific J. Math. 58 (1975), 209–217.Google Scholar
15.Petrich, M., Inverse Semigroups, (Wiley Interscience, 1984).Google Scholar
16.Petrich, M. and Reilly, N. R., Semigroups generated by certain operators on varieties of completely regular semigroups, Pacific J. Math. 132 (1988), 151–175.Google Scholar
17.Polák, L., On varieties of completely regular semigroups I, Semigroup Forum 32 (1985), 97–123.Google Scholar
18.Polák, L., On varieties of completely regular semigroups II, Semigroup Forum 36 (1987), 253–284.CrossRefGoogle Scholar
19.Rasin, V. V., Free completely simple semigroups, Ural. Gos. Univ. Mat. Zap. 11 (1979), 140–151 (Russian).Google Scholar
20.Rasin, V. V., On the varieties of Cliffordian semigroups, Semigroup Forum 23 (1981), 201–220.CrossRefGoogle Scholar
21.Reilly, N. R., Varieties of completely regular semigroups, J. Austral. Math. Soc. A38 (1985), 372–393.Google Scholar