Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:09:47.419Z Has data issue: false hasContentIssue false
  • English
  • Français

The nonclassical diffusion equations with time-dependent memory kernels and a new class of nonlinearities

Part of: Partial differential equations Diffusion and convection Representations of solutions

Published online by Cambridge University Press:  21 February 2022

Le Thi Thuy  and
Nguyen Duong Toan
Le Thi Thuy
Affiliation:
Department of Mathematics, Electric Power University, 235 Hoang Quoc Viet, Tu Liem, Hanoi, Vietnam e-mail: thuylephuong@gmail.com
Nguyen Duong Toan
Affiliation:
Faculty of Mathematics and Natural Sciences, Haiphong University, 171 Phan Dang Luu, Kien An, Haiphong, Vietnam e-mail: toannd@dhhp.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, we consider the nonclassical diffusion equations with time-dependent memory kernels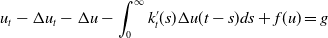

\begin{equation*} u_{t} - \Delta u_t - \Delta u - \int_0^\infty k^{\prime}_{t}(s) \Delta u(t-s) ds + f( u) = g \end{equation*}
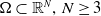on a bounded domain $\Omega \subset \mathbb{R}^N,\, N\geq 3$ . Firstly, we study the existence and uniqueness of weak solutions and then, we investigate the existence of the time-dependent global attractors 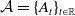$\mathcal{A}=\{A_t\}_{t\in\mathbb{R}}$ in 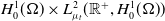$H_0^1(\Omega)\times L^2_{\mu_t}(\mathbb{R}^+,H_0^1(\Omega))$ . Finally, we prove that the asymptotic dynamics of our problem, when 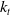$k_t$ approaches a multiple 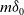$m\delta_0$ of the Dirac mass at zero as 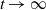$t\to \infty$ , is close to the one of its formal limit
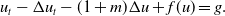\begin{equation*}u_{t} - \Delta u_{t} - (1+m)\Delta u + f( u) = g. \end{equation*}
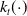The main novelty of our results is that no restriction on the upper growth of the nonlinearity is imposed and the memory kernel $k_t(\!\cdot\!)$ depends on time, which allows for instance to describe the dynamics of aging materials.

MSC classification

Primary: 35B41: Attractors 35D30: Weak solutions 76R50: Diffusion
Secondary: 45K05: Integro-partial differential equations
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 3 , September 2022 , pp. 716 - 733
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aifantis, E. C., On the problem of diffusion in solids, Acta Mech. 37 (1980), 265–296.CrossRefGoogle Scholar
Anh, C. T. and Bao, T. Q., Pullback attractors for a class of non-autonomous nonclassical diffusion equations, Nonlinear Anal. 73 (2010), 399–412.CrossRefGoogle Scholar
Anh, C. T. and Toan, N. D., Existence and upper semicontinuity of uniform attractors in $H^1(\mathbb{R}^N)$ for non-autonomous nonclassical diffusion equations, Ann. Polon. Math. 113 (2014), 271–295.CrossRefGoogle Scholar
Anh, C. T. and Toan, N. D., Nonclassical diffusion equations on $\mathbb R^N$ with singular oscillating external forces, Appl. Math. Lett. 38 (2014), 20–26.CrossRefGoogle Scholar
Anh, C. T., Thanh, D. T. P. and Toan, N. D., Global attractors for nonclassical diffusion equations with hereditary memory and a new class of nonlinearities, Ann. Polon. Math. 119 (2017), 1–21.CrossRefGoogle Scholar
Anh, C. T., Thanh, D. T. P. and Toan, N. D., Averaging of noncassical diffusion equations with memory and singularly oscillating forces, Z. Anal. Anwend. 37 (2018), 299–314.CrossRefGoogle Scholar
Conti, M., Danese, V. and Pata, V., Viscoelasticity with time-dependent memory kernels. Part II: Asymptotic behavior of solutions, Am. J. Math. 140 (2018), 1687–1179.Google Scholar
Conti, M., Danese, V., Giorgi, C. and Pata, V., A model of viscoelasticity with time-dependent memory kernels, Am. J. Math. V140(2) (2018), 349–389.CrossRefGoogle Scholar
Conti, M., Marchini, E. M. and Pata, V., Nonclassical diffusion with memory, Math. Meth. Appl. Sci. 38 (2015), 948–958.CrossRefGoogle Scholar
Conti, M., Pata, V. and Temam, R., Attractors for processes on time-dependent spaces. Applications to wave equations, J. Differ. Equations 255 (2013), 1254–1277.CrossRefGoogle Scholar
Conti, M. and Pata, V., Asymptotic structure of the attractor for processes on time-dependent spaces, Nonlinear Anal. Real World Appl. 19 (2014), 1–10.CrossRefGoogle Scholar
Dafermos, C. M., Asymptotic stability in viscoelasticity, Arch. Rational Mech. Anal. 37 (1970), 297–308.CrossRefGoogle Scholar
Di Plinio, F., Duane, G. S. and Temam, R., Time dependent attractor for the oscillon equation, Discrete Contin. Dyn. Syst. 29 (2011), 141–167.CrossRefGoogle Scholar
Geredeli, P. G., On the existence of regular global attractor for p-Laplacian evolution equation, Appl. Math. Optim. 71 (2015), 517–532.CrossRefGoogle Scholar
Geredeli, P. G. and Khanmamedov, A., Long-time dynamics of the parabolic p-Laplacian equation, Commun. Pure Appl. Anal. 12 (2013), 735–754.CrossRefGoogle Scholar
Jäkle, J., Heat conduction and relaxation in liquids of high viscosity, Physica A Stat. Mech. Appl. 162 (1990), 377–404.CrossRefGoogle Scholar
Krasnoselskii, M., Zabreiko, P., Pustylnik, E. and Sobolevskii, P., Integral operators in spaces of summable functions (Noordhoff, Leyden, 1976).CrossRefGoogle Scholar
Lions, J.-L., Quelques Méthodes de Résolution des Problèmes aux Limites Non Linéaires (Dunod, Paris, 1969).Google Scholar
Liu, Y., Time-dependent global attractor for the nonclassical diffusion equations, Appl. Anal. 94 (2015), 1439–1449.Google Scholar
Liu, Y. and Ma, Q., Exponential attractors for a nonclassical diffusion equation, Electron. J. Differ. Equa. 2009(9) (2009), 1–7.Google Scholar
Ma, Q., Wang, X. and Xu, L., Existence and regularity of time-dependent global attractors for the nonclassical reaction-diffusion equations with lower forcing term, Bound. Value Probl. (2016), Paper No. 10, 11 pp.Google Scholar
Peter, J. C. and Gurtin, M. E., On a theory of heat conduction involving two temperatures, Z. Angew. Math. Phys. 19 (1968), 614–627.Google Scholar
Simon, J., Compact sets in the space $L^p(0, T; B)$ , Annali Mat. Pura Appl. 146 (1987), 65–96.CrossRefGoogle Scholar
Sun, C., Wang, S. and Zhong, C. K., Global attractors for a nonclassical diffusion equation, Acta Math. Appl. Sin. Engl. Ser. 23 (2007), 1271–1280.CrossRefGoogle Scholar
Sun, C. and Yang, M., Dynamics of the nonclassical diffusion equations, Asymptot. Anal. 59 (2009), 51–81.Google Scholar
Toan, N. D., Existence and long-time behavior of variational solutions to a class of nonclassical diffusion equations in non-cylindrical domains, Acta Math. Vietnam 41 (2016), 37–53.CrossRefGoogle Scholar
Truesdell, C. and Noll, W., The nonlinear field theories of mechanics, Encyclomedia of Physics (Springer, Berlin, 1995).Google Scholar
Wang, S., Li, D. and Zhong, C. K., On the dynamics of a class of nonclassical parabolic equations, J. Math. Anal. Appl. 317 (2006), 565–582.CrossRefGoogle Scholar
Wang, X., Yang, L. and Zhong, C. K., Attractors for the nonclassical diffusion equations with fading memory, J. Math. Anal. Appl. 362 (2010), 327–337.CrossRefGoogle Scholar
Wang, X. and Zhong, C. K., Attractors for the non-autonomous nonclassical diffusion equations with fading memory, Nonlinear Anal. 71 (2009), 5733–5746.CrossRefGoogle Scholar
Xiao, Y., Attractors for a nonclassical diffusion equation, Acta Math. Appl. Sin. Engl. Ser. 18 (2002), 273–276.CrossRefGoogle Scholar
Xie, Y., Li, Q. and Zhu, K., Attractors for nonclassical diffusion equations with arbitrary polynomial growth nonlinearity, Nonlinear Anal. Real World Appl. 31 (2016), 23–37.CrossRefGoogle Scholar
Zhang, F. and Liu, Y., Pullback attractors in $${H^1}({\mathbb{R}^N})$$ for non-autonomous nonclassical diffusion equations, Dyn. Syst. 29 (2014), 106–118.CrossRefGoogle Scholar