Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mena, J.F
Payá, R
Rodríguez, A
and
Yost, D.T
1991.
Absolutely proximinal subspaces of Banach spaces.
Journal of Approximation Theory,
Vol. 65,
Issue. 1,
p.
46.
Contreras, Manuel D.
and
Payá, Rafael
1994.
On upper semicontinuity of duality mappings.
Proceedings of the American Mathematical Society,
Vol. 121,
Issue. 2,
p.
451.
Giles, J. R.
and
Moors, W. B.
1996.
Generic continuity of restricted weak upper semi-continuous set-valued mappings.
Set-Valued Analysis,
Vol. 4,
Issue. 1,
p.
25.
Guerrero, Julio Becerra
and
Palacios, Angel Rodriguez
2000.
Isometric Reflections on Banach Spaces after a Paper of A. Skorik and M. Zaidenberg.
Rocky Mountain Journal of Mathematics,
Vol. 30,
Issue. 1,
Benítez, Julio
and
Montesinos, Vicente
2001.
Restricted weak upper semicontinuous differentials of convex functions.
Bulletin of the Australian Mathematical Society,
Vol. 63,
Issue. 1,
p.
93.
Amin, Kaidi El
Campoy, Antonio Morales
and
Palacios, Angel Rodriguez
2001.
Geometrical Properties of the Product of a $C^*$-Algebra.
Rocky Mountain Journal of Mathematics,
Vol. 31,
Issue. 1,
Palacios, Ángel Rodríguez
2010.
Banach space characterizations of unitaries: A survey.
Journal of Mathematical Analysis and Applications,
Vol. 369,
Issue. 1,
p.
168.
Moreno Galindo, Antonio
and
Rodríguez Palacios, Ángel
2010.
On multiplicatively closed subsets of normed algebras.
Journal of Algebra,
Vol. 323,
Issue. 5,
p.
1530.
Acosta, María D.
Becerra Guerrero, Julio
and
Rodríguez-Palacios, Angel
2011.
Weakly open sets in the unit ball of the projective tensor product of Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 383,
Issue. 2,
p.
461.
Cobollo, Christian
Dantas, Sheldon
Hájek, Petr
and
Jung, Mingu
2025.
On the strongly subdifferentiable points in Lipschitz-free spaces.
Banach Journal of Mathematical Analysis,
Vol. 19,
Issue. 1,

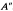 of a unital Banach algebra
of a unital Banach algebra 