Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shaw, Sen-Yen
1984.
On numerical ranges of generalized derivations and related properties.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 36,
Issue. 1,
p.
134.
Duggal, B.P.
2004.
Subspace gaps and range-kernel orthogonality of an elementary operator.
Linear Algebra and its Applications,
Vol. 383,
Issue. ,
p.
93.
Harte, Robin
and
Larson, David
2004.
Skew exactness perturbation.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 9,
p.
2603.
Harte, Robin
2005.
Skew exactness and range-kernel orthogonality.
Filomat,
p.
19.
Duggal, B.
2005.
A perturbed elementary operator and range-kernel orthogonality.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 6,
p.
1727.
Harte, Robin
2008.
Skew exactness and range-kernel orthogonality II.
Journal of Mathematical Analysis and Applications,
Vol. 347,
Issue. 1,
p.
370.
Segres, A.
and
Bachir, A.
2009.
Fuglede and elementary operators on Banach space.
Filomat,
Vol. 23,
Issue. 3,
p.
125.
Boasso, Enrico
and
Rakocevic, Vladimir
2011.
Characterizations of EP and normal Banach algebra elements and Banach space operators.
Linear Algebra and its Applications,
Vol. 435,
Issue. 2,
p.
342.
Turnšek, Aleksej
2017.
Fuglede Putnam theorem in Banach algebras.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 5,
p.
937.
Mortad, Mohammed Hichem
2022.
The Fuglede-Putnam Theory.
Vol. 2322,
Issue. ,
p.
43.
Kissin, E.
Potapov, D.
Shulman, V.
and
Sukochev, F.
2025.
Operator–Lipschitz functions on symmetrically normed ideals with nontrivial Boyd indices.
Journal of the London Mathematical Society,
Vol. 112,
Issue. 1,

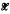 is said to be hermitian if ∥exp(
is said to be hermitian if ∥exp(