Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:02:14.083Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on integral equations

Published online by Cambridge University Press:  18 May 2009

W. E. Williams
W. E. Williams
Affiliation:
University of Surrey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper Cooke [1] obtained a solution of the integral equation

by using the identity

and the technique, first used by Copson, of interchanging the orders of integration and hence reducing the problem to that of the successive solution of two Abel integral equations. It is also shown in [1] that the above identity can also be used to solve the dual series equations

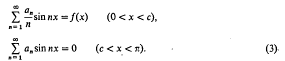
The kernel in equation (1) is a particular member of a general class of kernels which the author [6] has shown to be such that the resulting integral equation is directly soluble by using Copson's technique. The particular example of equation (1) is given in [6] and the identity of equation (2) was used by the author [7] to obtain the solution of equation (3).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 13 , Issue 2 , September 1972 , pp. 119 - 121
Copyright
Copyright © Glasgow Mathematical Journal Trust 1972

References

REFERENCES

1.Cooke, J. C., The solution of some integral equations and their connection with dual integral equations and series, Glasgow Math. J. 11 (1970), 9–20.CrossRefGoogle Scholar
2.Lundgren, T. and Chiang, D., Solution of a class of singular integral equations, Quart. Appl. Math. 24 (1967), 303–313.CrossRefGoogle Scholar
3.Peters, A. S., A note on the integral equation of the first kind with a Cauchy kernel, Comm. Pure App. Math. 16 (1963), 57–61.CrossRefGoogle Scholar
4.Peters, A. S., Abel's equation and the Cauchy integral equation of the second kind, Comm. Pure App. Math. 21 (1968), 51–65.CrossRefGoogle Scholar
5.Peters, A. S., Some integral equations related to Abel's equation and the Hilbert transform, Comm. Pure App. Math. 22 (1969), 539–560.CrossRefGoogle Scholar
6.Williams, W. E., A class of integral equations, Proc. Cambridge Philos. Soc. 59 (1963), 589–597.CrossRefGoogle Scholar
7.Williams, W. E., The solution of dual series and dual integral equations, Proc. Glasgow Math. Assoc. 6 (1964), 123–129.CrossRefGoogle Scholar