Hostname: page-component-7f64f4797f-kjzhn Total loading time: 0 Render date: 2025-11-04T16:08:36.068Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE CONNECTEDNESS OF THE BRANCH LOCUS OF RATIONAL MAPS

Published online by Cambridge University Press:  20 March 2017

RUBEN A. HIDALGO  and
SAÚL QUISPE
RUBEN A. HIDALGO
Affiliation:
Departamento de Matemática y Estadística, Universidad de La Frontera. Casilla 54-D, 4780000 Temuco, Chile e-mails: ruben.hidalgo@ufrontera.cl, saul.quispe@ufrontera.cl
SAÚL QUISPE
Affiliation:
Departamento de Matemática y Estadística, Universidad de La Frontera. Casilla 54-D, 4780000 Temuco, Chile e-mails: ruben.hidalgo@ufrontera.cl, saul.quispe@ufrontera.cl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Milnor proved that the moduli space Md of rational maps of degree d ≥ 2 has a complex orbifold structure of dimension 2(d − 1). Let us denote by 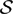${\mathcal S}$ d the singular locus of Md and by 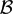${\mathcal B}$ d the branch locus, that is, the equivalence classes of rational maps with non-trivial holomorphic automorphisms. Milnor observed that we may identify M2 with ℂ2 and, within that identification, that 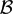${\mathcal B}$ 2 is a cubic curve; so 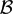${\mathcal B}$ 2 is connected and 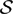${\mathcal S}$ 2 = ∅. If d ≥ 3, then it is well known that 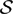${\mathcal S}$ d = 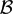${\mathcal B}$ d . In this paper, we use simple arguments to prove the connectivity of 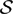${\mathcal S}$ d .

Keywords

37F10

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 1 , January 2018 , pp. 199 - 207
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Bartolini, G., Costa, A. F. and Izquierdo, M., On the connectivity of branch loci of moduli spaces, Ann. Acad. Sci. Fenn. 38 (1) (2013), 245–258.Google Scholar
2. Beardon, A. F., The geometry of discrete groups. Corrected reprint of the 1983 original. Graduate Texts in Mathematics, vol. 91 (Springer-Verlag, New York, 1995), xii+337, ISBN: 0-387-90788-2.Google Scholar
3. Doyle, P. and McMullen, C., Solving the quintic by iteration, Acta Math. 163 (1989), 151–180.CrossRefGoogle Scholar
4. Fujimura, M., Singular parts of moduli spaces for cubic polynomials and quadratic rational maps, RIMS Kokyuroku 986 (1997), 57–65.Google Scholar
5. Hidalgo, R. A. and Izquierdo, M., On the connectivity of the branch locus of the Schottky space, Ann. Acad. Sci. Fenn. 3 (2014), 635–654.Google Scholar
6. Levy, A., The space of morphisms on projective space, Acta Arith. 146 (1) (2011), 13–31.Google Scholar
7. Miasnikov, N., Stout, B. and Williams, Ph., Automorphism loci for the moduli space of rational maps, https://arxiv.org/pdf/1408.5655v2.pdf 12 Sep 2014.Google Scholar
8. Manes, M., Moduli spaces for families of rational maps on ℙ1 , J. Number Theory 129 (2009), 1623–1663.CrossRefGoogle Scholar
9. Milnor, J., Geometry and dynamics of quadratic rational maps, with an appendix by the author and Lei Tan, Experiment. Math. 2 (1993), 37–83.Google Scholar
10. Silverman, J. H., The space of rational maps on ℙ1 , Duke Math. J. 94 (1998), 41–77.Google Scholar
11. Sullivan, D., Quasiconformal homeomorphisms and dynamics I. Solution of the Fatou-Julia problem on wandering domains, Ann. Math. 122 (2) (1985), 401–418.Google Scholar