Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T07:01:39.718Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE GENUS OF GLOBAL FUNCTION FIELDS

Published online by Cambridge University Press:  26 February 2013

ZHENGJUN ZHAO  and
XIA WU
ZHENGJUN ZHAO
Affiliation:
School of Mathematics and Computational Science, AnQing Normal University, AnQing 246133, People's Republic of China e-mail: zywnju@gmail.com
XIA WU*
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, People's Republic of China e-mail: xiaxia80@gmail.com
*
*Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To give a relatively elementary proof of the Brumer–Stark conjecture in a function field context involving no algebraic geometry beyond the Riemann–Roch theorem for curves, Hayes Compos. Math., vol. 55, 1985, pp. 209–239) defined a normalizing field 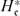$H_\mathfrak{e}^*$ associated with a fixed sgn-normalized Drinfeld module and its extension field 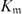$K_\mathfrak{m}$, which is an analogue of cyclotomic function fields over a rational function field. We present explicitly in this note the formulae for the genus of the two fields and the maximal real subfield 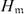$H_\mathfrak{m}$ of 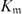$K_\mathfrak{m}$. In some sense, our results can be regarded as generalizations of formulae for the genus of classical cyclotomic function fields obtained by Hayes Trans. Amer. Math. Soc., vol. 189, 1974, pp. 77–91) and Kida and Murabayashi (Tokyo J. Math., vol. 14(1), 1991, pp. 45–56).

Keywords

11R5811R6011G09
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 3 , September 2013 , pp. 559 - 565
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Hayes, D., Explicit class field theory for rational function fields, Trans. Amer. Math. Soc. 189 (1974), 77–91.Google Scholar
2.Hayes, D., Explicit class field theory in global function fields, Studies in Algebra and Number Theory, Adv. Math. Supplementary Studies 6 (1979), 173–217.Google Scholar
3.Hayes, D., Analytic class number formulas in global function fields, Invent. Math. 65 (1981), 49–69.CrossRefGoogle Scholar
4.Hayes, D., Stickelberger elements in function fields, Compos. Math. 55 (1985), 209–239.Google Scholar
5.Kida, M. and Murabayashi, N., Cyclotomic function fields with divisor class number one, Tokyo J. Math. 14 (1) (1991), 45–56.Google Scholar
6.Rosen, M., Number theory in function fields, Graduate Texts in Mathematics, vol. 210 (Springer, Berlin, 2002).CrossRefGoogle Scholar