No CrossRef data available.
Article contents
A note on the rational homological dimension of lattices in positive characteristic
Part of:
Special aspects of infinite or finite groups
Connections with homological algebra and category theory
Published online by Cambridge University Press: 10 June 2022
Abstract
We show via 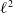 $\ell^2$-homology that the rational homological dimension of a lattice in a product of simple simply connected Chevalley groups over global function fields is equal to the rational cohomological dimension and to the dimension of the associated Bruhat–Tits building.
$\ell^2$-homology that the rational homological dimension of a lattice in a product of simple simply connected Chevalley groups over global function fields is equal to the rational cohomological dimension and to the dimension of the associated Bruhat–Tits building.
MSC classification
Primary:
20J06: Cohomology of groups
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Davis, M. W. et al., Weighted L2-cohomology of Coxeter groups, Geom.
Topol. 11 (2007), 47–138. ISSN: 1465-3060. doi: 10.2140/gt.2007.11.47.Google Scholar
Dymara, J., L2-cohomology of buildings with fundamental class, Proc. Amer. Math. Soc. 132(6) (2004), 1839–1843. ISSN: 0002-9939. doi: 10.1090/S0002-9939-03-07234-4.CrossRefGoogle Scholar
Dymara, J., Thin buildings, Geom. Topol. 10 (2006), 667–694. ISSN: 1465-3060. doi: 10.2140/gt.2006.10.667.CrossRefGoogle Scholar
Gaboriau, D., Invariants l2 de relations d’Équivalence et de groupes, Publ. Math. Inst. Hautes Études Sci. 95 (2002), 93–150. ISSN: 0073-8301. doi: 10.1007/s102400200002.Google Scholar
Gandini, G., Bounding the homological finiteness length, Bull. London Math. Soc. 44(6) (2012), 1209–1214. ISSN: 0024-6093. doi: 10.1112/blms/bds047.Google Scholar
Gromov, M., Asymptotic invariants of infinite groups, in Geometric group theory, Vol. 2 (Sussex, 1991), London Mathematical Society Lecture Note Series, vol. 182 (Cambridge University Press, Cambridge, 1993), 1–295.Google Scholar
Hughes, S., Equivariant cohomology, lattices, and trees, PhD Thesis (School of Mathematical Sciences, University of Southampton, 2021).Google Scholar
Hughes, S., Lattices in a product of trees, hierarchically hyperbolic groups, and virtual torsion-freeness, Bull. London Math. Soc. doi: 10.1112/blms.12637
CrossRefGoogle Scholar
Hughes, S., Irreducible lattices fibring over the circle (2022). arXiv:2201.06525 [math.GR].Google Scholar
Hughes, S. and Valiunas, M., Commensurating HNN-extensions: hierarchical hyperbolicity and biautomaticity (2021). arXiv: 2203.11996 [math.GR].Google Scholar
Lück, W.,
 $\textit{L}^{2}$
-invariants: theory and applications to geometry and K-theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas.
$\textit{L}^{2}$
-invariants: theory and applications to geometry and K-theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas.
 ${3}^{rd}$
Series. A Series of Modern Surveys in Mathematics], vol. 44 (Springer-Verlag, Berlin, 2002), xvi+595. iSBN: 3-540-43566-2. doi: 10.1007/978-3-662-04687-6.Google Scholar
${3}^{rd}$
Series. A Series of Modern Surveys in Mathematics], vol. 44 (Springer-Verlag, Berlin, 2002), xvi+595. iSBN: 3-540-43566-2. doi: 10.1007/978-3-662-04687-6.Google Scholar
Petersen, H. D., Sauer, R. and Thom, A.,
 $\textit{L}^{2}$
-Betti numbers of totally disconnected groups and their approximation by Betti numbers of lattices, J. Topol. 11(1) (2018), 257–282. ISSN: 1753–8416. doi: 10.1112/topo.12056.Google Scholar
$\textit{L}^{2}$
-Betti numbers of totally disconnected groups and their approximation by Betti numbers of lattices, J. Topol. 11(1) (2018), 257–282. ISSN: 1753–8416. doi: 10.1112/topo.12056.Google Scholar


