Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T06:46:22.078Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of irreducible tournaments

Published online by Cambridge University Press:  18 May 2009

E. M. Wright
E. M. Wright
Affiliation:
University of Aberdeen
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

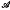An n-tournament is a set of n labelled points, each pair A, B of which is joined either by the oriented line AB or by the oriented line BA. There are N = n(n –1)/2 such pairs and so Fn different n-tournaments, where Fn = 2N. A tournament is reducible if the points can be separated into two non-empty subsets and ℬ, such that every line joining a point in 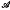to a point in ℬ is directed towards the point in ℬ. Rado [3] showed that an irreducible tournamentis strongly connected; i.e. for every ordered pair of points A, B, there is a sequence of correctly oriented lines AC1, C1C2, …, ChB in the tournament, and conversely that a strongly connected tournament is irreducible.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 11 , Issue 2 , July 1970 , pp. 97 - 101
Copyright
Copyright © Glasgow Mathematical Journal Trust 1970

References

REFERENCES

1.Moon, J. W. and Moser, L., Almost all tournaments are irreducible, Canadian Math. Bull. 5 (1962), 61–65.CrossRefGoogle Scholar
2.Moon, J. W., Topics on tournaments (New York, 1968).Google Scholar
3.Rado, R., Theorems on linear combinatorial topology and general measure, Ann. of Math. 44 (1943), 228–270.CrossRefGoogle Scholar