Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T21:34:36.707Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of sparsely edged labelled Hamiltonian graphs

Published online by Cambridge University Press:  18 May 2009

E. M. Wright
E. M. Wright
Affiliation:
University of Aberdeen, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An (n, q) graph is a graph on n labelled points and q lines, no loops and no multiple lines. We write N = ½n(n – 1), B(a, b) = a!/{b!(a – b)!} and B(a, 0) = 1, so that there are just B(N, q)different (n, q) graphs. Again h(n, q) is the number of Hamiltonian (n, q) graphs. Much attention has been devoted to the problem of determining for which q = q(n) “almost all” (n, q) graphs are Hamiltonian, i.e. for which q we have

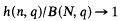
as n → ∞. I proved [8, Theorem 4] that qn–3/2; → ∞ is a sufficient condition by showing that, for such q, almost all (n, q) graphs have about the average number of Hamiltonian circuits (H.c.s).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 1 , January 1983 , pp. 83 - 87
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Cayley, A., A theorem on trees, Quart. J. Math. 23 (1889), 376–378.Google Scholar
2.Erdös, P. and Rényi, A., On the evolution of random graphs, Magyar Tud. Akad. Mat. Kutato Int. Kozl. 5 (1960), 17–61; reprinted in P. Erdös, The art of counting (M.I.T. Press, 1973), 574–617.Google Scholar
3.Erdös, P. and Rényi, A., On the strength of connectedness of a random graph, Ada Math. Acad. Set. Hungar. 12 (1961), 261–267; reprinted in P. Erdös, The art of counting (M.I.T. Press, 1973), 618–624.CrossRefGoogle Scholar
4.Gray, P. M. D., Murray, A. M. and Young, N. A., Wright's formulae for the number of connected sparsely edged graphs, J. Graph Theory 1 (1977), 331–334.CrossRefGoogle Scholar
5.Koršnov, A. D., Solution of a problem of Erdös and Rényi on Hamiltonian cycles in nonoriented graphs, Soviet Math. Dokl. 17 (1976), 760–764; (Dokl. Akad. Nauk SSSR 228 (1976), no. 3, 529–532).Google Scholar
6.Moon, J. W., Various proofs of Cayley's formula for counting trees, A seminar on graph theory, ed. Harary, F. (Holt, Rinehart and Winston, 1967), 70–78.Google Scholar
7.Rényi, A., On connected graphs I, Magyar Tud. Akad. Mat. Kutató Int. Közl. 4 (1959), 385–388.Google Scholar
8.Wright, E. M., For how many edges is a graph almost certainly Hamiltonian?, J. London Math. Soc. (2) 8 (1974), 44–48.CrossRefGoogle Scholar
9.Wright, E. M., The number of connected sparsely edged graphs, J. Graph Theory 1 (1977), 317–330.CrossRefGoogle Scholar
10.Wright, E. M., The number of connected sparsely edged graphs. II. Smooth graphs and blocks, J. Graph Theory 2 (1978), 299–305.CrossRefGoogle Scholar
11.Wright, E. M., The number of connected sparsely edged graphs. III. Asymptotic results, J. Graph Theory 4 (1980), 393–407.CrossRefGoogle Scholar