Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mihăilescu, Mihai
Moroşanu, Gheorghe
and
Stancu-Dumitru, Denisa
2011.
Equations involving a variable exponent Grushin-type operator.
Nonlinearity,
Vol. 24,
Issue. 10,
p.
2663.
Mihailescu, Mihai
and
Stancu-Dumitru, Denisa
2012.
ANISOTROPIC QUASILINEAR ELLIPTIC EQUATIONS WITH VARIABLE EXPONENT.
Journal of the Korean Mathematical Society,
Vol. 49,
Issue. 6,
p.
1123.
Stancu-Dumitru, Denisa
2012.
TWO NONTRIVIAL SOLUTIONS FOR A CLASS OF ANISOTROPIC VARIABLE EXPONENT PROBLEMS.
Taiwanese Journal of Mathematics,
Vol. 16,
Issue. 4,
Chung, Nguyen Thanh
and
Toan, Hoang Quoc
2014.
On a class of anisotropic elliptic equations without Ambrosetti–Rabinowitz type conditions.
Nonlinear Analysis: Real World Applications,
Vol. 16,
Issue. ,
p.
132.
Yu, Lujuan
and
Li, Fengquan
2018.
The Stability of Eigenvalues for the p(x)-Laplacian Equations Involving Robin Boundary Conditions.
Journal of Dynamical and Control Systems,
Vol. 24,
Issue. 2,
p.
223.
Taarabti, Said
El Allali, Zakaria
and
Haddouch, Khalil Ben
2019.
On an eigenvalue problem for an anisotropic elliptic equation.
Vol. 2074,
Issue. ,
p.
020024.
Kissi, Fouad
and
El Amrouss, Abdelrachid
2024.
Multiplicity of solutions for anisotropic Dirichlet problem with variable exponent.
Boletim da Sociedade Paranaense de Matemática,
Vol. 42,
Issue. ,
p.
1.
Figueiredo, Giovany Malcher
and
Razani, Abdolrahman
2024.
Infinitely many solutions for an anisotropic differential inclusion on unbounded domains.
Electronic Journal of Qualitative Theory of Differential Equations,
p.
1.
Razani, Abdolrahman
and
Tornatore, Elisabetta
2024.
Solutions for nonhomogeneous degenerate quasilinear anisotropic problems.
Constructive Mathematical Analysis,
Vol. 7,
Issue. 3,
p.
134.
Mahanta, Deepak Kumar
2025.
Existence and multiplicity of solutions for a class of quasilinear anisotropic elliptic systems via fibering method.
The Journal of Analysis,
Vol. 33,
Issue. 5,
p.
2117.
El Hachimi, Abderrahmane
and
Ouannasser, Anass
2025.
Parametric anisotropic elliptic problems with variable exponents and convection terms.
Journal of Elliptic and Parabolic Equations,
Vol. 11,
Issue. 1,
p.
135.

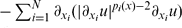 = λ|
= λ|