Article contents
On approximating Lebesgue integrals by Riemann sums
Published online by Cambridge University Press: 18 May 2009
Extract
If f is a real function, periodic with period 1, we define
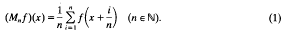
In the whole paper we write ∫ for 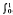 , mE for the Lebesgue measure of E ∩ [0,1], where E ⊂ ℝ is any measurable set of period 1, and we also use XE for the characteristic function of the set E. Consistent with this, the meaning of ℒp is ℒp [0, 1]. For all real xwe have
, mE for the Lebesgue measure of E ∩ [0,1], where E ⊂ ℝ is any measurable set of period 1, and we also use XE for the characteristic function of the set E. Consistent with this, the meaning of ℒp is ℒp [0, 1]. For all real xwe have

if f is Riemann-integrable on [0, 1]. However,∫ f exists for all f ∈ ℒ1 and one would wish to extend the validity of (2). As easy examples show, (cf. [3], [7]), (2) does not hold for f ∈ ℒp in general if p < 2. Moreover, Rudin [4] showed that (2) may fail for all x even for the characteristic function of an open set, and so, to get a reasonable extension, it is natural to weaken (2) to
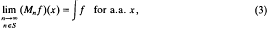
where S ⊂ ℕ is some “good” increasing subsequence of ℕ. Naturally, for different function classes ℱ ⊂ ℒ1 we get different meanings of being good. That is, we introduce the class of ℱ-good sequences as
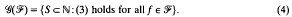
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1991
References
REFERENCES
- 1
- Cited by

