1. Introduction
The Arf invariant of a knot
![]() $K$
in
$K$
in
![]() $S^3$
is among the simplest and best understood knot invariants. It can be defined as follows. Let
$S^3$
is among the simplest and best understood knot invariants. It can be defined as follows. Let
![]() $F$
be a Seifert surface for
$F$
be a Seifert surface for
![]() $K$
, that is, an oriented connected compact surface smoothly embedded in
$K$
, that is, an oriented connected compact surface smoothly embedded in
![]() $S^3$
with oriented boundary
$S^3$
with oriented boundary
![]() $\partial F=K$
. Let
$\partial F=K$
. Let
![]() $q\colon H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
be the map given by
$q\colon H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
be the map given by
![]() $q(x)={\ell k}(x^-,x)$
, where
$q(x)={\ell k}(x^-,x)$
, where
![]() $\ell k$
stands for the linking number (here, reduced modulo 2), and
$\ell k$
stands for the linking number (here, reduced modulo 2), and
![]() $x^-\subset S^3\setminus F$
denotes the cycle
$x^-\subset S^3\setminus F$
denotes the cycle
![]() $x\subset F$
pushed in the negative normal direction off
$x\subset F$
pushed in the negative normal direction off
![]() $F$
. Then, the map
$F$
. Then, the map
![]() $q$
takes one of the two values in
$q$
takes one of the two values in
![]() $\mathbb{Z}_2$
more often than the other, and this value does not depend on the choice of the Seifert surface
$\mathbb{Z}_2$
more often than the other, and this value does not depend on the choice of the Seifert surface
![]() $F$
. It is therefore an invariant of the knot
$F$
. It is therefore an invariant of the knot
![]() $K$
, usually denoted by
$K$
, usually denoted by
![]() $\mathit{Arf}(K)\in \mathbb{Z}_2$
, and referred to as the Arf invariant (or Robertello invariant [Reference Robertello23]) of
$\mathit{Arf}(K)\in \mathbb{Z}_2$
, and referred to as the Arf invariant (or Robertello invariant [Reference Robertello23]) of
![]() $K$
. Extending it from knots to oriented links is straightforward as long as the link
$K$
. Extending it from knots to oriented links is straightforward as long as the link
![]() $L$
is such that
$L$
is such that
![]() ${\ell k}(K,L\setminus K)$
is even for each component
${\ell k}(K,L\setminus K)$
is even for each component
![]() $K$
of
$K$
of
![]() $L$
[Reference Robertello23]. Indeed, this condition ensures that
$L$
[Reference Robertello23]. Indeed, this condition ensures that
![]() $q$
induces a non-singular quadratic form, whose Arf invariant (in the sense of the original article of Arf [Reference Arf2]) can then be used, see Section 2.2 below.
$q$
induces a non-singular quadratic form, whose Arf invariant (in the sense of the original article of Arf [Reference Arf2]) can then be used, see Section 2.2 below.
The Arf invariant of knots enjoys a number of remarkable properties. First of all, it is an invariant of knot concordance [Reference Robertello23]; more precisely, a knot has vanishing Arf invariant if and only if it is 0-solvable in the sense of Cochran-Orr-Teichner [Reference Cochran, Orr and Teichner6]. Also, it can be retrieved from the Alexander polynomial of
![]() $K$
evaluated at
$K$
evaluated at
![]() $t=-1$
, as it coincides with the parity of the second coefficient of the Conway polynomial of
$t=-1$
, as it coincides with the parity of the second coefficient of the Conway polynomial of
![]() $K$
[Reference Levine19, Reference Murasugi22, Reference Robertello23]. Furthermore, it can be computed from the Jones polynomial evaluated at
$K$
[Reference Levine19, Reference Murasugi22, Reference Robertello23]. Furthermore, it can be computed from the Jones polynomial evaluated at
![]() $t=i$
, see for example [Reference Lickorish21, Chapter 10]. Finally, it admits a number of alternative interpretations, for example, in terms of the cobordism class of the 0-surgery of
$t=i$
, see for example [Reference Lickorish21, Chapter 10]. Finally, it admits a number of alternative interpretations, for example, in terms of the cobordism class of the 0-surgery of
![]() $K$
[Reference Cochran, Orr and Teichner6, Remark 8.2] (see also [Reference Conway and Nagel10, Section 5.2] for details), and in terms of twisted Whitney towers [Reference Conant, Schneiderman and Teichner7, Lemma 10] (see also [Reference Feller, Miller, Nagel, Orson, Powell and Ray14, Proposition 6.4]).
$K$
[Reference Cochran, Orr and Teichner6, Remark 8.2] (see also [Reference Conway and Nagel10, Section 5.2] for details), and in terms of twisted Whitney towers [Reference Conant, Schneiderman and Teichner7, Lemma 10] (see also [Reference Feller, Miller, Nagel, Orson, Powell and Ray14, Proposition 6.4]).
As mentioned above, the Arf invariant of an oriented link can be defined and computed using the Seifert form [Reference Seifert24], one of the most ubiquitous objects in classical knot theory. Other examples of invariants which can be defined, studied and computed using this tool include the Alexander-Conway polynomial [Reference Alexander1, Reference Conway11, Reference Kauffman17], the Alexander module [Reference Levine19, Reference Seifert24], the Levine-Tristram signature [Reference Levine20, Reference Tristram25, Reference Trotter26], and the Blanchfield form [Reference Blanchfield3, Reference Friedl and Powell15, Reference Kearton18].
These four invariants can be naturally extended from oriented links to so-called colored links, whose definition we now recall. An
![]() $m$
-colored link is an oriented link
$m$
-colored link is an oriented link
![]() $L$
each of whose components is endowed with a color in
$L$
each of whose components is endowed with a color in
![]() $\{1,\ldots ,m\}$
so that all colors are used. Such a colored link is commonly denoted by
$\{1,\ldots ,m\}$
so that all colors are used. Such a colored link is commonly denoted by
![]() $L=L_1\cup \ldots \cup L_m$
, with
$L=L_1\cup \ldots \cup L_m$
, with
![]() $L_i$
the sublink of
$L_i$
the sublink of
![]() $L$
consisting of the components of color
$L$
consisting of the components of color
![]() $i$
. Obviously, a
$i$
. Obviously, a
![]() $1$
-colored link is nothing but an oriented link, while an
$1$
-colored link is nothing but an oriented link, while an
![]() $m$
-component
$m$
-component
![]() $m$
-colored link is an oriented ordered link.
$m$
-colored link is an oriented ordered link.
Let us now be more precise about the aforementioned extensions: for
![]() $m$
-colored links, one can define
$m$
-colored links, one can define
![]() $m$
-variable versions of the Alexander-Conway polynomial [Reference Conway11, Reference Hartley16], of the Alexander module [Reference Alexander1], of the Levine-Tristram signature [Reference Cimasoni and Florens5], and of the Blanchfield form [Reference Blanchfield3]. Moreover, each of these invariants can be defined and studied using generalized Seifert surfaces known as C-complexes, first introduced by Cooper [Reference Cooper12] for 2-component links and extended to general colored links in [Reference Cimasoni4], see Sections 2.3 and 2.4 below. We refer the interested reader to [Reference Cimasoni4] for such a geometric construction of the Alexander-Conway multivariable polynomial, to [Reference Cimasoni and Florens5] for the Alexander module and Levine-Tristram signature, and to [Reference Conway8, Reference Conway, Friedl and Toffoli9] for the Blanchfield pairing.
$m$
-variable versions of the Alexander-Conway polynomial [Reference Conway11, Reference Hartley16], of the Alexander module [Reference Alexander1], of the Levine-Tristram signature [Reference Cimasoni and Florens5], and of the Blanchfield form [Reference Blanchfield3]. Moreover, each of these invariants can be defined and studied using generalized Seifert surfaces known as C-complexes, first introduced by Cooper [Reference Cooper12] for 2-component links and extended to general colored links in [Reference Cimasoni4], see Sections 2.3 and 2.4 below. We refer the interested reader to [Reference Cimasoni4] for such a geometric construction of the Alexander-Conway multivariable polynomial, to [Reference Cimasoni and Florens5] for the Alexander module and Levine-Tristram signature, and to [Reference Conway8, Reference Conway, Friedl and Toffoli9] for the Blanchfield pairing.
This work is an attempt to construct generalized Arf invariants of colored links using similar techniques. On the one hand, this attempt is rather successful, as testified by our main result (see Section 3.1 for the construction, Theorem3.1 for a more complete version, together with Remarks 3.2 and 3.3 showing that all the hypotheses are necessary).
Theorem 1.1. Let
![]() $L$
be an
$L$
be an
![]() $m$
-colored link, and let
$m$
-colored link, and let
![]() $F$
be a C-complex for
$F$
be a C-complex for
![]() $L$
. For each
$L$
. For each
![]() $E\subset \{\pm \}^m$
of even cardinality, there is a quadratic form
$E\subset \{\pm \}^m$
of even cardinality, there is a quadratic form
![]() $q_F^E\colon H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
such that one of the following statements holds, the same one for any choice of
$q_F^E\colon H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
such that one of the following statements holds, the same one for any choice of
![]() $F$
:
$F$
:
-
(i)
 $q_F^E$
induces a non-singular quadratic form, with Arf invariant
$q_F^E$
induces a non-singular quadratic form, with Arf invariant
 $0$
;
$0$
; -
(ii)
 $q_F^E$
induces a non-singular quadratic form, with Arf invariant
$q_F^E$
induces a non-singular quadratic form, with Arf invariant
 $1$
;
$1$
; -
(iii)
 $q_F^E$
does not induce a non-singular quadratic form.
$q_F^E$
does not induce a non-singular quadratic form.
As will be made clear in Section 3.1, the classical Arf invariant corresponds to the case
![]() $m=1$
and the choice of a sign, that is of an odd subset
$m=1$
and the choice of a sign, that is of an odd subset
![]() $E\subset \{\pm \}$
. However, for
$E\subset \{\pm \}$
. However, for
![]() $m\gt 1$
, only even subsets
$m\gt 1$
, only even subsets
![]() $E\subset \{\pm \}^m$
yield invariants (see Remark 3.2). By Theorem1.1, any such
$E\subset \{\pm \}^m$
yield invariants (see Remark 3.2). By Theorem1.1, any such
![]() $E\subset \{\pm \}^m$
of even cardinality defines an Arf invariant for some class of
$E\subset \{\pm \}^m$
of even cardinality defines an Arf invariant for some class of
![]() $m$
-colored links which depends on
$m$
-colored links which depends on
![]() $E$
.
$E$
.
On the other hand, our attempt can be considered as unsuccessful, due to the following fact.
Proposition 1.2. For any
![]() $m$
-colored link
$m$
-colored link
![]() $L$
and any
$L$
and any
![]() $E\subset \{\pm \}^m$
of even cardinality, the trichotomy of Theorem 1.1 is determined by the linking numbers of the components of
$E\subset \{\pm \}^m$
of even cardinality, the trichotomy of Theorem 1.1 is determined by the linking numbers of the components of
![]() $L$
.
$L$
.
In conclusion, this note should serve as a cautionary tale for anyone interested in extending the Arf invariant in this manner.
This paper is organized as follows. In Section 2, we recall the necessary background: the Arf invariant of a quadratic form, the Arf invariant of a link, C-complexes and generalized Seifert matrices are dealt with in individual paragraphs. Section 3 contains the proof of Theorem1.1, and Section 4 the proof of Proposition 1.2. Finally, Appendix A deals with generalized S-equivalence.
2. Background on Arf invariants and generalized Seifert forms
This section contains all the background needed for this work: we review the Arf invariant of a quadratic form in Section 2.1, the Arf invariant of an oriented link in Section 2.2, C-complexes in Section 2.3, and the associated generalized Seifert matrices in Section 2.4.
2.1. The Arf invariant of a quadratic form
In this section and the following one, we briefly recall the definition of the Arf invariant of a quadratic form [Reference Arf2] and of an oriented link [Reference Robertello23], following [Reference Lickorish21, Chapter 10] and referring to it for proofs and details.
Let
![]() $V$
be a finite-dimensional
$V$
be a finite-dimensional
![]() $\mathbb{Z}_2$
-vector space. A function
$\mathbb{Z}_2$
-vector space. A function
![]() $q\colon V\to \mathbb{Z}_2$
is a quadratic form if there exists a bilinear map
$q\colon V\to \mathbb{Z}_2$
is a quadratic form if there exists a bilinear map
![]() $B\colon V\times V \to \mathbb{Z}_2$
such that
$B\colon V\times V \to \mathbb{Z}_2$
such that
![]() $q(x+y)+q(x)+q(y)=B(x,y)$
for all
$q(x+y)+q(x)+q(y)=B(x,y)$
for all
![]() $x,y\in V$
. The quadratic form
$x,y\in V$
. The quadratic form
![]() $q$
is called non-singular if the bilinear map
$q$
is called non-singular if the bilinear map
![]() $B$
itself is non-singular, that is if its radical
$B$
itself is non-singular, that is if its radical
is trivial. In this case, since the non-singular bilinear map
![]() $B$
also satisfies
$B$
also satisfies
![]() $B(x,x)=0$
for all
$B(x,x)=0$
for all
![]() $x\in V$
, it is by definition a symplectic form. Such forms are known to exist only if
$x\in V$
, it is by definition a symplectic form. Such forms are known to exist only if
![]() $V$
has even dimension, say
$V$
has even dimension, say
![]() $2n$
. It can then be shown that, as
$2n$
. It can then be shown that, as
![]() $x$
varies over the
$x$
varies over the
![]() $2^{2n}$
elements of
$2^{2n}$
elements of
![]() $V$
,
$V$
,
![]() $q(x)$
takes one of the values,
$q(x)$
takes one of the values,
![]() $0$
or
$0$
or
![]() $1$
, more often (namely
$1$
, more often (namely
![]() $2^{2n-1}+2^{n-1}$
times), than the other one (
$2^{2n-1}+2^{n-1}$
times), than the other one (
![]() $2^{2n-1}-2^{n-1}$
times). This leads to what is sometimes referred to as the “democratic invariant” of
$2^{2n-1}-2^{n-1}$
times). This leads to what is sometimes referred to as the “democratic invariant” of
![]() $q$
.
$q$
.
Definition 2.1. The Arf invariant
![]() $\mathit{Arf}(q)\in \mathbb{Z}_2$
of a non-singular quadratic form
$\mathit{Arf}(q)\in \mathbb{Z}_2$
of a non-singular quadratic form
![]() $q$
is the value taken the most often by
$q$
is the value taken the most often by
![]() $q(x)$
as
$q(x)$
as
![]() $x$
varies over the elements of
$x$
varies over the elements of
![]() $V$
.
$V$
.
A closed formula defining the Arf invariant is easily seen to be given by
A more practical formula, due to Cahit Arf,Footnote
1
uses a symplectic basis of
![]() $V$
, i.e. a basis
$V$
, i.e. a basis
![]() $e_1,f_1,\ldots ,e_n,f_n$
such that
$e_1,f_1,\ldots ,e_n,f_n$
such that
![]() $B(e_i,e_j)=B(f_i,f_j)=0$
and
$B(e_i,e_j)=B(f_i,f_j)=0$
and
![]() $B(e_i,f_j)=\delta _{ij}$
for all
$B(e_i,f_j)=\delta _{ij}$
for all
![]() $1\le i,j\le n$
. It reads:
$1\le i,j\le n$
. It reads:
One of the main results of Arf in [Reference Arf2] is that two non-singular quadratic forms are isomorphic if and only if they have same dimension and same Arf invariant.
This invariant can be extended to a possibly singular quadratic form
![]() $q\colon V\to \mathbb{Z}_2$
as long as it vanishes on the radical of the associated bilinear form
$q\colon V\to \mathbb{Z}_2$
as long as it vanishes on the radical of the associated bilinear form
![]() $B$
. In such a case indeed, the map
$B$
. In such a case indeed, the map
![]() $q\colon V\to \mathbb{Z}_2$
induces a well-defined non-singular quadratic form
$q\colon V\to \mathbb{Z}_2$
induces a well-defined non-singular quadratic form
![]() $\overline {q}\colon V/\operatorname {rad}(B)\to \mathbb{Z}_2$
, whose Arf invariant can be considered. On the other hand, if
$\overline {q}\colon V/\operatorname {rad}(B)\to \mathbb{Z}_2$
, whose Arf invariant can be considered. On the other hand, if
![]() $q$
does not vanish on
$q$
does not vanish on
![]() $\operatorname {rad}(B)$
, then its Arf invariant is not defined.Footnote
2
$\operatorname {rad}(B)$
, then its Arf invariant is not defined.Footnote
2
In summary, an arbitrary quadratic form
![]() $q\colon V\to \mathbb{Z}_2$
always satisfies the following trichotomy: either it induces a non-singular quadratic form with Arf invariant
$q\colon V\to \mathbb{Z}_2$
always satisfies the following trichotomy: either it induces a non-singular quadratic form with Arf invariant
![]() $0$
, or it induces a non-singular quadratic form with Arf invariant
$0$
, or it induces a non-singular quadratic form with Arf invariant
![]() $1$
, or it does not induce a non-singular quadratic form. We shall simply denote these three possibilities by
$1$
, or it does not induce a non-singular quadratic form. We shall simply denote these three possibilities by
![]() $\mathit{Arf}(q)=0$
,
$\mathit{Arf}(q)=0$
,
![]() $\mathit{Arf}(q)=1$
, and
$\mathit{Arf}(q)=1$
, and
![]() $\mathit{Arf}(q)$
undefined, and call these three cases the three possible values for
$\mathit{Arf}(q)$
undefined, and call these three cases the three possible values for
![]() $\mathit{Arf}(q)$
.
$\mathit{Arf}(q)$
.
2.2. The Arf invariant of an oriented link
As already mentioned in the introduction, this theory can be applied to knots and links, in the following way. Let
![]() $L$
be an oriented link in
$L$
be an oriented link in
![]() $S^3$
, and let
$S^3$
, and let
![]() $F$
be a Seifert surface for
$F$
be a Seifert surface for
![]() $L$
. Let
$L$
. Let
![]() $q\colon H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
be the associated Seifert form reduced modulo 2 and restricted to the diagonal. In other words, the map
$q\colon H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
be the associated Seifert form reduced modulo 2 and restricted to the diagonal. In other words, the map
![]() $q$
is defined by
$q$
is defined by
![]() $q(x)={\ell k}(x^-,x)$
, where
$q(x)={\ell k}(x^-,x)$
, where
![]() $\ell k$
stands for the linking number reduced modulo 2 and
$\ell k$
stands for the linking number reduced modulo 2 and
![]() $x^-\subset S^3\setminus F$
denotes the cycle
$x^-\subset S^3\setminus F$
denotes the cycle
![]() $x\subset F$
pushed in the negative direction off the oriented surface
$x\subset F$
pushed in the negative direction off the oriented surface
![]() $F$
. For any
$F$
. For any
![]() $x,y\in H_1(F;\,\mathbb{Z}_2)$
, we have
$x,y\in H_1(F;\,\mathbb{Z}_2)$
, we have
with
![]() $B\colon H_1(F;\,\mathbb{Z}_2)\times H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
the modulo 2 intersection form. Therefore, we see that the map
$B\colon H_1(F;\,\mathbb{Z}_2)\times H_1(F;\,\mathbb{Z}_2)\to \mathbb{Z}_2$
the modulo 2 intersection form. Therefore, we see that the map
![]() $q$
is a quadratic form.
$q$
is a quadratic form.
This form is singular unless
![]() $L$
is a knot, as
$L$
is a knot, as
![]() $\operatorname {rad}(B)$
is generated by the cycles given by the boundary components of
$\operatorname {rad}(B)$
is generated by the cycles given by the boundary components of
![]() $F$
, that is, the components of
$F$
, that is, the components of
![]() $L$
. For
$L$
. For
![]() $q$
to induce a non-singular quadratic form
$q$
to induce a non-singular quadratic form
![]() $\overline {q}$
on the quotient
$\overline {q}$
on the quotient
![]() $H_1(F;\,\mathbb{Z}_2)/\operatorname {rad}(B)$
, we therefore need
$H_1(F;\,\mathbb{Z}_2)/\operatorname {rad}(B)$
, we therefore need
![]() $q$
to vanish on the components of
$q$
to vanish on the components of
![]() $L$
. This is the case if and only if
$L$
. This is the case if and only if
![]() ${\ell k}(K,L\setminus K)$
is even for each component
${\ell k}(K,L\setminus K)$
is even for each component
![]() $K$
of
$K$
of
![]() $L$
.
$L$
.
Definition 2.2. Let
![]() $L$
be an oriented link with
$L$
be an oriented link with
![]() ${\ell k}(K,L\setminus K)$
even for each component
${\ell k}(K,L\setminus K)$
even for each component
![]() $K\subset L$
. The Arf invariant
$K\subset L$
. The Arf invariant
![]() $\mathit{Arf}(L)\in \mathbb{Z}_2$
of
$\mathit{Arf}(L)\in \mathbb{Z}_2$
of
![]() $L$
is the Arf invariant of the induced non-singular quadratic form
$L$
is the Arf invariant of the induced non-singular quadratic form
![]() $\overline {q}$
.
$\overline {q}$
.
To prove that this is a well-defined invariant, one needs to check that it does not depend on the choice of the Seifert surface
![]() $F$
for
$F$
for
![]() $L$
. By a classical result (see e.g. [Reference Lickorish21, Chapter 8]), two Seifert surfaces for the same link are connected by a finite sequence of ambient isotopies and handle attachments. This translates into an equivalence relation on Seifert matrices, known as S-equivalence, and it is an easy exercise to check that S-equivalent matrices yield the same Arf invariant.
$L$
. By a classical result (see e.g. [Reference Lickorish21, Chapter 8]), two Seifert surfaces for the same link are connected by a finite sequence of ambient isotopies and handle attachments. This translates into an equivalence relation on Seifert matrices, known as S-equivalence, and it is an easy exercise to check that S-equivalent matrices yield the same Arf invariant.
2.3. C-complexes for colored links
The goal of this section is to introduce generalized Seifert surfaces for colored links. We start by recalling the definition of a colored link already sketched in the introduction.
Definition 2.3. Let
![]() $m$
be a positive integer. An
$m$
be a positive integer. An
![]() $m$
-colored link is an oriented link
$m$
-colored link is an oriented link
![]() $L$
in
$L$
in
![]() $S^3$
together with a surjective map assigning to each component of
$S^3$
together with a surjective map assigning to each component of
![]() $L$
a color in
$L$
a color in
![]() $\{1,\ldots ,m\}$
. Two colored links
$\{1,\ldots ,m\}$
. Two colored links
![]() $L$
and
$L$
and
![]() $L'$
are said to be isotopic if there exists an isotopy between
$L'$
are said to be isotopic if there exists an isotopy between
![]() $L$
and
$L$
and
![]() $L'$
preserving the orientation and color of each component.
$L'$
preserving the orientation and color of each component.
We denote a colored link by
![]() $L=L_1\cup \ldots \cup L_m$
, where
$L=L_1\cup \ldots \cup L_m$
, where
![]() $L_i$
stands for the sublink of
$L_i$
stands for the sublink of
![]() $L$
made of the components of color
$L$
made of the components of color
![]() $i$
. Colored links should be thought of as natural generalizations of oriented links, which correspond to the case
$i$
. Colored links should be thought of as natural generalizations of oriented links, which correspond to the case
![]() $m=1$
.
$m=1$
.

Figure 1. Left: a clasp intersection. Right: a well-behaved cycle crossing such a clasp intersection.
The corresponding generalized notion of Seifert surface is due to Cooper [Reference Cooper12], who defined it for 2-component 2-colored links, objects which were subsequently extended to arbitrary colored links in [Reference Cimasoni4].
Definition 2.4. A C-complex for an
![]() $m$
-colored link
$m$
-colored link
![]() $L=L_1\cup \ldots \cup L_m$
is a union
$L=L_1\cup \ldots \cup L_m$
is a union
![]() $F=F_1\cup \ldots \cup F_m$
of surfaces embedded in
$F=F_1\cup \ldots \cup F_m$
of surfaces embedded in
![]() $S^3$
such that
$S^3$
such that
![]() $F$
is connected and satisfies the following conditions:
$F$
is connected and satisfies the following conditions:
-
(1) for all
 $i$
, the surface
$i$
, the surface
 $F_i$
is a Seifert surface for
$F_i$
is a Seifert surface for
 $L_i$
;
$L_i$
; -
(2) for all
 $i\neq j$
, the surfaces
$i\neq j$
, the surfaces
 $F_i$
and
$F_i$
and
 $F_j$
are either disjoint or intersect in a finite number of clasps (see Figure 1);
$F_j$
are either disjoint or intersect in a finite number of clasps (see Figure 1); -
(3) for all
 $i,j,k$
pairwise distinct, the intersection
$i,j,k$
pairwise distinct, the intersection
 $F_i\cap F_j\cap F_k$
is empty.
$F_i\cap F_j\cap F_k$
is empty.
Such a C-complex is said to be totally connected if
![]() $F_i\cap F_j$
is nonempty for all
$F_i\cap F_j$
is nonempty for all
![]() $i\neq j$
.
$i\neq j$
.
The existence of a (totally connected) C-complex for any given colored link is fairly easy to establish, see [Reference Cimasoni4]. On the other hand, relating two C-complexes for isotopic colored links is more difficult [Reference Cimasoni4, Reference Cimasoni and Florens5], and the correct version appeared only recently, see Theorem 1.3 of [Reference Davis, Martin and Otto13].
In the context of our work, we need to know how two totally connected C-complexes for isotopic colored links are related. In fact, Theorem 1.3 of [Reference Davis, Martin and Otto13] pertains to a more general version of C-complexes: they are not necessarily totally connected, and the surfaces
![]() $F_i$
are not assumed to be connected. Fortunately, the results of [Reference Davis, Martin and Otto13] do imply the following lemma. In order not to break the flow of the reading, we differ its proof to Appendix A.
$F_i$
are not assumed to be connected. Fortunately, the results of [Reference Davis, Martin and Otto13] do imply the following lemma. In order not to break the flow of the reading, we differ its proof to Appendix A.
Lemma 2.5 ([Reference Davis, Martin and Otto13]). Let
![]() $F$
and
$F$
and
![]() $F'$
be two totally connected C-complexes for isotopic colored links. Then, there exist totally connected C-complexes
$F'$
be two totally connected C-complexes for isotopic colored links. Then, there exist totally connected C-complexes
![]() $F=F^1,F^2,\ldots ,F^{n-1},F^n=F'$
such that for all
$F=F^1,F^2,\ldots ,F^{n-1},F^n=F'$
such that for all
![]() $1\le k \lt n$
,
$1\le k \lt n$
,
![]() $F^{k+1}$
is obtained from
$F^{k+1}$
is obtained from
![]() $F^k$
by one of the following moves or its inverse:
$F^k$
by one of the following moves or its inverse:
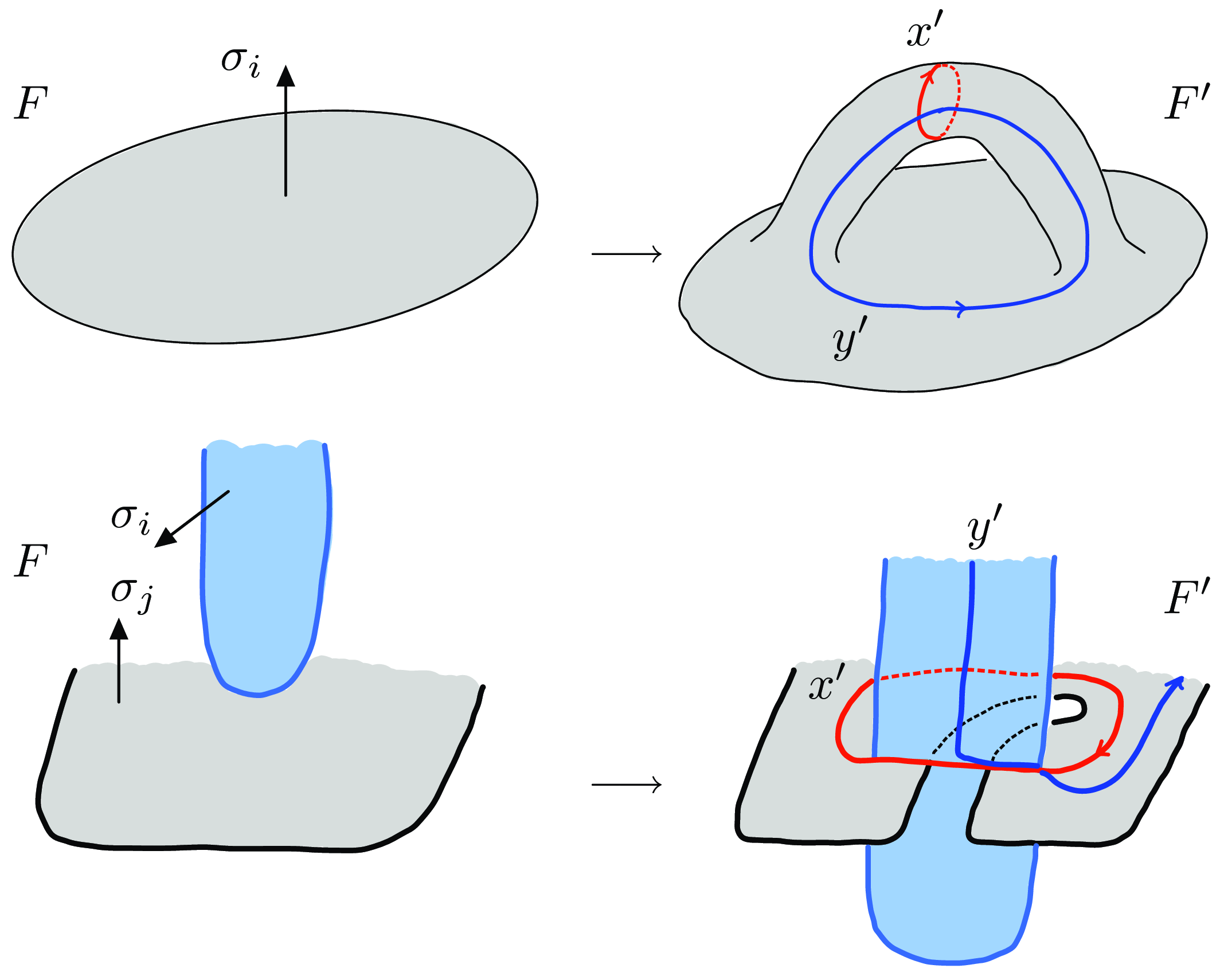
Figure 2. For the moves (T1) and (T2), a basis of
![]() $H_1(F')$
is obtained by adding the cycles
$H_1(F')$
is obtained by adding the cycles
![]() $x'$
and
$x'$
and
![]() $y'$
to a basis of
$y'$
to a basis of
![]() $H_1(F)$
.
$H_1(F)$
.
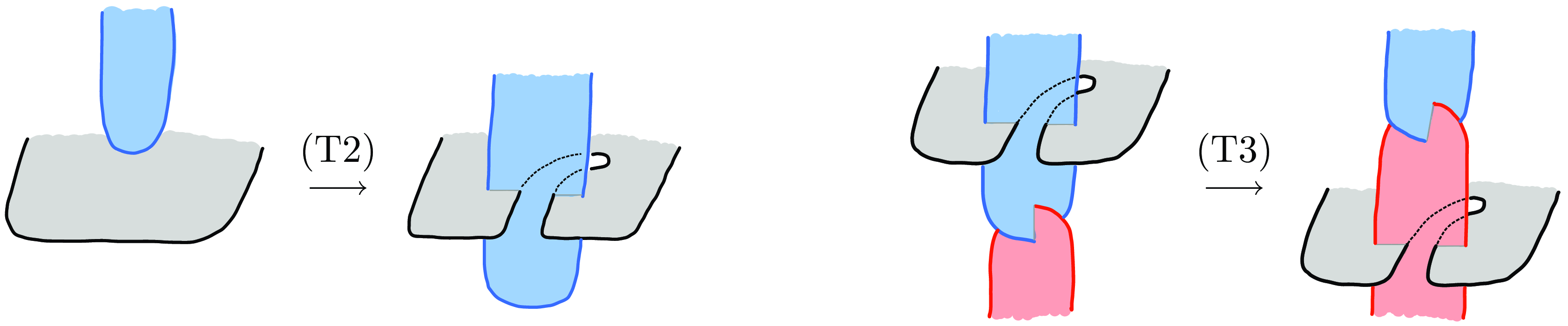
Figure 3. The movements (T2) and (T3).
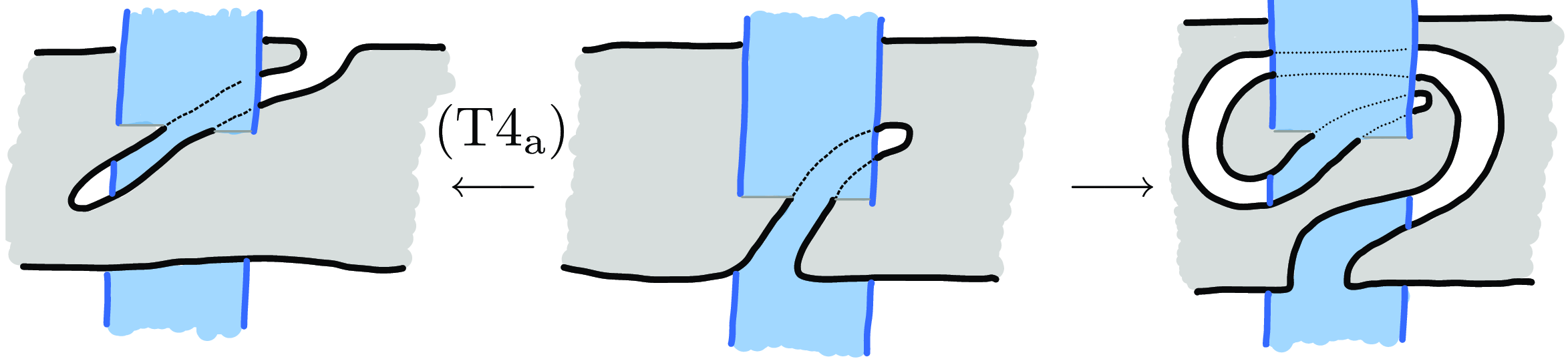
Figure 4. Examples of (T4) movements.
2.4. Generalized Seifert matrices
C-complexes allow to define generalized Seifert forms as follows. For any sign
![]() $\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _m)\in \{\pm \}^m$
, let
$\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _m)\in \{\pm \}^m$
, let
be the bilinear form given by
![]() $\alpha ^\varepsilon (x,y)={\ell k}(x^\varepsilon ,y)$
, where
$\alpha ^\varepsilon (x,y)={\ell k}(x^\varepsilon ,y)$
, where
![]() $x^\varepsilon \subset S^3\setminus F$
denotes a cycle representating the homology class
$x^\varepsilon \subset S^3\setminus F$
denotes a cycle representating the homology class
![]() $x\in H_1(F)$
pushed in the
$x\in H_1(F)$
pushed in the
![]() $\varepsilon _i$
-normal direction off
$\varepsilon _i$
-normal direction off
![]() $F_i$
for all
$F_i$
for all
![]() $i=1,\ldots ,m$
. For this to make sense, one needs this cycle to be well-behaved when crossing clasps, as illustrated in the right-hand part of Figure 1. This is not an issue, as any homology class in
$i=1,\ldots ,m$
. For this to make sense, one needs this cycle to be well-behaved when crossing clasps, as illustrated in the right-hand part of Figure 1. This is not an issue, as any homology class in
![]() $H_1(F)$
can be represented by such well-behaved cycles. We denote by
$H_1(F)$
can be represented by such well-behaved cycles. We denote by
![]() $A^\varepsilon =A_F^\varepsilon$
the corresponding generalized Seifert matrices, defined with respect to a fix basis of
$A^\varepsilon =A_F^\varepsilon$
the corresponding generalized Seifert matrices, defined with respect to a fix basis of
![]() $H_1(F)$
. Note the equality
$H_1(F)$
. Note the equality
![]() $A^{-\varepsilon }=(A^\varepsilon )^{{\operatorname {T}}}$
for all
$A^{-\varepsilon }=(A^\varepsilon )^{{\operatorname {T}}}$
for all
![]() $\varepsilon \in \{\pm \}^m$
.
$\varepsilon \in \{\pm \}^m$
.
Note that in the case
![]() $m=1$
, a C-complex for a 1-colored link
$m=1$
, a C-complex for a 1-colored link
![]() $L$
is nothing but a Seifert surface for the oriented link
$L$
is nothing but a Seifert surface for the oriented link
![]() $L$
, a matrix
$L$
, a matrix
![]() $A^-$
corresponding to
$A^-$
corresponding to
![]() $\varepsilon =-$
is a standard Seifert matrix, and
$\varepsilon =-$
is a standard Seifert matrix, and
![]() $A^+$
its transpose.
$A^+$
its transpose.
As recalled in Section 2.2, two Seifert matrices for isotopic oriented links are related by a sequence of moves generating an equivalence relation known as S-equivalence. Since two totally connected C-complexes
![]() $F,F'$
for isotopic colored links
$F,F'$
for isotopic colored links
![]() $L,L'$
are related by the sequence of moves of Lemma 2.5, the corresponding generalized Seifert matrices
$L,L'$
are related by the sequence of moves of Lemma 2.5, the corresponding generalized Seifert matrices
![]() $A^\varepsilon _{F},A^\varepsilon _{F'}$
are related by a sequence of transformations (which in general depend on
$A^\varepsilon _{F},A^\varepsilon _{F'}$
are related by a sequence of transformations (which in general depend on
![]() $\varepsilon$
). Such computations were performed in [Reference Cimasoni4, Reference Davis, Martin and Otto13] for general C-complexes, but we need to consider the restrictive case of totally connected ones, yielding slightly different results.
$\varepsilon$
). Such computations were performed in [Reference Cimasoni4, Reference Davis, Martin and Otto13] for general C-complexes, but we need to consider the restrictive case of totally connected ones, yielding slightly different results.
Once again, in order not to include technical statements in this background section, we differ these computations to Appendix A.
3. Arf invariants of colored links
The goal of this section is to explain how the classical Arf invariant defined in Section 2.2 can be extended to colored links, that is to prove Theorem1.1. More precisely, we start in Section 3.1 with a discussion leading to the detailed statement of our main result. Its proof is given in Section 3.2 where we check independence of the C-complex.
3.1. Main result
From now on, we work over the field
![]() $\mathbb{Z}_2$
of modulo 2 integers, that will often be omitted from the notation. For example, given a C-complex
$\mathbb{Z}_2$
of modulo 2 integers, that will often be omitted from the notation. For example, given a C-complex
![]() $F$
for an
$F$
for an
![]() $m$
-colored link
$m$
-colored link
![]() $L$
and a sign
$L$
and a sign
![]() $\varepsilon \in \{\pm \}^m$
, we still denote by
$\varepsilon \in \{\pm \}^m$
, we still denote by
![]() $\alpha ^\varepsilon =\alpha _F^\varepsilon$
the form on
$\alpha ^\varepsilon =\alpha _F^\varepsilon$
the form on
![]() $H_1(F;\,\mathbb{Z}_2)$
given by the modulo 2 reduction of the generalized Seifert form, and by
$H_1(F;\,\mathbb{Z}_2)$
given by the modulo 2 reduction of the generalized Seifert form, and by
![]() $A^\varepsilon =A_F^\varepsilon$
the modulo 2 reduction of a corresponding generalized Seifert matrix.
$A^\varepsilon =A_F^\varepsilon$
the modulo 2 reduction of a corresponding generalized Seifert matrix.
To define a (generalized) Arf invariant of
![]() $L$
, we need a quadratic form. For any
$L$
, we need a quadratic form. For any
![]() $\varepsilon \in \{\pm \}^m$
, let us denote by
$\varepsilon \in \{\pm \}^m$
, let us denote by
![]() $q_F^\varepsilon$
(or by
$q_F^\varepsilon$
(or by
![]() $q^\varepsilon$
when no confusion is possible) the map
$q^\varepsilon$
when no confusion is possible) the map
defined by
![]() $q_F^\varepsilon (x)=\alpha ^\varepsilon _F(x,x)={\ell k}(x^\varepsilon ,x)$
. As in the classical case, we have
$q_F^\varepsilon (x)=\alpha ^\varepsilon _F(x,x)={\ell k}(x^\varepsilon ,x)$
. As in the classical case, we have
for any
![]() $x,y\in H_1(F;\,\mathbb{Z}_2)$
. Since
$x,y\in H_1(F;\,\mathbb{Z}_2)$
. Since
![]() $B_F^\varepsilon$
a bilinear form (with matrix
$B_F^\varepsilon$
a bilinear form (with matrix
![]() $A_F^\varepsilon +(A_F^\varepsilon )^{{\operatorname {T}}}$
), we see that the map
$A_F^\varepsilon +(A_F^\varepsilon )^{{\operatorname {T}}}$
), we see that the map
![]() $q_F^\varepsilon$
is a quadratic form. More generally, given any subset
$q_F^\varepsilon$
is a quadratic form. More generally, given any subset
![]() $E$
of
$E$
of
![]() $\{\pm \}^m$
, the map
$\{\pm \}^m$
, the map
is a quadratic form, with bilinear form
![]() $B_F^E\,:\!=\,\sum _{\varepsilon \in E}B_F^\varepsilon$
admitting the matrix
$B_F^E\,:\!=\,\sum _{\varepsilon \in E}B_F^\varepsilon$
admitting the matrix
![]() $A_F^E+(A_F^E)^{{\operatorname {T}}}$
, with
$A_F^E+(A_F^E)^{{\operatorname {T}}}$
, with
![]() $A_F^E\,:\!=\,\sum _{\varepsilon \in E}{A_F^\varepsilon }$
.
$A_F^E\,:\!=\,\sum _{\varepsilon \in E}{A_F^\varepsilon }$
.
As explained in Section 2.1, there are now three possibilities for the quadratic form
![]() $q_F^E$
: it might vanish on
$q_F^E$
: it might vanish on
![]() $\operatorname {rad}(B_F^E)$
, yielding the possible values
$\operatorname {rad}(B_F^E)$
, yielding the possible values
![]() $\mathit{Arf}(q_F^E)=0$
and
$\mathit{Arf}(q_F^E)=0$
and
![]() $\mathit{Arf}(q_F^E)=1$
; or it might not vanish on
$\mathit{Arf}(q_F^E)=1$
; or it might not vanish on
![]() $\operatorname {rad}(B_F^E)$
, yielding the third “value,” namely
$\operatorname {rad}(B_F^E)$
, yielding the third “value,” namely
![]() $\mathit{Arf}(q_F^E)$
undefined. This may or may not yield an invariant of
$\mathit{Arf}(q_F^E)$
undefined. This may or may not yield an invariant of
![]() $L$
, that is be independent of the choice of
$L$
, that is be independent of the choice of
![]() $F$
. If this is the case, then one can set
$F$
. If this is the case, then one can set
which might take the three values
![]() $0,1$
or undefined.
$0,1$
or undefined.
For example, the empty set
![]() $E=\emptyset$
yields the trivial (non-singular) quadratic form on the trivial space, leading to a well-defined, yet identically zero invariant. On the other hand, for
$E=\emptyset$
yields the trivial (non-singular) quadratic form on the trivial space, leading to a well-defined, yet identically zero invariant. On the other hand, for
![]() $m=1$
, both choices
$m=1$
, both choices
![]() $E=\{+\}$
and
$E=\{+\}$
and
![]() $E=\{-\}$
lead to the classical Arf invariant
$E=\{-\}$
lead to the classical Arf invariant
![]() $\mathit{Arf}_{\!E}(L)=\mathit{Arf}(L)$
, undefined unless
$\mathit{Arf}_{\!E}(L)=\mathit{Arf}(L)$
, undefined unless
![]() ${\ell k}(K,L\setminus K)$
is even for each component
${\ell k}(K,L\setminus K)$
is even for each component
![]() $K$
of
$K$
of
![]() $L$
, as explained in Section 2.2.
$L$
, as explained in Section 2.2.
The remaining cases are covered by the following reformulation of Theorem1.1 together with the ensuing remark.
Theorem 3.1. Let
![]() $L$
be an
$L$
be an
![]() $m$
-colored link. Given a totally connected C-complex
$m$
-colored link. Given a totally connected C-complex
![]() $F$
and a subset
$F$
and a subset
![]() $E$
of
$E$
of
![]() $\{\pm \}^m$
, let
$\{\pm \}^m$
, let
![]() $q_F^E\colon H_1(F;\,\,\mathbb{Z}_2)\to \mathbb{Z}_2$
be the associated quadratic form. If
$q_F^E\colon H_1(F;\,\,\mathbb{Z}_2)\to \mathbb{Z}_2$
be the associated quadratic form. If
![]() $E$
is of even cardinality, then the value of
$E$
is of even cardinality, then the value of
![]() $\mathit{Arf}(q_F^E)$
,
$\mathit{Arf}(q_F^E)$
,
![]() $0, 1$
, or undefined, does not depend on the choice of
$0, 1$
, or undefined, does not depend on the choice of
![]() $F$
.
$F$
.
Remark 3.2. If
![]() $E$
has odd cardinality, then the conclusion of the theorem does not hold unless we are in the classical case of
$E$
has odd cardinality, then the conclusion of the theorem does not hold unless we are in the classical case of
![]() $m=1$
.
$m=1$
.
Let us first sketch why, if
![]() $E$
consists of a singleton
$E$
consists of a singleton
![]() $\{\varepsilon \}$
, any
$\{\varepsilon \}$
, any
![]() $m$
-colored link
$m$
-colored link
![]() $L$
with
$L$
with
![]() $m\gt 1$
admits two totally connected C-complexes
$m\gt 1$
admits two totally connected C-complexes
![]() $F$
and
$F$
and
![]() $F'$
leading to quadratic forms
$F'$
leading to quadratic forms
![]() $q^E_F$
and
$q^E_F$
and
![]() $q^E_{F'}$
with different Arf invariants. Indeed, let us consider an arbitrary C-complex
$q^E_{F'}$
with different Arf invariants. Indeed, let us consider an arbitrary C-complex
![]() $F$
for
$F$
for
![]() $L$
, and let
$L$
, and let
![]() $F(\varepsilon )$
denote the oriented surface obtained from
$F(\varepsilon )$
denote the oriented surface obtained from
![]() $F$
by applying the transformation illustrated in Figure 5 to each clasp. There is a canonical isomorphism
$F$
by applying the transformation illustrated in Figure 5 to each clasp. There is a canonical isomorphism
![]() $H_1(F)\simeq H_1(F(\varepsilon ))$
yielding a congruence between the generalized Seifert form
$H_1(F)\simeq H_1(F(\varepsilon ))$
yielding a congruence between the generalized Seifert form
![]() $\alpha ^\varepsilon$
on
$\alpha ^\varepsilon$
on
![]() $F$
and the classical Seifert form
$F$
and the classical Seifert form
![]() $\alpha ^-$
on
$\alpha ^-$
on
![]() $F(\varepsilon )$
. As a consequence, we have
$F(\varepsilon )$
. As a consequence, we have
the classical Arf invariant of the oriented link
![]() $\partial F(\varepsilon )$
. Now, applying this transformation to two C-complexes
$\partial F(\varepsilon )$
. Now, applying this transformation to two C-complexes
![]() $F$
and
$F$
and
![]() $F'$
related by a move (T2) yields two links
$F'$
related by a move (T2) yields two links
![]() $\partial F(\varepsilon )$
and
$\partial F(\varepsilon )$
and
![]() $\partial F'(\varepsilon )$
which are related by a band move and the addition of an unknot, see Figure 6. This process enables us to produce two totally connected C-complexes for
$\partial F'(\varepsilon )$
which are related by a band move and the addition of an unknot, see Figure 6. This process enables us to produce two totally connected C-complexes for
![]() $L$
having Arf invariants with different values.
$L$
having Arf invariants with different values.
The general case of
![]() $E$
with odd cardinality is slightly more technical. As it turns out, one can show that any totally connected C-complex
$E$
with odd cardinality is slightly more technical. As it turns out, one can show that any totally connected C-complex
![]() $F_0$
such that
$F_0$
such that
![]() $\mathit{Arf}(q_{F_0}^E)$
is defined produces a link admitting two totally connected C-complexes
$\mathit{Arf}(q_{F_0}^E)$
is defined produces a link admitting two totally connected C-complexes
![]() $F$
and
$F$
and
![]() $F'$
with exactly one of
$F'$
with exactly one of
![]() $\mathit{Arf}(q^E_F)$
and
$\mathit{Arf}(q^E_F)$
and
![]() $\mathit{Arf}(q^E_{F'})$
defined. However, the details are rather cumbersome and will not be included in this note.
$\mathit{Arf}(q^E_{F'})$
defined. However, the details are rather cumbersome and will not be included in this note.
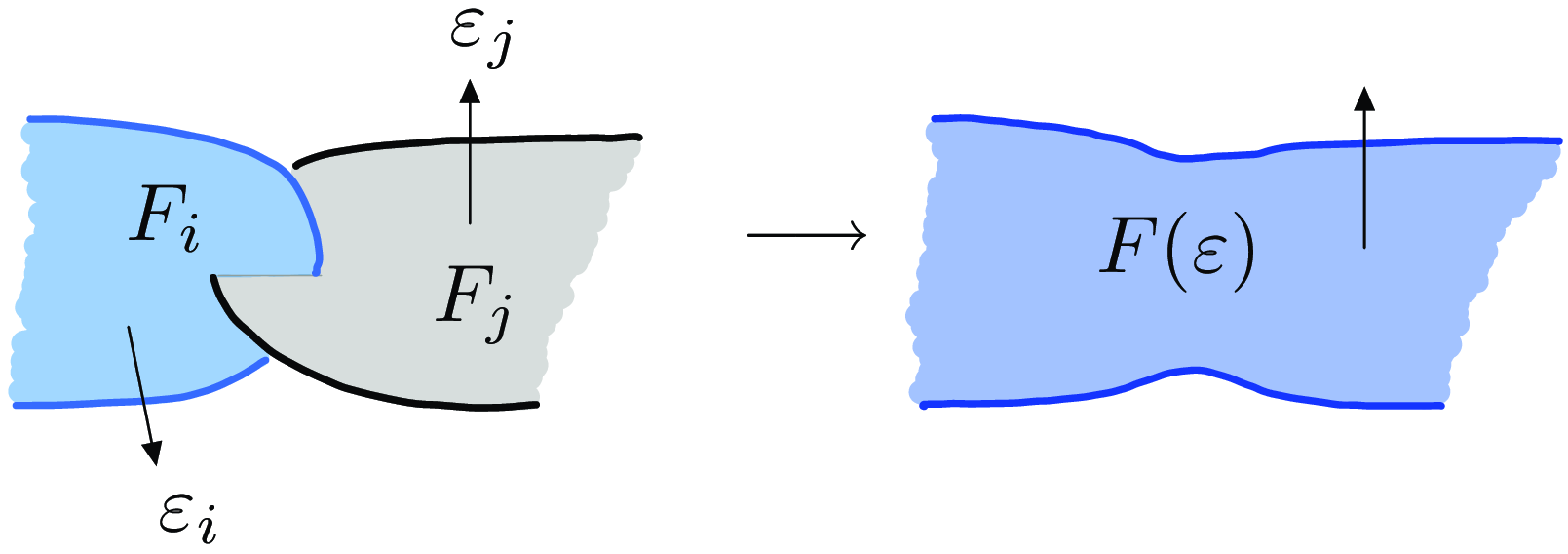
Figure 5. Transforming a C-complex
![]() $F$
into an oriented surface
$F$
into an oriented surface
![]() $F(\varepsilon )$
.
$F(\varepsilon )$
.
Remark 3.3. In general, Theorem 3.1 does not hold either without the assumption of total connectivity. For example, consider the two C-complexes
![]() $F$
and
$F$
and
![]() $F'$
illustrated in Figure 7 (left): they are related by a move (T3), recall Figure 8, and in particular yield isotopic colored links. However, the C-complex
$F'$
illustrated in Figure 7 (left): they are related by a move (T3), recall Figure 8, and in particular yield isotopic colored links. However, the C-complex
![]() $F'$
is not totally connected. Assuming that the components are ordered blue-black-red and that the left of Figure 7 shows the positive sides of the three surfaces, the choice
$F'$
is not totally connected. Assuming that the components are ordered blue-black-red and that the left of Figure 7 shows the positive sides of the three surfaces, the choice
![]() $E=\{+++,++-\}$
leads to a first quadratic form
$E=\{+++,++-\}$
leads to a first quadratic form
![]() $q^E_F$
which vanishes on
$q^E_F$
which vanishes on
![]() $\operatorname {rad}(B^E_F)$
, while the second quadratic form
$\operatorname {rad}(B^E_F)$
, while the second quadratic form
![]() $q^E_{F'}$
does not vanish on
$q^E_{F'}$
does not vanish on
![]() $\operatorname {rad}(B^E_{F'})$
. Hence, the value of
$\operatorname {rad}(B^E_{F'})$
. Hence, the value of
![]() $\mathit{Arf}(q_F^E)$
in general does depend on the choice of the C-complex
$\mathit{Arf}(q_F^E)$
in general does depend on the choice of the C-complex
![]() $F$
if is allowed not to be totally connected.
$F$
if is allowed not to be totally connected.
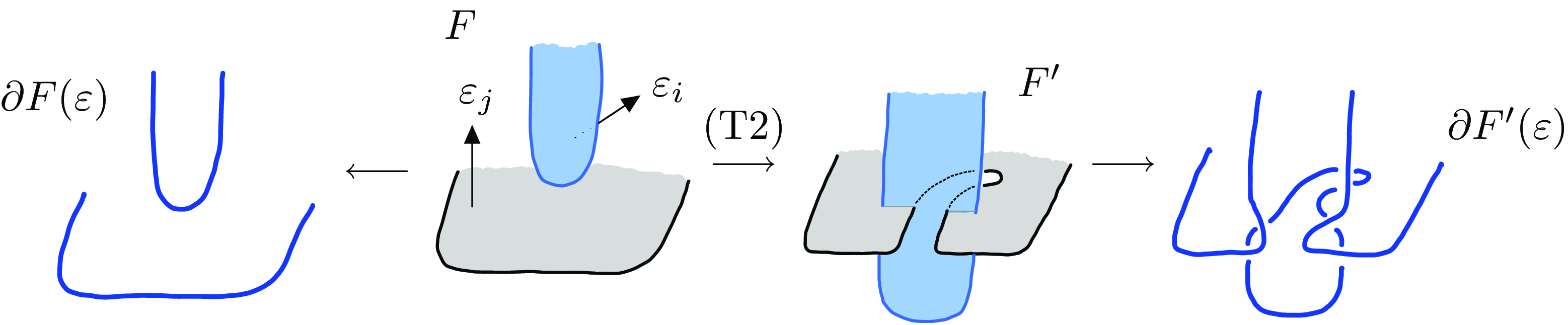
Figure 6. The links
![]() $\partial F(\varepsilon )$
and
$\partial F(\varepsilon )$
and
![]() $\partial F'(\varepsilon )$
obtained via
$\partial F'(\varepsilon )$
obtained via
![]() $F$
and
$F$
and
![]() $F'$
related by a move (T2).
$F'$
related by a move (T2).
We now present a couple of easy examples.
Example 3.4. Let us focus on the case of
![]() $2$
colors. Because of the equality
$2$
colors. Because of the equality
![]() $A^{-\varepsilon }=(A^\varepsilon )^{{\operatorname {T}}}$
, a choice of
$A^{-\varepsilon }=(A^\varepsilon )^{{\operatorname {T}}}$
, a choice of
![]() $E$
in
$E$
in
![]() $\{\{++,-\,-\},\{+-,-+\},\{++,+-,-+,-\,-\}\}$
yields a trivial invariant
$\{\{++,-\,-\},\{+-,-+\},\{++,+-,-+,-\,-\}\}$
yields a trivial invariant
![]() $\mathit{Arf}_{\!E}\equiv 0$
, and the same obviously holds for
$\mathit{Arf}_{\!E}\equiv 0$
, and the same obviously holds for
![]() $E=\emptyset$
. For the same reason, we have
$E=\emptyset$
. For the same reason, we have
![]() $\mathit{Arf}_{\!E}\equiv \mathit{Arf}_{\!-E}$
, where
$\mathit{Arf}_{\!E}\equiv \mathit{Arf}_{\!-E}$
, where
![]() $-E$
denotes the set
$-E$
denotes the set
![]() $E$
with all signs changed. Hence, we are left with
$E$
with all signs changed. Hence, we are left with
![]() $E=\{++,+-\}$
and
$E=\{++,+-\}$
and
![]() $\{++,-+\}$
yielding potentially non-trivial invariants.
$\{++,-+\}$
yielding potentially non-trivial invariants.
First, consider the 2-colored link
![]() $L$
given by the (positive or negative) Hopf link. As illustrated in the right of Figure 7, it admits a contractible C-complex
$L$
given by the (positive or negative) Hopf link. As illustrated in the right of Figure 7, it admits a contractible C-complex
![]() $F$
; therefore, we get
$F$
; therefore, we get
![]() $\mathit{Arf}_{\!E}(L)=0$
.
$\mathit{Arf}_{\!E}(L)=0$
.
Then, let
![]() $L'$
denote the 2-colored link given by the
$L'$
denote the 2-colored link given by the
![]() $(2,4)$
-torus link. The C-complex
$(2,4)$
-torus link. The C-complex
![]() $F'$
illustrated in the right of Figure 7 leads to
$F'$
illustrated in the right of Figure 7 leads to
![]() $A^{++}=A^{-\,-}=(-1)$
and
$A^{++}=A^{-\,-}=(-1)$
and
![]() $A^{+-}=A^{-+}=(0)$
. Hence, the signs
$A^{+-}=A^{-+}=(0)$
. Hence, the signs
![]() $E=\{++,+-\}$
and
$E=\{++,+-\}$
and
![]() $\{++,-+\}$
give the matrices
$\{++,-+\}$
give the matrices
![]() $A^E=(1)$
and
$A^E=(1)$
and
![]() $B^E=(0)$
, so we get
$B^E=(0)$
, so we get
![]() $\mathit{Arf}_{\!E}(L')$
undefined.
$\mathit{Arf}_{\!E}(L')$
undefined.
Finally, let
![]() $L''$
denote the
$L''$
denote the
![]() $(2,6)$
-torus link. The C-complex
$(2,6)$
-torus link. The C-complex
![]() $F''$
together with the basis of
$F''$
together with the basis of
![]() $H_1(F'')$
illustrated in the right of Figure 7 yield the generalized Seifert matrices
$H_1(F'')$
illustrated in the right of Figure 7 yield the generalized Seifert matrices
![]() $A^{++}=(A^{-\,-})^{{\operatorname {T}}}=\left (\begin{smallmatrix}-1&0\\ -1&-1\end{smallmatrix}\right )$
and
$A^{++}=(A^{-\,-})^{{\operatorname {T}}}=\left (\begin{smallmatrix}-1&0\\ -1&-1\end{smallmatrix}\right )$
and
![]() $A^{+-}=A^{-+}=\left (\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right )$
. Both choices
$A^{+-}=A^{-+}=\left (\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right )$
. Both choices
![]() $E=\{++,+-\}$
and
$E=\{++,+-\}$
and
![]() $\{++,-+\}$
lead to the matrices
$\{++,-+\}$
lead to the matrices
![]() $A^E=\left (\begin{smallmatrix}1&0\\ 1&1\end{smallmatrix}\right )$
and
$A^E=\left (\begin{smallmatrix}1&0\\ 1&1\end{smallmatrix}\right )$
and
![]() $B^E=\left (\begin{smallmatrix}0&1\\ 1&0\end{smallmatrix}\right )$
, so we get
$B^E=\left (\begin{smallmatrix}0&1\\ 1&0\end{smallmatrix}\right )$
, so we get
![]() $\mathit{Arf}_{\!E}(L'')=1$
, for example using Equation (1).
$\mathit{Arf}_{\!E}(L'')=1$
, for example using Equation (1).
3.2. Proof of Theorem3.1
Let us fix an
![]() $m$
-colored link
$m$
-colored link
![]() $L$
with
$L$
with
![]() $m\gt 1$
and a subset
$m\gt 1$
and a subset
![]() $E\subset \{\pm \}^m$
of even cardinality. We want to show that if
$E\subset \{\pm \}^m$
of even cardinality. We want to show that if
![]() $F$
and
$F$
and
![]() $F'$
are two totally connected C-complexes for
$F'$
are two totally connected C-complexes for
![]() $L$
, then the values of
$L$
, then the values of
![]() $\mathit{Arf}(q^E_F)$
and of
$\mathit{Arf}(q^E_F)$
and of
![]() $\mathit{Arf}(q^E_{F'})$
coincide.
$\mathit{Arf}(q^E_{F'})$
coincide.
The most natural and direct way to show this result is to use the four transformations involved in the generalized S-equivalence of Appendix A. Instead, we will make use of the following lemma which introduces a new move (T5): this allows to reduce the number of transformations from four to three, thus yielding a slightly shorter proof of Theorem3.1. Note, however, that this new move might change the isotopy type of the underlying colored link and can therefore not be used for generalized S-equivalence.
Lemma 3.5. Let
![]() $F$
and
$F$
and
![]() $F'$
be two totally connected C-complexes and
$F'$
be two totally connected C-complexes and
![]() $E\subset \{\pm \}^m$
of even cardinality. If
$E\subset \{\pm \}^m$
of even cardinality. If
![]() $F$
and
$F$
and
![]() $F'$
are related by the move (T5) described in Figure 9, then the values of
$F'$
are related by the move (T5) described in Figure 9, then the values of
![]() $\mathit{Arf}(q_F^E)$
and of
$\mathit{Arf}(q_F^E)$
and of
![]() $\mathit{Arf}(q^E_{F'})$
coincide.
$\mathit{Arf}(q^E_{F'})$
coincide.
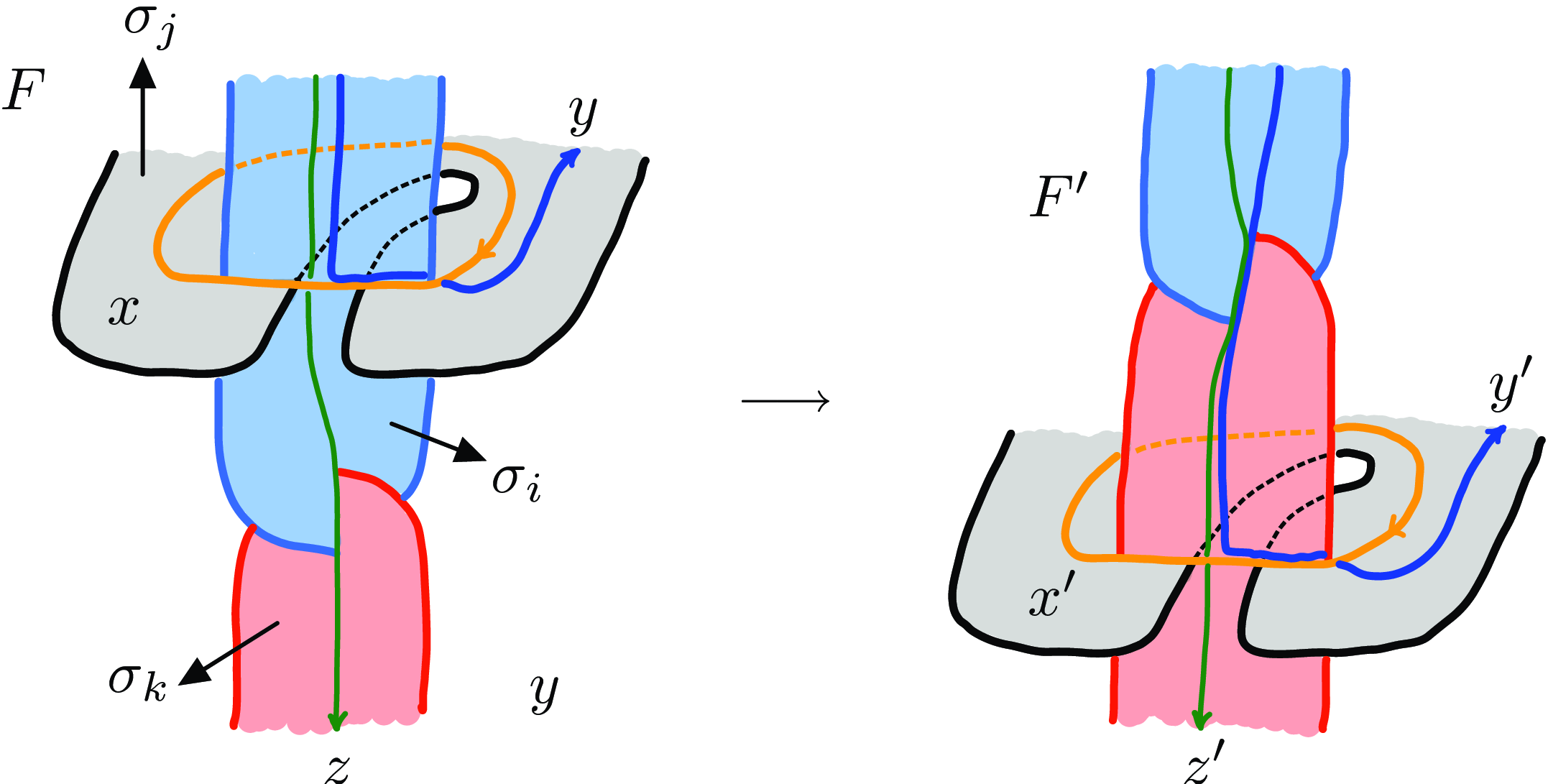
Figure 8. The surfaces and cycles involved in the move (T3).
We will first introduce some notation, then prove Theorem3.1 assuming Lemma 3.5, and finally check this lemma.
Notation 3.6. Given
![]() $E\subset \{\pm \}^m$
and a fixed color
$E\subset \{\pm \}^m$
and a fixed color
![]() $i$
and sign
$i$
and sign
![]() $\sigma$
, we write
$\sigma$
, we write
![]() $n_i^\sigma$
for the cardinality of
$n_i^\sigma$
for the cardinality of
![]() $\{\varepsilon \in E\,|\,\varepsilon _i=\sigma \}$
. Similarly, given signs
$\{\varepsilon \in E\,|\,\varepsilon _i=\sigma \}$
. Similarly, given signs
![]() $\sigma ,\tau$
and colors
$\sigma ,\tau$
and colors
![]() $i,j$
, we denote by
$i,j$
, we denote by
![]() $n_{ij}^{\sigma \tau }$
the cardinality of
$n_{ij}^{\sigma \tau }$
the cardinality of
![]() $\{\varepsilon \in E\,|\,\varepsilon _i=\sigma ,\,\varepsilon _j=\tau \}$
.
$\{\varepsilon \in E\,|\,\varepsilon _i=\sigma ,\,\varepsilon _j=\tau \}$
.
Proof of Theorem 3.1. By Lemma 2.5, we only need to show that if a totally connected C-complex
![]() $F'$
is obtained from another totally connected C-complex
$F'$
is obtained from another totally connected C-complex
![]() $F$
by one of the movements (T0)–(T4), then the values
$F$
by one of the movements (T0)–(T4), then the values
![]() $\mathit{Arf}(q^E_{F})$
and
$\mathit{Arf}(q^E_{F})$
and
![]() $\mathit{Arf}(q^E_{F'})$
coincide.
$\mathit{Arf}(q^E_{F'})$
coincide.
Since (T0) is an ambient isotopy, the equality is automatically satisfied. The moves (T2) and (T3) being compositions of (T0) and (T5), Lemma 3.5 implies that they do not change the value of the Arf invariant.
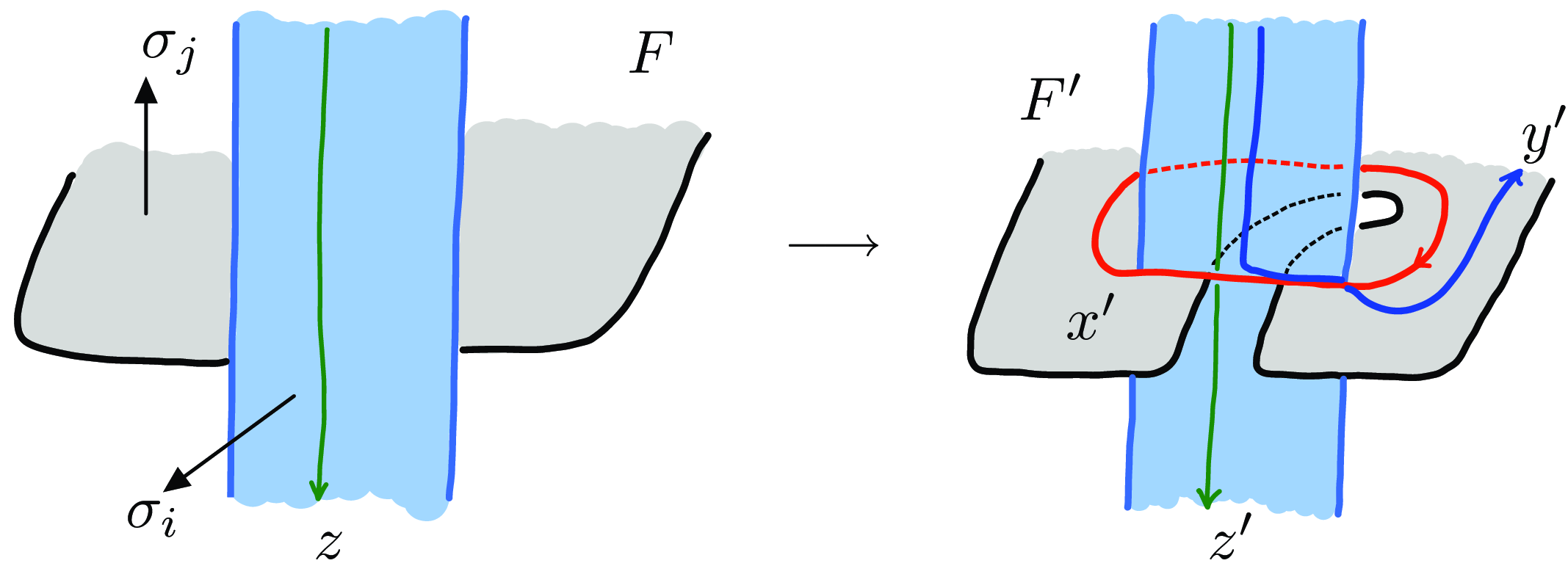
Figure 9. The move (T5).
Let us now suppose that, for some
![]() $1\le i\le m$
and
$1\le i\le m$
and
![]() $\sigma _i\in \{\pm \}$
, the C-complex
$\sigma _i\in \{\pm \}$
, the C-complex
![]() $F'$
is obtained from
$F'$
is obtained from
![]() $F$
by a move (T1) on the
$F$
by a move (T1) on the
![]() $\sigma _i$
-side of
$\sigma _i$
-side of
![]() $F_i$
. By Equation (A.1), the sums of generalized Seifert matrices
$F_i$
. By Equation (A.1), the sums of generalized Seifert matrices
![]() $A^E_F=\sum _{\varepsilon \in E} A^\varepsilon _F$
and
$A^E_F=\sum _{\varepsilon \in E} A^\varepsilon _F$
and
![]() $A^E_{F'}=\sum _{\varepsilon \in E} A^\varepsilon _{F'}$
are related by
$A^E_{F'}=\sum _{\varepsilon \in E} A^\varepsilon _{F'}$
are related by
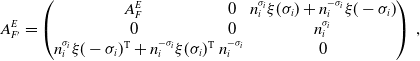 \begin{equation*} A_{F'}^E=\begin{pmatrix} A^E_F & 0 & n_i^{\sigma _i}\xi (\sigma _i)+n_i^{-\sigma _i}\xi (-\sigma _i)\\ 0 & 0 & n_i^{\sigma _i}\\ n_i^{\sigma _i}\xi (-\sigma _i)^{{\operatorname {T}}}+n_i^{-\sigma _i}\xi (\sigma _i)^{{\operatorname {T}}} & n_i^{-\sigma _i} & 0 \end{pmatrix}\,, \end{equation*}
\begin{equation*} A_{F'}^E=\begin{pmatrix} A^E_F & 0 & n_i^{\sigma _i}\xi (\sigma _i)+n_i^{-\sigma _i}\xi (-\sigma _i)\\ 0 & 0 & n_i^{\sigma _i}\\ n_i^{\sigma _i}\xi (-\sigma _i)^{{\operatorname {T}}}+n_i^{-\sigma _i}\xi (\sigma _i)^{{\operatorname {T}}} & n_i^{-\sigma _i} & 0 \end{pmatrix}\,, \end{equation*}
assuming Notation 3.6. Since
![]() $E$
is of even cardinality, the integers
$E$
is of even cardinality, the integers
![]() $n_i^{\sigma _i}$
and
$n_i^{\sigma _i}$
and
![]() $n_i^{-\sigma _i}$
have the same parity, so the associated bilinear forms satisfy
$n_i^{-\sigma _i}$
have the same parity, so the associated bilinear forms satisfy
![]() $B_{F'}^E = B_F^E \oplus \left (\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right )$
. In other words, we have
$B_{F'}^E = B_F^E \oplus \left (\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right )$
. In other words, we have
![]() $\operatorname {rad}(B_{F'}^E)=\operatorname {rad}(B_F^E)\oplus \mathbb{Z}_2 x\oplus \mathbb{Z}_2 y$
, with
$\operatorname {rad}(B_{F'}^E)=\operatorname {rad}(B_F^E)\oplus \mathbb{Z}_2 x\oplus \mathbb{Z}_2 y$
, with
![]() $x,y$
corresponding to the final two rows and columns in
$x,y$
corresponding to the final two rows and columns in
![]() $A_{F'}^E$
. Since
$A_{F'}^E$
. Since
![]() $q^E_{F'}(x)=q^E_{F'}(y)=0$
, the Arf invariants of
$q^E_{F'}(x)=q^E_{F'}(y)=0$
, the Arf invariants of
![]() $q^E_{F'}$
and of
$q^E_{F'}$
and of
![]() $q^E_{F}$
have the same value.
$q^E_{F}$
have the same value.
Finally, the move (T4) can be obtained as follows: first use an ambient isotopy (twisting the vertical band) to get the arc into one of the two situations illustrated in the left and center of Figure 4, then (if needed) use the inverse of
![]() $\mathrm{(T4_a)}$
to get to the center of this figure, then move (T5), then an ambient isotopy to untwist the vertical band, and finally the inverse of (T5) to get the arc into standard position. Thus, the invariance under a general move (T4) can be reduced to the invariance under the specific move
$\mathrm{(T4_a)}$
to get to the center of this figure, then move (T5), then an ambient isotopy to untwist the vertical band, and finally the inverse of (T5) to get the arc into standard position. Thus, the invariance under a general move (T4) can be reduced to the invariance under the specific move
![]() $\mathrm{(T4_a)}$
. If
$\mathrm{(T4_a)}$
. If
![]() $F'$
is obtained from
$F'$
is obtained from
![]() $F$
via such a move, then Equations (A.2) and (A.3) imply that the generalized Seifert matrices
$F$
via such a move, then Equations (A.2) and (A.3) imply that the generalized Seifert matrices
![]() $A^\varepsilon _F$
and
$A^\varepsilon _F$
and
![]() $A^\varepsilon _{F'}$
have identical diagonals (recall that we have
$A^\varepsilon _{F'}$
have identical diagonals (recall that we have
![]() $n=0$
), and satisfy
$n=0$
), and satisfy
for all
![]() $\varepsilon \in \{\pm \}^m$
. Thus, any combination of these matrices leads to the same Arf invariant.
$\varepsilon \in \{\pm \}^m$
. Thus, any combination of these matrices leads to the same Arf invariant.
This concludes the proof of Theorem3.1, assuming Lemma 3.5 whose demonstration we now present.
Proof of Lemma 3.5
. Let us fix two totally connected C-complexes
![]() $F$
and
$F$
and
![]() $F'$
that are related by the move (T5) illustrated in Figure 9, whose notation we assume. Since
$F'$
that are related by the move (T5) illustrated in Figure 9, whose notation we assume. Since
![]() $F$
is totally connected, we have
$F$
is totally connected, we have
![]() $H_1(F')=H_1(F)\oplus \mathbb{Z} x'\oplus \mathbb{Z} y'$
, with
$H_1(F')=H_1(F)\oplus \mathbb{Z} x'\oplus \mathbb{Z} y'$
, with
![]() $x',y'\subset F_i\cup F_j$
the cycles represented in the right side of Figure 9. Up to a move (T1) along
$x',y'\subset F_i\cup F_j$
the cycles represented in the right side of Figure 9. Up to a move (T1) along
![]() $F_i$
if needed, a basis of
$F_i$
if needed, a basis of
![]() $F$
can be chosen to contain a unique cycle
$F$
can be chosen to contain a unique cycle
![]() $z$
as in Figure 9. Consider the symbols
$z$
as in Figure 9. Consider the symbols
![]() $\delta$
and
$\delta$
and
![]() $\chi$
introduced in Notation A.2. In the appropriate bases, the generalized Seifert matrix
$\chi$
introduced in Notation A.2. In the appropriate bases, the generalized Seifert matrix
![]() $A^\varepsilon _{F'}$
is obtained from
$A^\varepsilon _{F'}$
is obtained from
![]() $A^\varepsilon _F$
via
$A^\varepsilon _F$
via
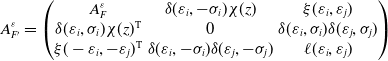 \begin{equation*} A^\varepsilon _{F'}=\begin{pmatrix} A^\varepsilon _F & \delta (\varepsilon _i,-\sigma _i)\chi (z) & \xi (\varepsilon _i,\varepsilon _j)\\ \delta (\varepsilon _i,\sigma _i)\chi (z)^{{\operatorname {T}}} & 0 & \delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}} & \delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i,\varepsilon _j) \end{pmatrix}\, \end{equation*}
\begin{equation*} A^\varepsilon _{F'}=\begin{pmatrix} A^\varepsilon _F & \delta (\varepsilon _i,-\sigma _i)\chi (z) & \xi (\varepsilon _i,\varepsilon _j)\\ \delta (\varepsilon _i,\sigma _i)\chi (z)^{{\operatorname {T}}} & 0 & \delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}} & \delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i,\varepsilon _j) \end{pmatrix}\, \end{equation*}
with
![]() $\ell (-\varepsilon _i,-\varepsilon _j)=\ell (\varepsilon _i,\varepsilon _j)\in \mathbb{Z}$
and
$\ell (-\varepsilon _i,-\varepsilon _j)=\ell (\varepsilon _i,\varepsilon _j)\in \mathbb{Z}$
and
![]() $\xi (\varepsilon _i,\varepsilon _j)$
some integral vector only depending on
$\xi (\varepsilon _i,\varepsilon _j)$
some integral vector only depending on
![]() $\varepsilon _i$
and
$\varepsilon _i$
and
![]() $\varepsilon _j$
.
$\varepsilon _j$
.
Assuming Notation 3.6 and setting
this leads to
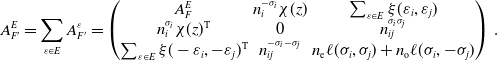 \begin{equation} A^E_{F'}=\sum _{\varepsilon \in E}A^{\varepsilon }_{F'}=\begin{pmatrix} A^E_F&n_i^{-\sigma _i}\chi (z)& \sum _{\varepsilon \in E}\xi (\varepsilon _i,\varepsilon _j)\\ n_i^{\sigma _i}\chi (z)^{{\operatorname {T}}}&0&n_{ij}^{\sigma _i\sigma _j}\\ \sum _{\varepsilon \in E}\xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}}&n_{ij}^{-\sigma _i-\sigma _j}& n_{\text{e}}\ell (\sigma _i,\sigma _j)+n_{\text{o}}\ell (\sigma _i,-\sigma _j)\end{pmatrix}\,. \end{equation}
\begin{equation} A^E_{F'}=\sum _{\varepsilon \in E}A^{\varepsilon }_{F'}=\begin{pmatrix} A^E_F&n_i^{-\sigma _i}\chi (z)& \sum _{\varepsilon \in E}\xi (\varepsilon _i,\varepsilon _j)\\ n_i^{\sigma _i}\chi (z)^{{\operatorname {T}}}&0&n_{ij}^{\sigma _i\sigma _j}\\ \sum _{\varepsilon \in E}\xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}}&n_{ij}^{-\sigma _i-\sigma _j}& n_{\text{e}}\ell (\sigma _i,\sigma _j)+n_{\text{o}}\ell (\sigma _i,-\sigma _j)\end{pmatrix}\,. \end{equation}
By assumption, the integer
![]() $n_i^{\sigma _i}+n_i^{-\sigma _i}=\vert E\vert$
is even, yielding
$n_i^{\sigma _i}+n_i^{-\sigma _i}=\vert E\vert$
is even, yielding
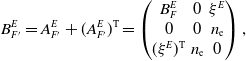 \begin{equation*} B^E_{F'}=A^E_{F'}+(A^E_{F'})^{{\operatorname {T}}}=\begin{pmatrix} B^E_F&0&\xi ^E\\ 0&0&n_{\text{e}}\\ (\xi ^E)^{{\operatorname {T}}}&n_{\text{e}}&0\end{pmatrix}, \end{equation*}
\begin{equation*} B^E_{F'}=A^E_{F'}+(A^E_{F'})^{{\operatorname {T}}}=\begin{pmatrix} B^E_F&0&\xi ^E\\ 0&0&n_{\text{e}}\\ (\xi ^E)^{{\operatorname {T}}}&n_{\text{e}}&0\end{pmatrix}, \end{equation*}
where
Since
is even, the two integers
![]() $n_{\text{e}}$
and
$n_{\text{e}}$
and
![]() $n_{\text{o}}$
have the same parity. If it is even, then by the computations above, we have
$n_{\text{o}}$
have the same parity. If it is even, then by the computations above, we have
![]() $B^E_{F'}=B^E_F\oplus \left (\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right )$
while the matrix
$B^E_{F'}=B^E_F\oplus \left (\begin{smallmatrix}0&0\\ 0&0\end{smallmatrix}\right )$
while the matrix
![]() $A^E_{F'}$
is of the form
$A^E_{F'}$
is of the form
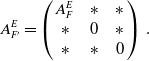 \begin{equation*} A^E_{F'}=\left(\begin{array}{c@{\quad}c@{\quad}c} A^E_F& \ast &\ast \\ \ast &0&\ast \\ \ast &\ast &0\end{array}\right)\,. \end{equation*}
\begin{equation*} A^E_{F'}=\left(\begin{array}{c@{\quad}c@{\quad}c} A^E_F& \ast &\ast \\ \ast &0&\ast \\ \ast &\ast &0\end{array}\right)\,. \end{equation*}
The values of
![]() $\mathit{Arf}(q^E_{F'})$
and
$\mathit{Arf}(q^E_{F'})$
and
![]() $\mathit{Arf}(q^E_F)$
are then easily seen to coincide, as in the proof of the invariance under move (T1) above. If
$\mathit{Arf}(q^E_F)$
are then easily seen to coincide, as in the proof of the invariance under move (T1) above. If
![]() $n_{\text{e}}$
and
$n_{\text{e}}$
and
![]() $n_{\text{o}}$
are odd, then the matrix
$n_{\text{o}}$
are odd, then the matrix
![]() $B^E_{F'}$
is of the form
$B^E_{F'}$
is of the form
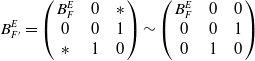 \begin{equation} B^E_{F'}=\left(\begin{array}{c@{\quad}c@{\quad}c} B^E_F& 0&\ast \\ 0&0&1\\ \ast &1&0\end{array}\right)\sim \left(\begin{array}{c@{\quad}c@{\quad}c} B^E_F& 0&0\\ 0&0&1\\0&1&0\end{array}\right) \end{equation}
\begin{equation} B^E_{F'}=\left(\begin{array}{c@{\quad}c@{\quad}c} B^E_F& 0&\ast \\ 0&0&1\\ \ast &1&0\end{array}\right)\sim \left(\begin{array}{c@{\quad}c@{\quad}c} B^E_F& 0&0\\ 0&0&1\\0&1&0\end{array}\right) \end{equation}
with
![]() $\sim$
standing for congruence, leading to
$\sim$
standing for congruence, leading to
![]() $\operatorname {rad}(B^E_{F'})=\operatorname {rad}(B^E_F)\subset H_1(F;\,\mathbb{Z}_2)$
. By (2), the restriction of
$\operatorname {rad}(B^E_{F'})=\operatorname {rad}(B^E_F)\subset H_1(F;\,\mathbb{Z}_2)$
. By (2), the restriction of
![]() $q^E_{F'}$
to
$q^E_{F'}$
to
![]() $H_1(F;\,\mathbb{Z}_2)$
coincides with
$H_1(F;\,\mathbb{Z}_2)$
coincides with
![]() $q^E_{F}$
, so
$q^E_{F}$
, so
![]() $q^E_{F'}$
vanishes on
$q^E_{F'}$
vanishes on
![]() $\operatorname {rad}(B^E_{F'})$
if and only if
$\operatorname {rad}(B^E_{F'})$
if and only if
![]() $q^E_{F}$
vanishes on
$q^E_{F}$
vanishes on
![]() $\operatorname {rad}(B^E_{F})$
. Let us assume that this is the case, so that neither
$\operatorname {rad}(B^E_{F})$
. Let us assume that this is the case, so that neither
![]() $\mathit{Arf}(q^E_{F'})$
nor
$\mathit{Arf}(q^E_{F'})$
nor
![]() $\mathit{Arf}(q^E_{F})$
is undefined. By Equation (3), if
$\mathit{Arf}(q^E_{F})$
is undefined. By Equation (3), if
![]() $(a_k)_k$
is a basis of
$(a_k)_k$
is a basis of
![]() $H_1(F;\,\mathbb{Z}_2)/\operatorname {rad}(B^E_{F})$
which is symplectic with respect to
$H_1(F;\,\mathbb{Z}_2)/\operatorname {rad}(B^E_{F})$
which is symplectic with respect to
![]() $B^E_F$
, then a basis of
$B^E_F$
, then a basis of
![]() $H_1(F';\,\,\mathbb{Z}_2)/\operatorname {rad}(B^E_{F'})$
which is symplectic with respect to
$H_1(F';\,\,\mathbb{Z}_2)/\operatorname {rad}(B^E_{F'})$
which is symplectic with respect to
![]() $B^E_{F'}$
is given by
$B^E_{F'}$
is given by
![]() $(a'_k)_k\cup (x,y)$
, with
$(a'_k)_k\cup (x,y)$
, with
![]() $a'_k\in \{a_k, a_k+x\}$
. By (2), we have
$a'_k\in \{a_k, a_k+x\}$
. By (2), we have
![]() $q^E_{F'}(x)=0$
and
$q^E_{F'}(x)=0$
and
![]() $q^E_{F'}(a_k')=q^E_F(a_k)$
for all
$q^E_{F'}(a_k')=q^E_F(a_k)$
for all
![]() $k$
. Equation (1) now implies that
$k$
. Equation (1) now implies that
![]() $\mathit{Arf}(q^E_{F'})$
and
$\mathit{Arf}(q^E_{F'})$
and
![]() $\mathit{Arf}(q^E_{F})$
coincide.
$\mathit{Arf}(q^E_{F})$
coincide.
4. Determination by linking numbers
The aim of this last section is to give the proof of Proposition 1.2, whose statement we recall for the reader’s convenience.
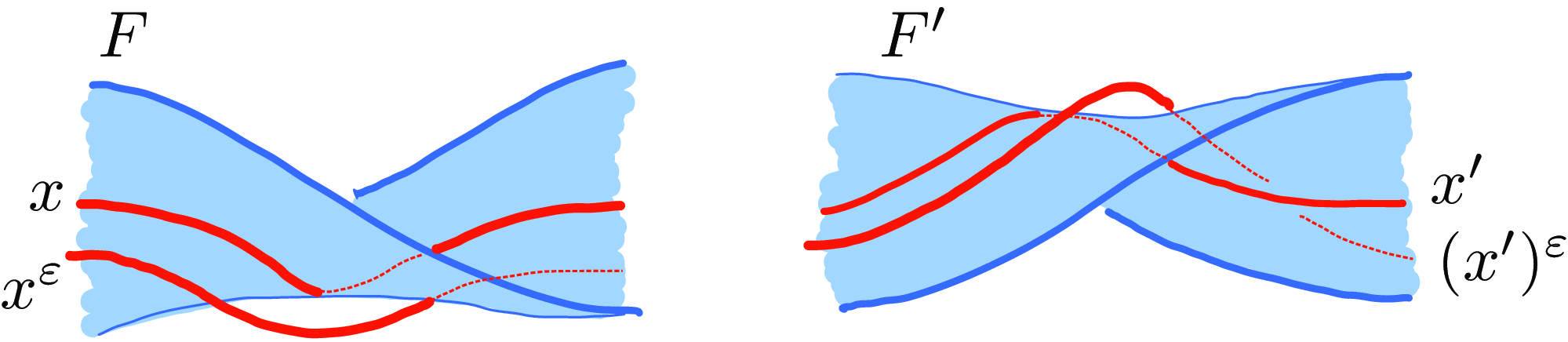
Figure 10. A crossing change between two strands of the same color is realized by twisting a band.

Figure 11. A crossing change between two strands of different colors can be realized by adding a clasp.
Proposition 4.1. For any
![]() $m$
-colored link
$m$
-colored link
![]() $L$
and any
$L$
and any
![]() $E\subset \{\pm \}^m$
of even cardinality, the value of
$E\subset \{\pm \}^m$
of even cardinality, the value of
![]() $\mathit{Arf}_{\!E}(L)$
is determined by the linking numbers of the components of
$\mathit{Arf}_{\!E}(L)$
is determined by the linking numbers of the components of
![]() $L$
.
$L$
.
Our proof of this result relies on four lemmas. The first one is best formulated using the following terminology: two colored links are said to be homotopic if they can be related by isotopies (preserving the orientation and color of each component) and crossing changes between strands of the same color. This first lemma states that generalized Arf invariants are invariant under homotopy of colored links.
Lemma 4.2. If
![]() $L$
and
$L$
and
![]() $L'$
are homotopic
$L'$
are homotopic
![]() $m$
-colored links, then for any
$m$
-colored links, then for any
![]() $E\subset \{\pm \}^m$
of even cardinality, we have
$E\subset \{\pm \}^m$
of even cardinality, we have
![]() $\mathit{Arf}_{\!E}(L)=\mathit{Arf}_{\!E}(L')$
.
$\mathit{Arf}_{\!E}(L)=\mathit{Arf}_{\!E}(L')$
.
Proof. Any crossing change between two strands of the same color can be realised by adding a full twist to a band in a C-complex, as illustrated in Figure 10. Writing
![]() $F$
and
$F$
and
![]() $F'$
for the corresponding C-complexes, one immediately sees that the groups
$F'$
for the corresponding C-complexes, one immediately sees that the groups
![]() $H_1(F;\,\mathbb{Z}_2)$
and
$H_1(F;\,\mathbb{Z}_2)$
and
![]() $H_1(F';\,\mathbb{Z}_2)$
are canonically isomorphic; let us denote by
$H_1(F';\,\mathbb{Z}_2)$
are canonically isomorphic; let us denote by
![]() $x'\in H_1(F';\,\mathbb{Z}_2)$
the image under this isomorphism of an arbitrary cycle
$x'\in H_1(F';\,\mathbb{Z}_2)$
the image under this isomorphism of an arbitrary cycle
![]() $x$
in
$x$
in
![]() $F$
. We will now check that
$F$
. We will now check that
![]() $q^E_{F}(x)=q^E_{F'}(x')$
for any
$q^E_{F}(x)=q^E_{F'}(x')$
for any
![]() $x\in H_1(F;\,\mathbb{Z}_2)$
, which implies the statement of the lemma. Consider an arbitrary class in
$x\in H_1(F;\,\mathbb{Z}_2)$
, which implies the statement of the lemma. Consider an arbitrary class in
![]() $H_1(F;\,\mathbb{Z}_2)$
. Since we are working modulo 2, this class is represented by a cycle
$H_1(F;\,\mathbb{Z}_2)$
. Since we are working modulo 2, this class is represented by a cycle
![]() $x\subset F$
which is either supported outside the part of
$x\subset F$
which is either supported outside the part of
![]() $F$
depicted in Figure 10, or crosses this band once. In the first case, we clearly have
$F$
depicted in Figure 10, or crosses this band once. In the first case, we clearly have
![]() $q^\varepsilon _{F}(x)=q^\varepsilon _{F'}(x')$
for all
$q^\varepsilon _{F}(x)=q^\varepsilon _{F'}(x')$
for all
![]() $\varepsilon$
and the equality
$\varepsilon$
and the equality
![]() $q^E_{F}(x)=q^E_{F'}(x')$
holds trivially. In the second, and for any choice of signs
$q^E_{F}(x)=q^E_{F'}(x')$
holds trivially. In the second, and for any choice of signs
![]() $\varepsilon \in \{\pm \}^m$
, we have the modulo 2 equality
$\varepsilon \in \{\pm \}^m$
, we have the modulo 2 equality
see Figure 10. Since this holds for all
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $E$
is even, the equality
$E$
is even, the equality
![]() $q^E_{F}(x)=q^E_{F'}(x')$
follows.
$q^E_{F}(x)=q^E_{F'}(x')$
follows.
Before stating the next lemma, recall that
![]() $n_{ij}^{\sigma \tau }$
denotes the cardinality of
$n_{ij}^{\sigma \tau }$
denotes the cardinality of
![]() $\{\varepsilon \in E\,|\,\varepsilon _i=\sigma ,\,\varepsilon _j=\tau \}$
.
$\{\varepsilon \in E\,|\,\varepsilon _i=\sigma ,\,\varepsilon _j=\tau \}$
.
Lemma 4.3. Let
![]() $E\subset \{\pm \}^m$
be a set of even cardinality and
$E\subset \{\pm \}^m$
be a set of even cardinality and
![]() $i,j$
be colors such that
$i,j$
be colors such that
![]() $n_{ij}^{++}$
and
$n_{ij}^{++}$
and
![]() $n_{ij}^{-\,-}$
have the same parity. Then, given any colored links
$n_{ij}^{-\,-}$
have the same parity. Then, given any colored links
![]() $L,L'$
related by a crossing change between components of colors
$L,L'$
related by a crossing change between components of colors
![]() $i$
and
$i$
and
![]() $j$
, we have
$j$
, we have
![]() $\mathit{Arf}_{\!E}(L)=\mathit{Arf}_{\!E}(L')$
.
$\mathit{Arf}_{\!E}(L)=\mathit{Arf}_{\!E}(L')$
.
Proof. First note that if the colors
![]() $i$
and
$i$
and
![]() $j$
coincide (a case that was not ruled out explicitly), then we have
$j$
coincide (a case that was not ruled out explicitly), then we have
![]() $n_{ii}^{++}+n_{ii}^{-\,-}=\vert E\vert$
even, so the assumption is always verified, and the conclusion holds by Lemma 4.2. Therefore, we can now assume that
$n_{ii}^{++}+n_{ii}^{-\,-}=\vert E\vert$
even, so the assumption is always verified, and the conclusion holds by Lemma 4.2. Therefore, we can now assume that
![]() $i$
and
$i$
and
![]() $j$
are distinct colors. Any crossing change between two strands of different colors can be realised by adding a clasp in a C-complex, as illustrated in Figure 11. Assuming the notations
$j$
are distinct colors. Any crossing change between two strands of different colors can be realised by adding a clasp in a C-complex, as illustrated in Figure 11. Assuming the notations
![]() $F,F'$
of this figure, and using the fact that
$F,F'$
of this figure, and using the fact that
![]() $F$
is connected, we get a natural isomorphism
$F$
is connected, we get a natural isomorphism
![]() $H_1(F';\,\mathbb{Z}_2)\simeq H_1(F;\,\mathbb{Z}_2)\oplus \mathbb{Z}_2 y$
, with
$H_1(F';\,\mathbb{Z}_2)\simeq H_1(F;\,\mathbb{Z}_2)\oplus \mathbb{Z}_2 y$
, with
![]() $y$
a cycle passing through the newly created clasp. Moreover, since
$y$
a cycle passing through the newly created clasp. Moreover, since
![]() $F$
is totally connected, one can assume that
$F$
is totally connected, one can assume that
![]() $y$
is contained in
$y$
is contained in
![]() $F_i\cup F_j$
. Expressed in coherent bases, the generalized Seifert matrices are related by
$F_i\cup F_j$
. Expressed in coherent bases, the generalized Seifert matrices are related by
with
![]() $\ell (\varepsilon _i,\varepsilon _j)=\ell (-\varepsilon _i,-\varepsilon _j)\in \mathbb{Z}$
and
$\ell (\varepsilon _i,\varepsilon _j)=\ell (-\varepsilon _i,-\varepsilon _j)\in \mathbb{Z}$
and
![]() $\xi (\varepsilon _i,\varepsilon _j)$
some integral vector which only depends on
$\xi (\varepsilon _i,\varepsilon _j)$
some integral vector which only depends on
![]() $\varepsilon _i$
and
$\varepsilon _i$
and
![]() $\varepsilon _j$
. By assumption, the two integers
$\varepsilon _j$
. By assumption, the two integers
![]() $n_{ij}^{++}$
and
$n_{ij}^{++}$
and
![]() $n_{ij}^{-\,-}$
have the same parity. Since
$n_{ij}^{-\,-}$
have the same parity. Since
is even, the two integers
![]() $n_{ij}^{+-}$
and
$n_{ij}^{+-}$
and
![]() $n_{ij}^{-+}$
also have identical parity. Since
$n_{ij}^{-+}$
also have identical parity. Since
![]() $\ell (\varepsilon _i,\varepsilon _j)=\ell (-\varepsilon _i,-\varepsilon _j)$
, this leads to
$\ell (\varepsilon _i,\varepsilon _j)=\ell (-\varepsilon _i,-\varepsilon _j)$
, this leads to
This also leads to
and thus to the identity
![]() $B^E_{F'}=B^E_{F}\oplus (0)$
. The equality
$B^E_{F'}=B^E_{F}\oplus (0)$
. The equality
![]() $\mathit{Arf}(q^E_{F'})=\mathit{Arf}(q^E_{F})$
follows.
$\mathit{Arf}(q^E_{F'})=\mathit{Arf}(q^E_{F})$
follows.
The following lemma shows that we can partition the colors in two sets, inside of which changing crossings will not affect the Arf invariant.
Lemma 4.4. Let
![]() $E\subset \{\pm \}^m$
be of even cardinality. Then there exists a partition
$E\subset \{\pm \}^m$
be of even cardinality. Then there exists a partition
![]() $I_0\sqcup I_1$
of
$I_0\sqcup I_1$
of
![]() $\{1,\ldots , m\}$
such that for any
$\{1,\ldots , m\}$
such that for any
![]() $m$
-colored link
$m$
-colored link
![]() $L$
, the value of
$L$
, the value of
![]() $\mathit{Arf}_{\!E}(L)$
is invariant under crossing changes between components of colors belonging to the same subset of this partition.
$\mathit{Arf}_{\!E}(L)$
is invariant under crossing changes between components of colors belonging to the same subset of this partition.
Proof. Fix an arbitrary color
![]() $i\in \{1,\ldots ,m\}$
. For
$i\in \{1,\ldots ,m\}$
. For
![]() $s=0,1$
, set
$s=0,1$
, set
This obviously defines a partition
![]() $I_0\sqcup I_1$
of
$I_0\sqcup I_1$
of
![]() $\{1,\ldots ,m\}$
, with
$\{1,\ldots ,m\}$
, with
![]() $i\in I_0$
. By Lemma 4.2 and Lemma 4.3, it only remains to check that for any
$i\in I_0$
. By Lemma 4.2 and Lemma 4.3, it only remains to check that for any
![]() $j,k$
in the same subset of this partition, the integers
$j,k$
in the same subset of this partition, the integers
![]() $n_{jk}^{++}$
and
$n_{jk}^{++}$
and
![]() $n_{jk}^{-\,-}$
have the same parity. To show this claim, let us first denote by
$n_{jk}^{-\,-}$
have the same parity. To show this claim, let us first denote by
![]() $n_{ijk}^{\sigma \tau \eta }$
the cardinality of
$n_{ijk}^{\sigma \tau \eta }$
the cardinality of
![]() $\{\varepsilon \in E\,|\,\varepsilon _i=\sigma , \varepsilon _j=\tau , \varepsilon _k=\eta \}$
. Using the identity
$\{\varepsilon \in E\,|\,\varepsilon _i=\sigma , \varepsilon _j=\tau , \varepsilon _k=\eta \}$
. Using the identity
![]() $n_{ijk}^{+\sigma \tau }+n_{ijk}^{-\sigma \tau }=n_{jk}^{\sigma \tau }$
and variations thereof, together with the fact that
$n_{ijk}^{+\sigma \tau }+n_{ijk}^{-\sigma \tau }=n_{jk}^{\sigma \tau }$
and variations thereof, together with the fact that
![]() $\vert E\vert$
is even, we obtain the following equalities modulo 2:
$\vert E\vert$
is even, we obtain the following equalities modulo 2:
Since
![]() $j$
and
$j$
and
![]() $k$
belong to the same subset of the partition, this number is even, proving the claim.
$k$
belong to the same subset of the partition, this number is even, proving the claim.
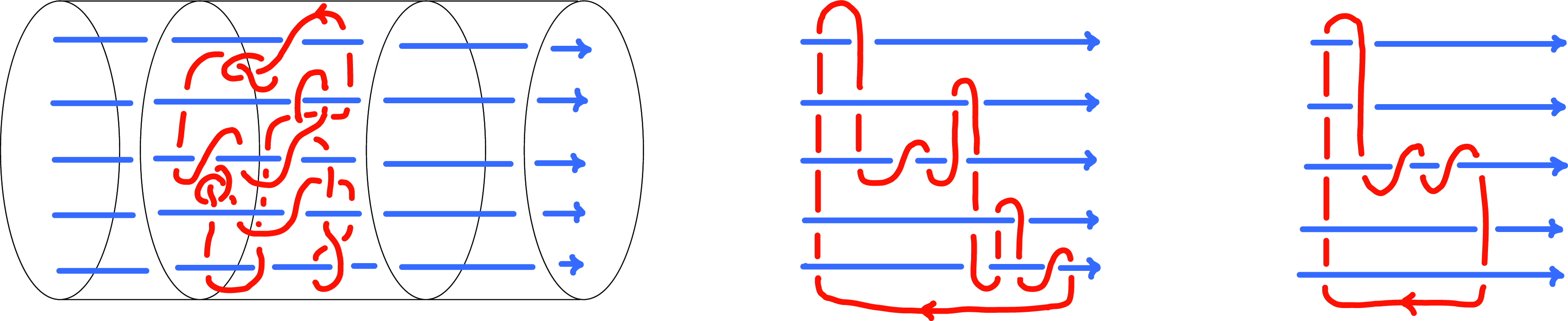
Figure 12. The three steps in obtaining the normal form.
The final lemma, which was communicated to us by Christopher Davis, states that
![]() $2$
-colored links are classified up to homotopy by the linking numbers of their components of different colors. More precisely, let us consider a
$2$
-colored links are classified up to homotopy by the linking numbers of their components of different colors. More precisely, let us consider a
![]() $2$
-colored link
$2$
-colored link
![]() $L=L_1\cup L_2$
. Given any ordering of the components of
$L=L_1\cup L_2$
. Given any ordering of the components of
![]() $L_1$
and any ordering of the components of
$L_1$
and any ordering of the components of
![]() $L_2$
, there is an associated matrix
$L_2$
, there is an associated matrix
![]() $\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
. This matrix is not canonically associated to
$\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
. This matrix is not canonically associated to
![]() $L$
, but any two such matrices for
$L$
, but any two such matrices for
![]() $L$
coincide up to reordering the rows and columns.
$L$
coincide up to reordering the rows and columns.
Lemma 4.5. Two 2-colored links
![]() $L=L_1\cup L_2$
and
$L=L_1\cup L_2$
and
![]() $L'=L_1'\cup L_2'$
are homotopic if and only if the associated matrices
$L'=L_1'\cup L_2'$
are homotopic if and only if the associated matrices
![]() $\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
and
$\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
and
![]() $\left ({\ell k}(K'_1,K'_2)\right )_{K'_1\subset L'_1,K'_2\subset L'_2}$
coincide up to reordering the rows and columns.
$\left ({\ell k}(K'_1,K'_2)\right )_{K'_1\subset L'_1,K'_2\subset L'_2}$
coincide up to reordering the rows and columns.
Proof. The matrix
![]() $\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
, considered up to reordering the rows and columns, is obviously invariant under homotopy. It remains to prove that this matrix determines the homotopy class of a 2-colored link. To do so, let us fix a 2-colored link
$\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
, considered up to reordering the rows and columns, is obviously invariant under homotopy. It remains to prove that this matrix determines the homotopy class of a 2-colored link. To do so, let us fix a 2-colored link
![]() $L=L_1\cup L_2$
together with arbitrary orderings of the components of
$L=L_1\cup L_2$
together with arbitrary orderings of the components of
![]() $L_1$
and of the components of
$L_1$
and of the components of
![]() $L_2$
. We will show that
$L_2$
. We will show that
![]() $L$
is homotopic to a link in a normal form which is uniquely determined up to isotopy by the corresponding matrix
$L$
is homotopic to a link in a normal form which is uniquely determined up to isotopy by the corresponding matrix
![]() $\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
.
$\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
.
Using homotopy between strands of color 1 (blue), one can first turn
![]() $L_1$
into the trivial link. To make it more concrete, let us say that
$L_1$
into the trivial link. To make it more concrete, let us say that
![]() $L_1$
is the closure of the trivial oriented braid in the cylinder
$L_1$
is the closure of the trivial oriented braid in the cylinder
![]() $D^2\times [0,1]$
, which we picture horizontally with the braid oriented left to right. Up to isotopy, the components of
$D^2\times [0,1]$
, which we picture horizontally with the braid oriented left to right. Up to isotopy, the components of
![]() $L_1$
can be permuted arbitrarily, so we can assume that their ordering (say, top to bottom) coincides with the fixed ordering. As a second step, we can now use homotopy between strands of color 2 (red) so that each of the components of
$L_1$
can be permuted arbitrarily, so we can assume that their ordering (say, top to bottom) coincides with the fixed ordering. As a second step, we can now use homotopy between strands of color 2 (red) so that each of the components of
![]() $L_2$
lies within a different slice of the cylinder, as illustrated in Figure 12 (left). Using homotopy, the components of
$L_2$
lies within a different slice of the cylinder, as illustrated in Figure 12 (left). Using homotopy, the components of
![]() $L_2$
can be permuted so that their ordering (left to right) coincides with the fixed ordering.
$L_2$
can be permuted so that their ordering (left to right) coincides with the fixed ordering.
It now remains to put any fixed component
![]() $K_2$
of
$K_2$
of
![]() $L_2$
in a normal form (within the corresponding cylinder slice) determined by the linking numbers
$L_2$
in a normal form (within the corresponding cylinder slice) determined by the linking numbers
![]() $\{{\ell k}(K_1,K_2)\}_{K_1\subset L_1}$
. To do so, first use homotopy within
$\{{\ell k}(K_1,K_2)\}_{K_1\subset L_1}$
. To do so, first use homotopy within
![]() $K_2$
to unknot it, and to put it in an “increasing” form inside its cylinder slice as illustrated in Figure 12 (center). Finally, consider the transformation illustrated below, which can be realized via a homotopy between components of color 1.
$K_2$
to unknot it, and to put it in an “increasing” form inside its cylinder slice as illustrated in Figure 12 (center). Finally, consider the transformation illustrated below, which can be realized via a homotopy between components of color 1.
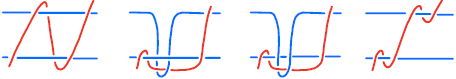
Using this movement, one can exchange the positions of two consecutive crossings between
![]() $K_2$
and
$K_2$
and
![]() $L_1$
. Since elementary transpositions generate all permutations, the crossings of
$L_1$
. Since elementary transpositions generate all permutations, the crossings of
![]() $K_1$
with
$K_1$
with
![]() $L_2$
can be permutated arbitrarily. Thus, we can order these crossings according to our fixed ordering of the components of
$L_2$
can be permutated arbitrarily. Thus, we can order these crossings according to our fixed ordering of the components of
![]() $L_1$
, leading to the final normal form illustrated in Figure 12 (right). This normal form being uniquely determined up to isotopy by the matrix
$L_1$
, leading to the final normal form illustrated in Figure 12 (right). This normal form being uniquely determined up to isotopy by the matrix
![]() $\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
, this concludes the proof.
$\left ({\ell k}(K_1,K_2)\right )_{K_1\subset L_1,K_2\subset L_2}$
, this concludes the proof.
Proof of Proposition 4.1
. Let us fix an
![]() $m$
-colored link
$m$
-colored link
![]() $L$
and some subset
$L$
and some subset
![]() $E\subset \{\pm \}^m$
of even cardinality. By Lemma 4.4, there exists a partition
$E\subset \{\pm \}^m$
of even cardinality. By Lemma 4.4, there exists a partition
![]() $\{1,\ldots , m\}=I_0\sqcup I_1$
such that
$\{1,\ldots , m\}=I_0\sqcup I_1$
such that
![]() $\mathit{Arf}_{\!E}(L')$
is invariant under crossing changes between components of colors belonging to the same subset. If one of the subsets
$\mathit{Arf}_{\!E}(L')$
is invariant under crossing changes between components of colors belonging to the same subset. If one of the subsets
![]() $I_0$
or
$I_0$
or
![]() $I_1$
is empty, then
$I_1$
is empty, then
![]() $\mathit{Arf}_{\!E}(L)$
does not depend on
$\mathit{Arf}_{\!E}(L)$
does not depend on
![]() $L$
and the proposition holds trivially. Otherwise, consider the 2-colored link
$L$
and the proposition holds trivially. Otherwise, consider the 2-colored link
![]() $\widetilde {L}$
obtained from
$\widetilde {L}$
obtained from
![]() $L$
by identifying the colors belonging to the same subset of the partition. We now know that the value of
$L$
by identifying the colors belonging to the same subset of the partition. We now know that the value of
![]() $\mathit{Arf}_{\!E}(L)$
is invariant under homotopy of the 2-colored link
$\mathit{Arf}_{\!E}(L)$
is invariant under homotopy of the 2-colored link
![]() $\widetilde {L}$
. By Lemma 4.5, the homotopy class of such a 2-colored link is determined by the linking numbers of its components. Since the linking numbers of the components of
$\widetilde {L}$
. By Lemma 4.5, the homotopy class of such a 2-colored link is determined by the linking numbers of its components. Since the linking numbers of the components of
![]() $L$
and of
$L$
and of
![]() $\widetilde {L}$
coincide, this concludes the proof.
$\widetilde {L}$
coincide, this concludes the proof.
Acknowledgments
The authors thank Anthony Conway and Stefan Friedl for helpful remarks on an earlier version of this article, and Christopher Davis for suggesting Lemma 4.5. Support from the Swiss NSF grant 200021-212085 is thankfully acknowledged.
Appendix A. Generalized S-equivalence for totally connected C-complexes
Consider two totally connected C-complexes for two isotopic colored links. The aim of this appendix is to give a detailed description of how the two sets of corresponding generalized Seifert matrices are related. (See [Reference Cimasoni4, Reference Davis, Martin and Otto13] for similar computations involving C-complexes that are not necessarily totally connected.)
We start with the proof of Lemma 2.5, whose statement we recall for the reader’s convenience.
Lemma A.1. Let
![]() $F$
and
$F$
and
![]() $F'$
be two totally connected C-complexes for isotopic colored links. Then, there exist totally connected C-complexes
$F'$
be two totally connected C-complexes for isotopic colored links. Then, there exist totally connected C-complexes
![]() $F=F^1,F^2,\ldots ,F^{n-1},F^n=F'$
such that for all
$F=F^1,F^2,\ldots ,F^{n-1},F^n=F'$
such that for all
![]() $1\le k \lt n$
,
$1\le k \lt n$
,
![]() $F^{k+1}$
is obtained from
$F^{k+1}$
is obtained from
![]() $F^k$
by one of the following moves or its inverse:
$F^k$
by one of the following moves or its inverse:
Proof. Let
![]() $F=F_1\cup \ldots \cup F_m$
and
$F=F_1\cup \ldots \cup F_m$
and
![]() $F'=F'_1\cup \ldots \cup F'_m$
be two totally connected C-complexes for isotopic colored links. By Lemma 4.2 of [Reference Davis, Martin and Otto13], there exists a C-complex
$F'=F'_1\cup \ldots \cup F'_m$
be two totally connected C-complexes for isotopic colored links. By Lemma 4.2 of [Reference Davis, Martin and Otto13], there exists a C-complex
![]() $G=G_1\cup \ldots \cup G_m$
(resp.
$G=G_1\cup \ldots \cup G_m$
(resp.
![]() $G'=G'_1\cup \ldots \cup G'_m$
) obtained from
$G'=G'_1\cup \ldots \cup G'_m$
) obtained from
![]() $F$
(resp.
$F$
(resp.
![]() $F'$
) by a sequence of isotopies and handle attachments, such that
$F'$
) by a sequence of isotopies and handle attachments, such that
![]() $G_i$
is isotopic to
$G_i$
is isotopic to
![]() $G_i'$
for all
$G_i'$
for all
![]() $i$
. Since the C-complexes
$i$
. Since the C-complexes
![]() $F$
and
$F$
and
![]() $F'$
are assumed to be totally connected with connected surfaces, so are all the C-complexes in these two sequences. Therefore, it can be assumed that
$F'$
are assumed to be totally connected with connected surfaces, so are all the C-complexes in these two sequences. Therefore, it can be assumed that
![]() $F$
and
$F$
and
![]() $F'$
are (totally connected) C-complexes with
$F'$
are (totally connected) C-complexes with
![]() $F_i$
and
$F_i$
and
![]() $F'_i$
connected and isotopic for all
$F'_i$
connected and isotopic for all
![]() $i$
. Propositions 4.3 and 4.6 of [Reference Davis, Martin and Otto13] then imply that there exists a sequence of C-complexes
$i$
. Propositions 4.3 and 4.6 of [Reference Davis, Martin and Otto13] then imply that there exists a sequence of C-complexes
![]() $F=F^1,F^2, \ldots ,F^{2\ell }=F'$
such that for all
$F=F^1,F^2, \ldots ,F^{2\ell }=F'$
such that for all
![]() $1\le k\lt \ell$
, the C-complex
$1\le k\lt \ell$
, the C-complex
![]() $F^{2k}$
is obtained from
$F^{2k}$
is obtained from
![]() $F^{2k-1}$
by an ambient isotopy while
$F^{2k-1}$
by an ambient isotopy while
![]() $F^{2k+1}$
is obtained from
$F^{2k+1}$
is obtained from
![]() $F^{2k}$
by a move (T2), (T3), (T4), or its inverse. The possible issue here is that the inverse of a move (T2) or a move (T3) might transform a totally connected C-complex into a no longer totally connected one. However, the following procedure ensures that such a move can be replaced by other ones that keep the C-complexes totally connected.
$F^{2k}$
by a move (T2), (T3), (T4), or its inverse. The possible issue here is that the inverse of a move (T2) or a move (T3) might transform a totally connected C-complex into a no longer totally connected one. However, the following procedure ensures that such a move can be replaced by other ones that keep the C-complexes totally connected.
To describe it, we first fix some terminology and notation. For all
![]() $1\le k\lt \ell$
, let us denote by
$1\le k\lt \ell$
, let us denote by
![]() $\mathrm{T}_k$
the move performed on
$\mathrm{T}_k$
the move performed on
![]() $F^{2k}$
to obtain
$F^{2k}$
to obtain
![]() $F^{2k+1}$
, and by
$F^{2k+1}$
, and by
![]() $B_k$
a (small)
$B_k$
a (small)
![]() $3$
-ball containing the support of this move. Fixing
$3$
-ball containing the support of this move. Fixing
![]() $1\le i\neq j\le m$
, we shall say that a C-complex is
$1\le i\neq j\le m$
, we shall say that a C-complex is
![]() $(i,j)$
-connected if its surfaces of colors
$(i,j)$
-connected if its surfaces of colors
![]() $i$
and
$i$
and
![]() $j$
intersect. If all the C-complexes
$j$
intersect. If all the C-complexes
![]() $F^1,F^2, \ldots ,F^{2\ell }$
are
$F^1,F^2, \ldots ,F^{2\ell }$
are
![]() $(i,j)$
-connected, then there is nothing to do. Otherwise, let
$(i,j)$
-connected, then there is nothing to do. Otherwise, let
![]() $\kappa \in \{1,\ldots ,\ell -1\}$
denote the first time when
$\kappa \in \{1,\ldots ,\ell -1\}$
denote the first time when
![]() $(i,j)$
-connectivity is lost; in other words, let us suppose that
$(i,j)$
-connectivity is lost; in other words, let us suppose that
![]() $F^{2k-1}\simeq F^{2k}$
is
$F^{2k-1}\simeq F^{2k}$
is
![]() $(i,j)$
-connected for
$(i,j)$
-connected for
![]() $1\le k\le \kappa$
, but that
$1\le k\le \kappa$
, but that
![]() $F^{2\kappa +1}_i \cap F^{2\kappa +1}_j$
is empty. Then, fix a simple arc
$F^{2\kappa +1}_i \cap F^{2\kappa +1}_j$
is empty. Then, fix a simple arc
![]() $\gamma _\kappa$
linking a point of
$\gamma _\kappa$
linking a point of
![]() $\partial F^{2\kappa }_i \backslash B_{\kappa }$
and a point of
$\partial F^{2\kappa }_i \backslash B_{\kappa }$
and a point of
![]() $\partial F^{2\kappa }_j \backslash B_{\kappa }$
, with the interior of
$\partial F^{2\kappa }_j \backslash B_{\kappa }$
, with the interior of
![]() $\gamma _\kappa$
disjoint from
$\gamma _\kappa$
disjoint from
![]() $F^{2\kappa }\cup B_{\kappa }$
. As illustrated in Figure A.1, perform a “connection” via a move (T2) along
$F^{2\kappa }\cup B_{\kappa }$
. As illustrated in Figure A.1, perform a “connection” via a move (T2) along
![]() $\gamma _\kappa$
, a transformation whose support lies in a small tubular neihbourhood
$\gamma _\kappa$
, a transformation whose support lies in a small tubular neihbourhood
![]() $\Gamma _\kappa$
of
$\Gamma _\kappa$
of
![]() $\gamma _\kappa$
. Performing the move (T
$\gamma _\kappa$
. Performing the move (T
![]() $_\kappa$
) on the result produces an
$_\kappa$
) on the result produces an
![]() $(i,j)$
-connected C-complex
$(i,j)$
-connected C-complex
![]() $(F^{2\kappa +1})'$
, and applying the ambient isotopy
$(F^{2\kappa +1})'$
, and applying the ambient isotopy
![]() $F^{2\kappa +1}\simeq F^{2\kappa +2}$
to
$F^{2\kappa +1}\simeq F^{2\kappa +2}$
to
![]() $(F^{2\kappa +1})'$
yields a C-complex
$(F^{2\kappa +1})'$
yields a C-complex
![]() $(F^{2\kappa +2})'$
, which is obviously
$(F^{2\kappa +2})'$
, which is obviously
![]() $(i,j)$
-connected as well. Since the image of
$(i,j)$
-connected as well. Since the image of
![]() $\Gamma _\kappa$
by the previous isotopy might intersect
$\Gamma _\kappa$
by the previous isotopy might intersect
![]() $B_{\kappa +1}$
, let us now first perform a new connection along an arc
$B_{\kappa +1}$
, let us now first perform a new connection along an arc
![]() $\gamma _{\kappa +1}$
linking a point of
$\gamma _{\kappa +1}$
linking a point of
![]() $(F^{2\kappa +2})'_i \backslash B_{\kappa +1}$
with a point of
$(F^{2\kappa +2})'_i \backslash B_{\kappa +1}$
with a point of
![]() $(F^{2\kappa +2})'_j \backslash B_{\kappa +1}$
, with the interior of
$(F^{2\kappa +2})'_j \backslash B_{\kappa +1}$
, with the interior of
![]() $\gamma _{\kappa +1}$
disjoint from
$\gamma _{\kappa +1}$
disjoint from
![]() $(F^{2\kappa +2})' \cup B_{\kappa +1}$
. Then, remove the first connection (via the inverse of a move (T2) and an isotopy) and finally perform the move (
$(F^{2\kappa +2})' \cup B_{\kappa +1}$
. Then, remove the first connection (via the inverse of a move (T2) and an isotopy) and finally perform the move (
![]() $\mathrm{T}_{\kappa +1}$
) on the result, yielding an
$\mathrm{T}_{\kappa +1}$
) on the result, yielding an
![]() $(i,j)$
-connected C-complex
$(i,j)$
-connected C-complex
![]() $(F^{2\kappa +3})'$
. Iterating this procedure produces a sequence of
$(F^{2\kappa +3})'$
. Iterating this procedure produces a sequence of
![]() $(i,j)$
-connected C-complexes from
$(i,j)$
-connected C-complexes from
![]() $F$
to a C-complex obtained from
$F$
to a C-complex obtained from
![]() $F'$
by a move (T2) involving the surfaces
$F'$
by a move (T2) involving the surfaces
![]() $F_i'$
and
$F_i'$
and
![]() $F_j'$
. This connection can be removed, resulting in a sequence of
$F_j'$
. This connection can be removed, resulting in a sequence of
![]() $(i,j)$
-connected C-complexes from
$(i,j)$
-connected C-complexes from
![]() $F$
to
$F$
to
![]() $F'$
. Applying this to all pairs of colors yields the desired result.
$F'$
. Applying this to all pairs of colors yields the desired result.
We now exhibit how moves (T1) to (T4) affect the corresponding generalized Seifert matrices. The result is a extended notion of S-equivalence valid for generalized Seifert matrices associated to totally connected C-complexes. This requires some notation.
Notation A.2. Given two signs
![]() $\varepsilon ,\sigma \in \{\pm \}$
, we write
$\varepsilon ,\sigma \in \{\pm \}$
, we write
![]() $\delta (\varepsilon ,\sigma )=1$
if
$\delta (\varepsilon ,\sigma )=1$
if
![]() $\varepsilon =\sigma$
, and
$\varepsilon =\sigma$
, and
![]() $\delta (\varepsilon ,\sigma )=0$
otherwise. Also, for
$\delta (\varepsilon ,\sigma )=0$
otherwise. Also, for
![]() $z$
an element of a basis of a free abelian group
$z$
an element of a basis of a free abelian group
![]() $H\simeq \mathbb{Z}^d$
, we let
$H\simeq \mathbb{Z}^d$
, we let
![]() $\chi (z)$
denote the element in
$\chi (z)$
denote the element in
![]() $\mathbb{Z}^d$
with the
$\mathbb{Z}^d$
with the
![]() $z$
-coordinate equal to
$z$
-coordinate equal to
![]() $1$
and all the others equal to
$1$
and all the others equal to
![]() $0$
.
$0$
.
(T1) Let
![]() $F'$
be a C-complex obtained from a C-complex
$F'$
be a C-complex obtained from a C-complex
![]() $F$
by a movement (T1) on the
$F$
by a movement (T1) on the
![]() $\sigma _i$
-side of
$\sigma _i$
-side of
![]() $F_i$
, for some fixed color
$F_i$
, for some fixed color
![]() $i\in \{1,\ldots ,m\}$
and sign
$i\in \{1,\ldots ,m\}$
and sign
![]() $\sigma _i=\pm$
. Since
$\sigma _i=\pm$
. Since
![]() $F_i$
is connected, we have
$F_i$
is connected, we have
![]() $H_1(F')=H_1(F)\oplus \mathbb{Z}x' \oplus \mathbb{Z}y'$
, with
$H_1(F')=H_1(F)\oplus \mathbb{Z}x' \oplus \mathbb{Z}y'$
, with
![]() $x'$
and
$x'$
and
![]() $y'$
the cycles represented in the top part of Figure 2. In the corresponding basis of
$y'$
the cycles represented in the top part of Figure 2. In the corresponding basis of
![]() $H_1(F')$
, the generalized Seifert matrix
$H_1(F')$
, the generalized Seifert matrix
![]() $A^\varepsilon _{F'}$
is obtained from
$A^\varepsilon _{F'}$
is obtained from
![]() $A^\varepsilon _F$
via
$A^\varepsilon _F$
via
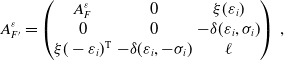 \begin{equation} A^\varepsilon _{F'}=\begin{pmatrix} A^\varepsilon _F & 0 & \xi (\varepsilon _i) \\ 0 & 0 & -\delta (\varepsilon _i,\sigma _i) \\ \xi (-\varepsilon _i)^{{\operatorname {T}}} & -\delta (\varepsilon _i,-\sigma _i) & \ell \end{pmatrix}\,, \end{equation}
\begin{equation} A^\varepsilon _{F'}=\begin{pmatrix} A^\varepsilon _F & 0 & \xi (\varepsilon _i) \\ 0 & 0 & -\delta (\varepsilon _i,\sigma _i) \\ \xi (-\varepsilon _i)^{{\operatorname {T}}} & -\delta (\varepsilon _i,-\sigma _i) & \ell \end{pmatrix}\,, \end{equation}
with
![]() $\ell \in \mathbb{Z}$
and
$\ell \in \mathbb{Z}$
and
![]() $\xi (\varepsilon _i)$
some integral vector.
$\xi (\varepsilon _i)$
some integral vector.
(T2) Let us now fix two colors
![]() $i,j\in \{1,\ldots ,m\}$
and two signs
$i,j\in \{1,\ldots ,m\}$
and two signs
![]() $\sigma _i, \sigma _j$
. Let
$\sigma _i, \sigma _j$
. Let
![]() $F'$
be the (totally connected) C-complex obtained from a totally connected C-complex
$F'$
be the (totally connected) C-complex obtained from a totally connected C-complex
![]() $F$
by a movement (T2) between the surfaces
$F$
by a movement (T2) between the surfaces
![]() $F_i$
and
$F_i$
and
![]() $F_j$
, as illustrated in the bottom part of Figure 2. Since
$F_j$
, as illustrated in the bottom part of Figure 2. Since
![]() $F$
is totally connected, we have
$F$
is totally connected, we have
![]() $H_1(F')=H_1(F)\oplus \mathbb{Z}x' \oplus \mathbb{Z}y'$
, with
$H_1(F')=H_1(F)\oplus \mathbb{Z}x' \oplus \mathbb{Z}y'$
, with
![]() $x',y'\subset F'_i\cup F'_j$
the cycles represented in Figure 2. In the corresponding basis of
$x',y'\subset F'_i\cup F'_j$
the cycles represented in Figure 2. In the corresponding basis of
![]() $H_1(F')$
, the generalized Seifert matrix
$H_1(F')$
, the generalized Seifert matrix
![]() $A^\varepsilon _{F'}$
is obtained from
$A^\varepsilon _{F'}$
is obtained from
![]() $A^\varepsilon _F$
via
$A^\varepsilon _F$
via
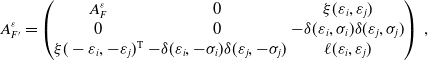 \begin{equation*} A^\varepsilon _{F'}=\begin{pmatrix} A^\varepsilon _F & 0 & \xi (\varepsilon _i,\varepsilon _j)\\ 0 & 0 & -\delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}} & -\delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i,\varepsilon _j) \end{pmatrix}\,, \end{equation*}
\begin{equation*} A^\varepsilon _{F'}=\begin{pmatrix} A^\varepsilon _F & 0 & \xi (\varepsilon _i,\varepsilon _j)\\ 0 & 0 & -\delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}} & -\delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i,\varepsilon _j) \end{pmatrix}\,, \end{equation*}
with
![]() $\ell (\varepsilon _i,\varepsilon _j)=\ell (-\varepsilon _i,-\varepsilon _j)\in \mathbb{Z}$
and
$\ell (\varepsilon _i,\varepsilon _j)=\ell (-\varepsilon _i,-\varepsilon _j)\in \mathbb{Z}$
and
![]() $\xi (\varepsilon _i,\varepsilon _j)$
some integral vector which only depends on
$\xi (\varepsilon _i,\varepsilon _j)$
some integral vector which only depends on
![]() $\varepsilon _i$
and
$\varepsilon _i$
and
![]() $\varepsilon _j$
.
$\varepsilon _j$
.
(T3) Fix three colors
![]() $i,j,k\in \{1,\ldots ,m\}$
and three signs
$i,j,k\in \{1,\ldots ,m\}$
and three signs
![]() $\sigma _i, \sigma _j, \sigma _k$
. Let
$\sigma _i, \sigma _j, \sigma _k$
. Let
![]() $F'$
be the totally connected C-complex obtained from the totally connected C-complex
$F'$
be the totally connected C-complex obtained from the totally connected C-complex
![]() $F$
by a movement (T3) between the surfaces
$F$
by a movement (T3) between the surfaces
![]() $F_i$
,
$F_i$
,
![]() $F_j$
and
$F_j$
and
![]() $F_k$
as illustrated in Figure 8. The homology groups
$F_k$
as illustrated in Figure 8. The homology groups
![]() $H_1(F)$
and
$H_1(F)$
and
![]() $H_1(F')$
are naturally isomorphic, with the cycle
$H_1(F')$
are naturally isomorphic, with the cycle
![]() $x$
in
$x$
in
![]() $F$
mapped to the cycle
$F$
mapped to the cycle
![]() $x'$
in
$x'$
in
![]() $F'$
, see Figure 8. The total connectivity of
$F'$
, see Figure 8. The total connectivity of
![]() $F$
(resp.
$F$
(resp.
![]() $F'$
) guarantees the existence of a cycle
$F'$
) guarantees the existence of a cycle
![]() $y\subset F_i\cup F_k$
(resp.
$y\subset F_i\cup F_k$
(resp.
![]() $y'\subset F'_i\cup F'_j\cup F'_k$
) as illustrated in Figure 8, with the natural isomorphism
$y'\subset F'_i\cup F'_j\cup F'_k$
) as illustrated in Figure 8, with the natural isomorphism
![]() $H_1(F)\simeq H_1(F')$
mapping
$H_1(F)\simeq H_1(F')$
mapping
![]() $y$
to
$y$
to
![]() $y'$
. For the same reason, there exist cycles
$y'$
. For the same reason, there exist cycles
![]() $z\subset F$
and
$z\subset F$
and
![]() $z'\subset F'$
as depicted in Figure 8; moreover, one can fix a basis of
$z'\subset F'$
as depicted in Figure 8; moreover, one can fix a basis of
![]() $H_1(F)$
(resp.
$H_1(F)$
(resp.
![]() $H_1(F')$
) having a unique cycle
$H_1(F')$
) having a unique cycle
![]() $z$
(resp.
$z$
(resp.
![]() $z'$
) of this form. With respect to a basis of
$z'$
) of this form. With respect to a basis of
![]() $H_1(F)$
(resp.
$H_1(F)$
(resp.
![]() $H_1(F')$
) having
$H_1(F')$
) having
![]() $x,y$
(resp.
$x,y$
(resp.
![]() $x',y'$
) as last two elements, the generalized Seifert matrices then have the form
$x',y'$
) as last two elements, the generalized Seifert matrices then have the form
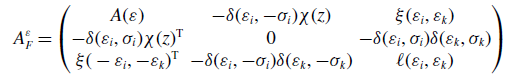 \begin{equation*} A^\varepsilon _{F}=\begin{pmatrix} A(\varepsilon ) & -\delta (\varepsilon _i,-\sigma _i)\chi (z) & \xi (\varepsilon _i,\varepsilon _k)\\ -\delta (\varepsilon _i,\sigma _i)\chi (z)^{{\operatorname {T}}} & 0 & -\delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _k,\sigma _k)\\ \xi (-\varepsilon _i,-\varepsilon _k)^{{\operatorname {T}}} & -\delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _k,-\sigma _k) & \ell (\varepsilon _i,\varepsilon _k) \end{pmatrix} \end{equation*}
\begin{equation*} A^\varepsilon _{F}=\begin{pmatrix} A(\varepsilon ) & -\delta (\varepsilon _i,-\sigma _i)\chi (z) & \xi (\varepsilon _i,\varepsilon _k)\\ -\delta (\varepsilon _i,\sigma _i)\chi (z)^{{\operatorname {T}}} & 0 & -\delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _k,\sigma _k)\\ \xi (-\varepsilon _i,-\varepsilon _k)^{{\operatorname {T}}} & -\delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _k,-\sigma _k) & \ell (\varepsilon _i,\varepsilon _k) \end{pmatrix} \end{equation*}
and
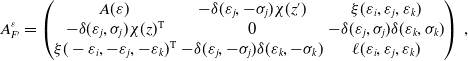 \begin{equation*} A^\varepsilon _{F'}=\begin{pmatrix} A(\varepsilon ) & -\delta (\varepsilon _j,-\sigma _j)\chi (z') & \xi (\varepsilon _i,\varepsilon _j, \varepsilon _k)\\ -\delta (\varepsilon _j,\sigma _j)\chi (z)^{{\operatorname {T}}} & 0 & -\delta (\varepsilon _j,\sigma _j)\delta (\varepsilon _k,\sigma _k)\\ \xi (-\varepsilon _i,-\varepsilon _j,-\varepsilon _k)^{{\operatorname {T}}} & -\delta (\varepsilon _j,-\sigma _j)\delta (\varepsilon _k,-\sigma _k) & \ell (\varepsilon _i, \varepsilon _j, \varepsilon _k) \end{pmatrix}\,, \end{equation*}
\begin{equation*} A^\varepsilon _{F'}=\begin{pmatrix} A(\varepsilon ) & -\delta (\varepsilon _j,-\sigma _j)\chi (z') & \xi (\varepsilon _i,\varepsilon _j, \varepsilon _k)\\ -\delta (\varepsilon _j,\sigma _j)\chi (z)^{{\operatorname {T}}} & 0 & -\delta (\varepsilon _j,\sigma _j)\delta (\varepsilon _k,\sigma _k)\\ \xi (-\varepsilon _i,-\varepsilon _j,-\varepsilon _k)^{{\operatorname {T}}} & -\delta (\varepsilon _j,-\sigma _j)\delta (\varepsilon _k,-\sigma _k) & \ell (\varepsilon _i, \varepsilon _j, \varepsilon _k) \end{pmatrix}\,, \end{equation*}
with
![]() $\ell (\varepsilon _i, \varepsilon _j, \varepsilon _k)\in \mathbb{Z}$
,
$\ell (\varepsilon _i, \varepsilon _j, \varepsilon _k)\in \mathbb{Z}$
,
![]() $\xi (\varepsilon _i, \varepsilon _j, \varepsilon _k)$
an integral vector and
$\xi (\varepsilon _i, \varepsilon _j, \varepsilon _k)$
an integral vector and
![]() $A(\varepsilon )$
an integral matrix.
$A(\varepsilon )$
an integral matrix.
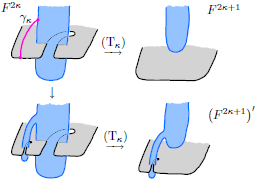
Figure A.1. A connection via a move (T2) along an arc.
(T4) Finally, fix two colors
![]() $i,j\in \{1,\ldots ,m\}$
and two signs
$i,j\in \{1,\ldots ,m\}$
and two signs
![]() $\sigma _i, \sigma _j$
. Let
$\sigma _i, \sigma _j$
. Let
![]() $F'$
be the C-complex obtained from a C-complex
$F'$
be the C-complex obtained from a C-complex
![]() $F$
by a movement (T4) between the surfaces
$F$
by a movement (T4) between the surfaces
![]() $F_i$
and
$F_i$
and
![]() $F_j$
as in Figure A.2. Via conjugation by a move (T2) along
$F_j$
as in Figure A.2. Via conjugation by a move (T2) along
![]() $F_i\cup F_j$
and by moves (T1) along
$F_i\cup F_j$
and by moves (T1) along
![]() $F_i$
and along
$F_i$
and along
![]() $F_j$
, one can fix a basis of
$F_j$
, one can fix a basis of
![]() $H_1(F)$
(resp.
$H_1(F)$
(resp.
![]() $H_1(F')$
) containing exactly three cycles
$H_1(F')$
) containing exactly three cycles
![]() $x,y,z\subset F_i\cup F_j$
(resp.
$x,y,z\subset F_i\cup F_j$
(resp.
![]() $x',y',z'\subset F'_i\cup F_j'$
) as in Figure A.2. There is a natural isomorphism
$x',y',z'\subset F'_i\cup F_j'$
) as in Figure A.2. There is a natural isomorphism
![]() $H_1(F)\simeq H_1(F')$
mapping the classes of
$H_1(F)\simeq H_1(F')$
mapping the classes of
![]() $x,y,z$
to the classes of
$x,y,z$
to the classes of
![]() $x',y',z'$
, respectively. Expressed in a basis of
$x',y',z'$
, respectively. Expressed in a basis of
![]() $H_1(F)$
(resp.
$H_1(F)$
(resp.
![]() $H_1(F')$
) as above and having
$H_1(F')$
) as above and having
![]() $x,y$
(resp.
$x,y$
(resp.
![]() $x',y'$
) as last two elements, and using the aforementioned isomorphism, the generalized Seifert matrices have the form
$x',y'$
) as last two elements, and using the aforementioned isomorphism, the generalized Seifert matrices have the form
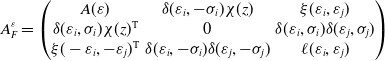 \begin{equation} A^\varepsilon _{F}=\begin{pmatrix} A(\varepsilon ) & \delta (\varepsilon _i,-\sigma _i)\chi (z) & \xi (\varepsilon _i,\varepsilon _j)\\ \delta (\varepsilon _i,\sigma _i)\chi (z)^{{\operatorname {T}}} & 0 & \delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}} & \delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i,\varepsilon _j) \end{pmatrix} \end{equation}
\begin{equation} A^\varepsilon _{F}=\begin{pmatrix} A(\varepsilon ) & \delta (\varepsilon _i,-\sigma _i)\chi (z) & \xi (\varepsilon _i,\varepsilon _j)\\ \delta (\varepsilon _i,\sigma _i)\chi (z)^{{\operatorname {T}}} & 0 & \delta (\varepsilon _i,\sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}} & \delta (\varepsilon _i,-\sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i,\varepsilon _j) \end{pmatrix} \end{equation}
and
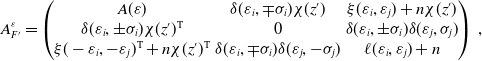 \begin{equation} A^\varepsilon _{F'}=\begin{pmatrix} A(\varepsilon ) & \delta (\varepsilon _i,\mp \sigma _i)\chi (z') & \xi (\varepsilon _i,\varepsilon _j)+n\chi (z')\\ \delta (\varepsilon _i,\pm \sigma _i)\chi (z')^{{\operatorname {T}}} & 0 & \delta (\varepsilon _i,\pm \sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}}+n\chi (z')^{{\operatorname {T}}} & \delta (\varepsilon _i,\mp \sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i, \varepsilon _j)+n \end{pmatrix}\,, \end{equation}
\begin{equation} A^\varepsilon _{F'}=\begin{pmatrix} A(\varepsilon ) & \delta (\varepsilon _i,\mp \sigma _i)\chi (z') & \xi (\varepsilon _i,\varepsilon _j)+n\chi (z')\\ \delta (\varepsilon _i,\pm \sigma _i)\chi (z')^{{\operatorname {T}}} & 0 & \delta (\varepsilon _i,\pm \sigma _i)\delta (\varepsilon _j,\sigma _j)\\ \xi (-\varepsilon _i,-\varepsilon _j)^{{\operatorname {T}}}+n\chi (z')^{{\operatorname {T}}} & \delta (\varepsilon _i,\mp \sigma _i)\delta (\varepsilon _j,-\sigma _j) & \ell (\varepsilon _i, \varepsilon _j)+n \end{pmatrix}\,, \end{equation}
with
![]() $\ell (\varepsilon _i, \varepsilon _j)\in \mathbb{Z}$
,
$\ell (\varepsilon _i, \varepsilon _j)\in \mathbb{Z}$
,
![]() $\xi (\varepsilon _i,\varepsilon _j)$
an integral vector,
$\xi (\varepsilon _i,\varepsilon _j)$
an integral vector,
![]() $A(\varepsilon )$
an integral matrix, and
$A(\varepsilon )$
an integral matrix, and
![]() $n\in \mathbb{Z}$
independent of
$n\in \mathbb{Z}$
independent of
![]() $\varepsilon$
. This integer is the winding number of the path around the ribbon; in particular, it vanishes in the case of
$\varepsilon$
. This integer is the winding number of the path around the ribbon; in particular, it vanishes in the case of
![]() $(\mathrm{T4_a})$
illustrated in the left of Figure 4. The sign in front of
$(\mathrm{T4_a})$
illustrated in the left of Figure 4. The sign in front of
![]() $\sigma _i$
depends on how the arc traverses
$\sigma _i$
depends on how the arc traverses
![]() $F_i$
, the two different cases being illustrated in Figure A.2.
$F_i$
, the two different cases being illustrated in Figure A.2.
Figure A.2. The surfaces and cycles involved in two possible versions of the move (T4).
In conclusion, two sets of generalized Seifert matrices corresponding to totally connected C-complexes for isotopic colored links are related by simultaneous congruences, and the four transformations described above.




























