Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:55:34.561Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CERTAIN APPLICATIONS OF THE KHUKHRO–MAKARENKO THEOREM

Published online by Cambridge University Press:  02 August 2012

AHMET ARIKAN ,
HOWARD SMITH  and
NADIR TRABELSI
AHMET ARIKAN
Affiliation:
Gazi Üniversitesi, Gazi Eǧitim Fakültesi, Matematik Eğitimi Anabilim Dalı 06500 Teknikokullar, Ankara, Turkey e-mail: arikan@gazi.edu.tr
HOWARD SMITH
Affiliation:
Department of Mathematics, Bucknell University, Lewisburg, PA 17837, USA e-mail: howsmith@bucknell.edu
NADIR TRABELSI
Affiliation:
Laboratory of Fundamental and Numerical Mathematics, Department of Mathematics, University Ferhat Abbas of Setif, Algeria e-mail: nadir_trabelsi@yahoo.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some recent results of Khukhro and Makarenko on the existence of characteristic 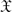-subgroups of finite index in a group G, for certain varieties 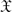, are used to obtain generalisations of some well-known results in the literature pertaining to groups G, in which all proper subgroups satisfy some condition or other related to the property ‘soluble-by-finite’. In addition, a partial generalisation is obtained for the aforementioned results on the existence of characteristic subgroups.

Keywords

20F1020F1920E50
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 2 , May 2013 , pp. 275 - 283
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Arıkan, A., On barely transitive p-groups with soluble point stabilizer, J. Group Theory 5 (2002), 441–442.CrossRefGoogle Scholar
2.Belyaev, V. V. and Kuzucuoglu, M., Locally finite barely transitive groups, Algebra Logic 42 (2003), 147–152 (translated from Algebra i Logika 42 (2003), 261–270).Google Scholar
3.Bruno, B. and Napolitani, F., A note on nilpotent-by-Cernikov groups, Glasgow. Math. J. 46 (2004), 211–215.CrossRefGoogle Scholar
4.Dixon, M. R., Evans, M. J. and Smith, H., Locally (soluble-by-finite) groups with all proper non-nilpotent subgroups of finite rank, J. Pure Appl. Algebra 135 (1999), 33–43.Google Scholar
5.Dixon, M. R., Evans, M. J. and Smith, H., Groups with all proper subgroups nilpotent-by-finite rank, Arch. Math. 75 (2000), 81–91.Google Scholar
6.Dixon, M. R., Evans, M. J. and Smith, H., Groups with all proper subgroups soluble-by-finite rank, J. of Algebra 289 (2005), 135–147.Google Scholar
7.Hartley, B., On the normalizer condition and barely transitive permutation groups, Algebra Logic 13 (1974), 334–340 (translated from Russian from Algebra i Logika 13 (1974), 589–602).Google Scholar
8.Hartley, B., Periodic locally soluble groups containing an element of prime order with Chernikov centralizer, Quart. J. Math. Oxford Ser. 42 (2) (1982), 309–323.Google Scholar
9.Khukhro, E. I. and Makarenko, N. Yu., Large characteristic subgroups satisfying multilinear commutator identities, J. Lond. Math. Soc. 75 (2) (2007), 635–646.CrossRefGoogle Scholar
10.Khukhro, E. I. and Makarenko, N. Yu., Automorphically invariant ideals satisfying multilinear identities, and group-theoretic applications, J. Algebra 320 (2008), 1723–1740.Google Scholar
11.Khukhro, E. I., Klyachko, A. A., Makarenko, N. Yu. and Mel'nikova, Yu. B., Automorphism invarience and identities, Bull. Lond. Math. Soc. 41 (2009), 804–816.CrossRefGoogle Scholar
12.Kleidman, P. B. and Wilson, R. A., A characterization of some locally finite simple groups of lie type, Arch. Mat. 48 (1987), 10–14.CrossRefGoogle Scholar
13.Klyachko, A. A. and Mel'nikova, Yu. B., A short proof of Makarenko–Khukhro Theorem on a large characteristic subgroups with identity, Sb. Math. 200 (2009), 661–664 (translated from Russian from Mat. Sb. 200 (2009), 33–36).CrossRefGoogle Scholar
14.Lennox, J. C. and Robinson, D. J. S., The theory of infinite soluble groups (Clarendon Press, Oxford, UK, 2004).Google Scholar
15.Lennox, J. C. and Stonehewer, S. E., Subnormal subgroups of groups, Oxford Mathematical Monographs (Clarendon Press, Oxford, UK, 1987).Google Scholar
16.Moghaddam, M. R. R., On the Schur–Baer property, J. Austral. Math. Soc. A 31 (1981), 343–361.CrossRefGoogle Scholar
17.Robinson, D. J. S., Finiteness conditions and generalized soluble groups, Part 2 (Springer-Verlag, New York, 1972).Google Scholar
18.Robinson, D. J. S., A course in the theory of groups (Springer-Verlag, New York, 1982).Google Scholar
19.Shumyatsky, P., Centralizers in locally finite groups, Turk. J. Math. 31 (2007), 149–170.Google Scholar