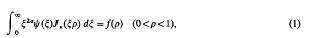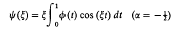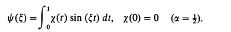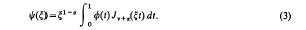Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sneddon, I. N.
1962.
Note on an electrified circular disk situated inside a coaxial infinite hollow cylinder.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 58,
Issue. 4,
p.
621.
Burlak, J.
1962.
A Pair of Dual Integral Equations Occurring in Diffraction Theory.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 2,
p.
179.
Erdélyi, A.
and
Sneddon, I. N.
1962.
Fractional Integration and Dual Integral Equations.
Canadian Journal of Mathematics,
Vol. 14,
Issue. ,
p.
685.
Burlak, J.
1963.
On the solution of certain dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 1,
p.
39.
Lowengrub, M.
and
Sneddon, I. N.
1963.
The solution of a pair of dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 1,
p.
14.
Williams, W. E.
1964.
The solution of dual series and dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 3,
p.
123.
Srivastav, R. P.
1964.
A Pair of Dual Integral Equations Involving Bessel Functions of the First and the Second Kind.
Proceedings of the Edinburgh Mathematical Society,
Vol. 14,
Issue. 2,
p.
149.
Burlak, J.
1964.
On Gordon's method of solving dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 3,
p.
117.
Erdogan, F.
and
Bahar, L. Y.
1964.
On the Solution of Simultaneous Dual Integral Equations.
Journal of the Society for Industrial and Applied Mathematics,
Vol. 12,
Issue. 3,
p.
666.
Westmann, R. A.
1965.
Simultaneous Pairs of Dual Integral Equations.
SIAM Review,
Vol. 7,
Issue. 3,
p.
341.
Keer, Leon M.
1965.
Nonaxisymmetric punch and crack problems for initially stressed bodies.
Quarterly of Applied Mathematics,
Vol. 23,
Issue. 2,
p.
97.
Brutsaert, Wilfried
1967.
Evaporation from a very small water surface at ground level: Three-dimensional turbulent diffusion without convection.
Journal of Geophysical Research,
Vol. 72,
Issue. 22,
p.
5631.
Kesarwani, Roop Narain
1967.
Fractional integration and certain dual integral equations.
Mathematische Zeitschrift,
Vol. 98,
Issue. 1,
p.
83.
Keer, L. M.
1968.
Coupled pairs of dual integral equations.
Quarterly of Applied Mathematics,
Vol. 25,
Issue. 4,
p.
453.
Erdogan, F. F.
1968.
Simultaneous dual integral equations with trigonometric and Bessel kernels.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 48,
Issue. 4,
p.
217.
Lowengrub, M.
1968.
The solution of certain simultaneous pairs of dual integral equations.
Glasgow Mathematical Journal,
Vol. 9,
Issue. 2,
p.
92.
Keer, L. M.
and
Freeman, N. J.
1969.
Torsion of a finite elastic cylindrical rod partially bonded to an elastic half space.
Quarterly of Applied Mathematics,
Vol. 26,
Issue. 4,
p.
567.
Brutsaert, Wilfried
and
Yeh, Gour-Tsyh
1969.
Evaporation from an extremely narrow wet strip at ground level.
Journal of Geophysical Research,
Vol. 74,
Issue. 13,
p.
3431.
Kassir, M. K.
1972.
A note on the twisting deformation of a non-homogeneous shaft containing a circular crack.
International Journal of Fracture Mechanics,
Vol. 8,
Issue. 3,
p.
325.
Sneddon, Ian Naismith
1975.
Fractional Calculus and Its Applications.
Vol. 457,
Issue. ,
p.
37.