Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T12:36:13.648Z Has data issue: false hasContentIssue false
  • English
  • Français

On dilation equations and the Hölder continuity of the de Rham functions

Published online by Cambridge University Press:  18 May 2009

Yibiao Pan
Yibiao Pan
Affiliation:
Department of Mathematics and Statistics, University of Pittsburgh, Pittsburgh, Pensylvania 15260, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use a simple approximation method to prove the Holder continuity of the generalized de Rham functions.

1. Consider the following dilatation equation

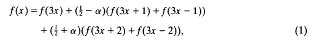
where |α|<l/2. Suppose that f is an integrable solution of (1); then f must satisfy

where 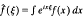is the Fourier transform of f, and

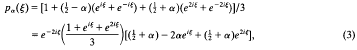
which immediately leads to

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 3 , September 1994 , pp. 309 - 311
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Daubechies, I. and Lagarias, J., Two-scale difference equations I. Existence and global regularity of solutions, SIAM J. Anal. 22 (1991), 1388–1410.CrossRefGoogle Scholar
2.I. Daubechies and J. Lagarias, Two-scale difference equations II. Local regularity, infinite product of matrices and fractals, to appear.Google Scholar