Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Clark, John
Tütüncü, Derya Keskin
and
Tribak, Rachid
2011.
Supplement Submodules of Injective Modules.
Communications in Algebra,
Vol. 39,
Issue. 11,
p.
4390.
Lee, Gangyong
Rizvi, S. Tariq
and
Roman, Cosmin S.
2011.
Dual Rickart Modules.
Communications in Algebra,
Vol. 39,
Issue. 11,
p.
4036.
Lee, Gangyong
Rizvi, S. Tariq
and
Roman, Cosmin S.
2012.
Direct sums of Rickart modules.
Journal of Algebra,
Vol. 353,
Issue. 1,
p.
62.
Kalati, T. Amouzegar
and
Tütüncü, D. Keskin
2013.
A note on noncosingular lifting modules.
Ukrainian Mathematical Journal,
Vol. 64,
Issue. 11,
p.
1776.
Lee, Gangyong
Rizvi, S. Tariq
and
Roman, Cosmin
2013.
Modules Whose Endomorphism Rings are Von Neumann Regular.
Communications in Algebra,
Vol. 41,
Issue. 11,
p.
4066.
Abyzov, A. N.
and
Nhan, T. H. N.
2014.
CS-Rickart modules.
Lobachevskii Journal of Mathematics,
Vol. 35,
Issue. 4,
p.
317.
Amouzegar, Tayyebeh
Keskin Tütüncü, Derya
and
Talebi, Yahya
2014.
t-Dual Baer Modules and t-Lifting Modules.
Vietnam Journal of Mathematics,
Vol. 42,
Issue. 2,
p.
159.
Abyzov, A. N.
2014.
I*0-Modules.
Russian Mathematics,
Vol. 58,
Issue. 8,
p.
1.
Tribak, Rachid
2015.
On Weak Dual Rickart Modules and Dual Baer Modules.
Communications in Algebra,
Vol. 43,
Issue. 8,
p.
3190.
Kalebog̃az, Berke
Keskin-Tütüncü, Derya
and
Smith, Patrick F.
2015.
Some Generalizations of Quasi-Projective Modules.
Algebra Colloquium,
Vol. 22,
Issue. spec01,
p.
727.
Le, Van Thuyet
and
Phan, Hong Tin
2016.
Some Characterizations of Modules via Essentially Small Submodules.
Kyungpook mathematical journal,
Vol. 56,
Issue. 4,
p.
1069.
Crivei, Septimiu
and
Kör, Arda
2016.
Rickart and Dual Rickart Objects in Abelian Categories.
Applied Categorical Structures,
Vol. 24,
Issue. 6,
p.
797.
Ghawi, Tha'ar Younis
2017.
On Closed Dual Rickart Modules.
Journal of Kufa for Mathematics and Computer,
Vol. 4,
Issue. 1,
p.
23.
Crivei, Septimiu
and
Olteanu, Gabriela
2018.
Strongly Rickart objects in abelian categories: Applications to strongly regular and strongly Baer objects.
Communications in Algebra,
Vol. 46,
Issue. 10,
p.
4426.
Crivei, Septimiu
and
Olteanu, Gabriela
2018.
Rickart and Dual Rickart Objects in Abelian Categories: Transfer via Functors.
Applied Categorical Structures,
Vol. 26,
Issue. 4,
p.
681.
Crivei, Septimiu
and
Keskin Tütüncü, Derya
2018.
Weak Rickart and dual weak Rickart objects in abelian categories.
Communications in Algebra,
Vol. 46,
Issue. 7,
p.
2912.
Crivei, Septimiu
and
Olteanu, Gabriela
2018.
Strongly Rickart objects in abelian categories.
Communications in Algebra,
Vol. 46,
Issue. 10,
p.
4326.
Pekacar Calci, Tugce
Harmanci, Abdullah
and
Ungor, Burcu
2019.
Generating dual Baer modules via fully invariant submodules.
Quaestiones Mathematicae,
Vol. 42,
Issue. 8,
p.
1125.
Tribak, R.
2020.
On a Class of Dual Rickart Modules.
Ukrainian Mathematical Journal,
Vol. 72,
Issue. 7,
p.
1118.
Crivei, Septimiu
Keskin Tütüncü, Derya
and
Tribak, Rachid
2020.
Transfer of splitness with respect to a fully invariant short exact sequence in abelian categories.
Communications in Algebra,
Vol. 48,
Issue. 6,
p.
2639.

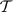 -non-cosingular modules, dual Baer modules and
-non-cosingular modules, dual Baer modules and 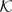 -modules. We prove that a module
-modules. We prove that a module 