Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T15:59:19.033Z Has data issue: false hasContentIssue false
  • English
  • Français

On Gordon's method of solving dual integral equations

Published online by Cambridge University Press:  18 May 2009

J. Burlak
J. Burlak
Affiliation:
North Carolina State College Raleigh, North Carolina, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Dual integral equations of the form

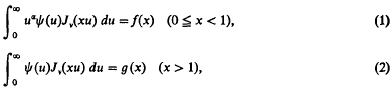
where f(x) and g(x) are given and Ψ(x) is the unknown, have been increasingly studied in recent years; the first solutions were given for the case g(x) ≡ 0 by Titchmarsh [1] (for 0 < α < 2) and Busbridge [2] (for — 2 < α < 0). An interesting and much simpler method of solving the equations in the same case, g ≡ 0, was given by Gordon [3]. He also showed that the problem of solving the general equations (1) and (2) can be reduced to a problem in which g ≡ 0. He did not pursue this idea as far as finding and simplifying the solution of (1) and (2) but this has been done recently (see [4]) and Noble [5] used a similar idea in treating the case f ≡ 0.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 3 , January 1964 , pp. 117 - 122
Copyright
Copyright © Glasgow Mathematical Journal Trust 1964

References

REFERENCES

1.Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Oxford, 1937), 334–339.Google Scholar
2.Busbridge, I. W., Dual integral equations, Proc. London Math. Soc. (2) 44 (1938), 115–129.CrossRefGoogle Scholar
3.Gordon, A. N., Dual integral equations, J. London Math. Soc. 29 (1954), 360–363.CrossRefGoogle Scholar
4.Burlak, J., On the solution of certain dual integral equations, Proc. Glasgow Math. Assoc. 6 (1963), 39–44.CrossRefGoogle Scholar
5.Noble, B., On some dual integral equations, Quart. J. Math. Oxford Ser. (2) 6 (1955), 81–87.CrossRefGoogle Scholar
6.Lowengrub, M. and Sneddon, I. N., On certain dual integral equations, U.S. Air Force Technical Report, Contract No. AF 49(638)–892,1961. [See also: The solution of a pair of dual integral equations, Proc. Glasgow Math. Assoc. 6 (1963), 14–18.]CrossRefGoogle Scholar
7.Copson, E. T., On certain dual integral equations, Proc. Glasgow Math. Assoc. 5 (1961), 21–24.CrossRefGoogle Scholar
8.Noble, B., Certain dual integral equations, J. Math. and Phys. 37 (1958), 128–136.CrossRefGoogle Scholar
9.Sneddon, I. N., Fourier Transforms (New York, 1951), p. 52.Google Scholar
10.Watson, G. N., A treatise on the theory of Bessel functions (Cambridge, 2nd edition, 1944).Google Scholar
11.Whittaker, E. T. and Watson, G. N., A course of modern analysis (Cambridge, 4th edition, 1927).Google Scholar
12.Peters, A. S., Certain dual integral equations and Sonine integrals (New York University, Research Report IMM-NYU 285, 08 1961).Google Scholar
13.Sneddon, I. N., Fractional integration and dual integral equations (North Carolina State College, 06 1962).CrossRefGoogle Scholar