No CrossRef data available.
Published online by Cambridge University Press: 18 May 2009
The classical theory of Weierstrass points on a compact Riemann surface is well-known (see, for example, [3]). Ogawa [6] has defined generalized Weierstrass points. Let Y denote a compact complex manifold of (complex) dimension n. Let E denote a holomorphic vector bundle on Y of rank q. Let Jk(E) (k = 0, 1, …) denote the holomorphic vector bundle of k-jets of E [2, p. 112]. Put rk(E) = rank Jk(E) = q.(n + k)!/n!k!. Suppose that Γ(E), the vector space of global holomorphic sections of E, is of dimension γ(E)>0. Consider the trivial bundle Y × Γ(E) and the map
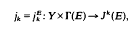
which at a point Q∈Y takes a section of E to its k-jet at Q. Put μ = min(γ(E),rk(E)).